Цепная линия

Цепна́я ли́ния, также катенария^[1], — линия, форму которой принимает гибкая однородная нерастяжимая тяжёлая нить или цепь (отсюда название линии) с закреплёнными концами в однородном гравитационном поле. Является плоской трансцендентной кривой.

Висящая цепь образует цепную линию

Цепная линия при различных значениях параметра ${\displaystyle a}$

Уравнение линии в декартовых координатах:

${\displaystyle y={\frac {a}{2}}(e^{x/a}+e^{-x/a})=a\operatorname {ch} {\frac {x}{a}}}$

(о функции ${\displaystyle \operatorname {ch} }$ см. гиперболический косинус).

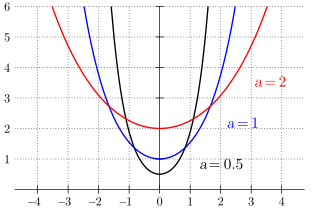
Все цепные линии подобны одна другой, изменение параметра ${\displaystyle a}$ эквивалентно равномерному растяжению или сжатию графика функции вдоль оси ${\displaystyle x}$. Переменная ${\displaystyle x}$ графика отсчитывается от самой низкой точки на оси ординат цепной линии. Значение этой ординаты равно значению ${\displaystyle a}$. Если значение параметра ${\displaystyle a}$ меньше нуля, то мы имеем не провисающую цепь, а арку.

Параметр ${\displaystyle a}$ имеет физический смысл. Это отношение горизонтальной проекции силы, растягивающей цепь, к удельному (линейному) весу цепи.

Математические свойства цепной линии впервые изучал Роберт Гук в 1670-х годах, а её уравнение было получено независимо Лейбницем, Гюйгенсом и Иоганном Бернулли в 1691 году.

Свойства

Натяжение цепной линии. Каждая кривая соответствует разному значению горизонтальной составляющей силы натяжения ${\displaystyle T_{H}.}$ Параметр ${\displaystyle a={\frac {T_{H}}{\lambda H}},}$ где ${\displaystyle \lambda }$ — погонная плотность нити

Цепная линия - траектория фокуса параболы, катящейся по прямой.

• Мыльная плёнка, натянутая на два параллельных кольца, не обязательно равных диаметров, принимает форму катеноида — поверхности, возникающей в результате вращения цепной линии.
• Длина дуги от вершины до произвольной точки ${\displaystyle (x,~y)}$:

  ${\displaystyle s=a\operatorname {sh} {\frac {x}{a}}={\sqrt {y^{2}-a^{2}}}.}$

• Радиус кривизны:

  ${\displaystyle R=a\operatorname {ch} ^{2}{\frac {x}{a}}={\frac {y^{2}}{a}}.}$

• Площадь, ограниченная цепной линией, двумя её ординатами и осью абсцисс:

  ${\displaystyle S=a^{2}\left(\operatorname {sh} {\frac {x_{2}}{a}}-\operatorname {sh} {\frac {x_{1}}{a}}\right)=a\left({\sqrt {y_{2}^{2}-a^{2}}}-{\sqrt {y_{1}^{2}-a^{2}}}\right).}$

• Траектория фокуса параболы, катящейся по прямой, есть цепная линия^[2][3].
• Центр тяжести цепной линии — самый низкий из всех форм нитей равной длины, соединяющих две опоры, т. е. имеет минимум потенциальной энергии^[4].

Применения

Арки

Перевёрнутая цепная линия — идеальная с точки зрения прочности форма для арок. Материал однородной арки с одинаковой по длине линейной плотностью в форме перевёрнутой цепной линии испытывает только механические напряжения сжатия и не испытывает напряжений изгиба.

Мосты

Горбатый мост имеет форму, близкую к цепной линии.

Стоит заметить, что форма изгиба тросов подвесного моста ближе к параболе, чем к цепной линии^[5]. Это связано с тем, что основной вес моста распределён в полотне моста, а не в поддерживающих тросах.

Трёхколёсный велосипед с квадратными колёсами едет по поверхности с профилем цепной линии

Квадратные колёса

Если профиль шоссе представляет собой перевёрнутые арки цепной линии, то по нему можно ездить на квадратных колёсах^[англ.], ровно и без тряски — если сторона квадрата колеса равна длине арки неровности дороги^[6][7].

История

Уравнение цепной линии практически одновременно получено Лейбницем, Гюйгенсом и Иоганном Бернулли^[8].

Дополнительные факты

На арке «Ворота на запад» в Сент-Луисе написана математическая формула её цепной линии, выраженная в футах^[9]:

${\displaystyle y=-127{,}7'\cdot \operatorname {ch} (x/127{,}7')+757{,}7'.}$

Выраженное в метрах, это уравнение будет ${\displaystyle y=-38{,}92\cdot \operatorname {ch} (x/38{,}92)+230{,}95.}$

См. также

• Фонтан из цепочки