Правильный четырнадцатиугольник

Четырнадцатиугольник (или тетрадекагон от греч. τετραδεκάγωνο) — это многоугольник с четырнадцатью сторонами.

Четырнадцатиугольник
Правильный четырнадцатиугольник
Тип	Правильный многоугольник
Рёбра	14
Символ Шлефли	{14}, t{7}
Диаграмма Коксетера — Дынкина
Вид симметрии	Диэдрическая группа (D14) порядок 2×14
Внутренний угол	примерно 154°
Свойства
выпуклый, вписанный, равносторонний, равноугольный[англ.], изотоксальный
Медиафайлы на Викискладе

Симметрия

Симметрии правильных четырнадцатиугольников. Вершины окрашены согласно их симметриям. Синие зеркала проведены через вершины, а фиолетовые — через середины сторон. Порядок группы вращений указан в центре фигуры.

Правильный четырнадцатиугольник имеет симметрию Dih₁₄ порядка 28. Имеется 3 подгруппы диэдральной симметрии: Dih₇, Dih₂, Dih₁, а также 4 циклических группы симметрии: Z₁₄, Z₇, Z₂, Z₁.

Справа на рисунке можно видеть 10 симметрий четырнадцатиугольника. Конвей использовал для обозначения симметрий буквы вместе с порядком группы^[1]. Полная симметрия правильной фигуры будет равна r28, а отсутствие симметрии отмечается как a1. Диэдральные симметрии делятся по тому, проходят они через вершины (используется буква d, от «diagonal») или через середины сторон (используется буква p, от «perpendicular»). Если же оси симметрии проходит через вершины и середины сторон, используется буква i. Циклические симметрии помечаются буквой g (от «gyration»). Каждая подгруппа симметрии допускает одну или более степеней свободы для неправильных форм. Только подгруппа g14 не даёт свободы, но стороны многоугольника могут рассматриваться как имеющие направление.

Правильный четырнадцатиугольник

Площадь правильного четырнадцатиугольника со стороной a задаётся формулой

${\displaystyle {\begin{aligned}A&={\frac {14}{4}}a^{2}\cot {\frac {\pi }{14}}={\frac {14}{4}}a^{2}\left({\frac {{\sqrt {7}}+4{\sqrt {7}}\cos \left({{\frac {2}{3}}\arctan {\frac {\sqrt {3}}{9}}}\right)}{3}}\right)\\&\simeq 15.33450193637188a^{2}\end{aligned}}}$

Построение четырнадцатиугольника

Правильный четырнадцатиугольник нельзя построить с помощью циркуля и линейки^[2]. Однако, его можно построить с помощью метода невсиса, если использовать его вместе с трисекцией угла,^[3] или с линейкой с метками^[4] как показано на следующих двух примерах.

Четырнадцатиугольник в заданной окружности:
Анимация (1м 47с) с помощью метода невсиса построения четырнадцатиугольника в окружности радиуса ${\displaystyle {\overline {OA}}=6}$, опираясь на трисекцию угла с помощью томагавка.

Четырнадцатиугольник с заданной длиной стороны:
Анимация (1м 20с) построения с помощью метода невсиса с применением маркированой линейки, согласно Дэвиду Джонсону Лейску (Крокетт Джонсону^[англ.])^[4]

Приблизительная конструкция четырнадцатиугольника.

Четырнадцатиугольники Петри

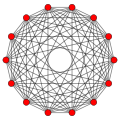
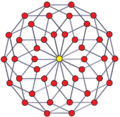
Пространственные четырнадцатиугольники существуют в виде многоугольников Петри для многих многогранников более высокой размерности. Примеры показаны в ортогональных проекциях:

• 
  Гептеракт
• 
  7-ортоплекс^[англ.]
• 
  7-7 дуопирамида^[англ.]
• 
  7-7 дуопризма
• 
  13-симплекс

Рассечение

По Коксетеру любой 2m-угольный зоногон можно разбить на m(m-1)/2 ромбов. Для правильного четырнадцатиугольника m=7 и его можно разбить на 21 ромб — на 3 набора по 7 ромбов. Это разбиение основано на проекции многоугольника Петри гептеракта с 21 из 672 граней^[5]. Список A006245 Архивная копия от 17 марта 2018 на Wayback Machine даёт число решений 24698, включая вращения и хиральные формы.

Разбиение на 21 ромб

В Малайзии

Флаг Малайзии.

Герб Малайзии.

Флаг вооружённых сил Малайзии.

Шаманский бубен "Сокол".

• В виде правильного 14-угольника чеканятся некоторые памятные золотые и серебряные малайзийские монеты. Число сторон в них символизирует число штатов Малайзийской Федерации.
• 14-лучевая звезда изображена на гербе Малайзии, её государственном флаге и флаге и эмблеме её вооружённых сил.

В традиционном искусстве

Шаманский этнический 14-угольный бубен, выполненный в германской традиции.^[6].

Четырнадцатиугольник также использовался в исламских декоративных узорах^[7].

Другое

Компьютерная игра Tetradecagon (Архивная копия от 21 февраля 2019 на Wayback Machine).

Абстрактный рисунок Momentia:Tetradecagon (Gaurav Bose, India)

В архитектуре: Glashouse (Bruno Taut, 1914)^[8]. Хор в форме четырнадцатиугольника в церкви св. Николая в Бари^[9]. Апсида церкви в Понтиньи (Архивная копия от 21 февраля 2019 на Wayback Machine) состоит из семи сторон четырнадцатиугольника и дополнительного полупролета.

Связанные фигуры

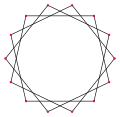
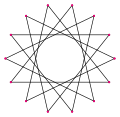
Четырнадцатиугольник имеет 14 сторон и представляется символом {14/n}. Имеется два правильных звёздчатых многоугольника — {14/3} и {14/5}, использующих те же самые вершины, но соединённые через три или через пять точек. Существует также три составных четырнадцатиугольника — {14/2} сводится к 2{7} (два семиугольника), а {14/4} и {14/6} сводятся к 2{7/2} и 2{7/3} (две различные гептаграммы), и, наконец, {14/7} сводится к семи двуугольникам.

Составные и звёздчатые многоугольники
n	1	2	3	4	5	6	7
Вид	Правильный	Составной	Звёздчатый	Составной	Звёздчатый	Составной
Рисунок	{14/1} = {14}	{14/2} = 2{7}	{14/3}	{14/4} = 2{7/2}	{14/5}	{14/6} = 2{7/3}	{14/7} or 7{2}
Внутренний угол	≈154.286°	≈128.571°	≈102.857°	≈77.1429°	≈51.4286°	≈25.7143°	0°

Более глубокие усечения правильного семиугольника и гептаграмм может дать изогональные (вершинно-транзитивные) промежуточные формы с равным расстоянием между вершинами и двумя длинами рёбер. Другие усечения могут дать многоугольники двойного накрытия 2{p/q}, а именно: t{7/6}={14/6}=2{7/3}, t{7/4}={14/4}=2{7/2} и t{7/2}={14/2}=2{7}^[10].

Изогональные усечения семиугольников и гептаграмм
Квазиправильный	Изогональный			Квазиправильный Двойное накрытие
t{7}={14}				{7/6}={14/6} =2{7/3}
t{7/3}={14/3}				t{7/4}={14/4} =2{7/2}
t{7/5}={14/5}				t{7/2}={14/2} =2{7}