E₈ (математика)

У этого термина существуют и другие значения, см. E8.

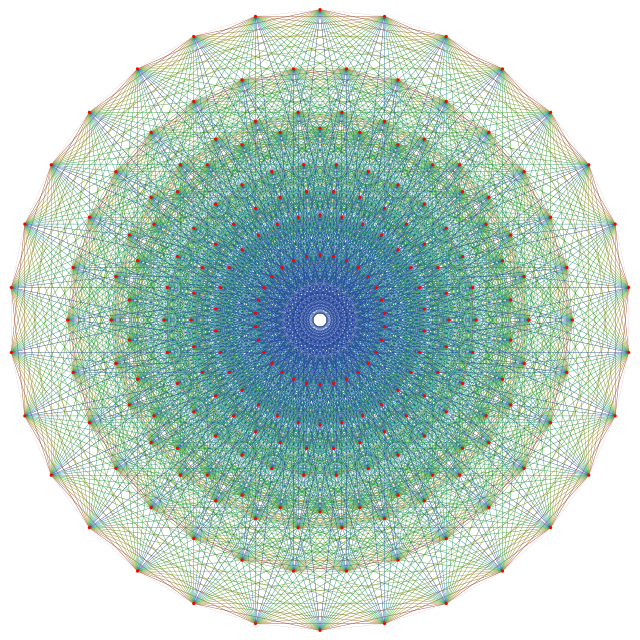
${\displaystyle E_{8}}$ — наибольшая особая простая группа Ли. ${\displaystyle E_{8}}$ была открыта Вильгельмом Киллингом в 1888—1890 годах, а современное её обозначение пришло из классификации простых алгебр Ли, которую ввели Эли Картан и Вильгельм Киллинг. Классификация выделяет четыре бесконечных семейства простых алгебр Ли, обозначаемых ${\displaystyle A_{n}}$, ${\displaystyle B_{n}}$, ${\displaystyle C_{n}}$, ${\displaystyle D_{n}}$, и пять особых случаев, обозначаемых E₆, E₇, E₈, F₄ и G₂.

Граф полиэдра ${\displaystyle \scriptstyle {E_{8}}}$

Описание

${\displaystyle E_{8}}$ имеет ранг 8 и размерность 248 (как многообразие). Векторы системы корней определены в восьми измерениях.

Схема Дынкина

Схема Дынкина для E₈ имеет вид

Эта схема вкратце описывает строение системы корней. Каждый узел схемы представляет собой простой корень. Линия, соединяющая два простых корня, означает, что они находятся под углом 120° друг к другу. Два простых корня, не соединённые линией, ортогональны.

Матрица Картана

Матрица Картана системы корней порядка r — это матрица ${\displaystyle r\times r}$, элементы которой определяются простыми корнями следующим образом:

${\displaystyle A_{ij}=2{\frac {(\alpha _{i},\alpha _{j})}{(\alpha _{i},\alpha _{i})}}}$

где ${\displaystyle (\cdot ,\cdot )}$ — евклидово скалярное произведение, а ${\displaystyle \alpha _{i}}$ — простые корни. Элементы матрицы не зависят от выбора простых корней (с точностью до порядка).

Матрица Картана для E₈ имеет вид

${\displaystyle \left[{\begin{smallmatrix}2&-1&0&0&0&0&0&0\\-1&2&-1&0&0&0&0&0\\0&-1&2&-1&0&0&0&-1\\0&0&-1&2&-1&0&0&0\\0&0&0&-1&2&-1&0&0\\0&0&0&0&-1&2&-1&0\\0&0&0&0&0&-1&2&0\\0&0&-1&0&0&0&0&2\end{smallmatrix}}\right]}$

Определитель этой матрицы равен 1.

См. также

• Решётка E₈
• E₈-многообразие
• Исключительно простая теория всего

Ссылки

• «Ну очень большой результат», Компьютерра, Галактион Андреев, 11 апреля 2007 года
• «В 248-мерное пространство прорвались теоретики», Cnews, 20 марта 2007 года