Heaviside function

The Heaviside function, often written as H(x), is a non-continuous function whose value is zero for a negative input and one for a positive input.

The Heaviside step function, using the half-maximum convention

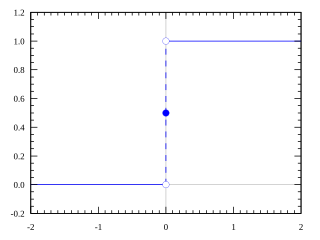
The function is used in the mathematics of control theory to represent a signal that switches on at a specified time, and which stays switched on indefinitely. It was named after the Englishman Oliver Heaviside.

The Heaviside function is the integral of the Dirac delta function: H′(x) = δ(x). This is sometimes written as^[1]

${\displaystyle H(x)=\int _{-\infty }^{x}{\delta (t)}\mathrm {d} t}$

Discrete form

We can also define an alternative form of the Heaviside step function as a function of a discrete variable n:

${\displaystyle H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}$

where n is an integer.

Or

${\displaystyle H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)}$

The discrete-time unit impulse is the first difference of the discrete-time step

${\displaystyle \delta \left[n\right]=H[n]-H[n-1].}$

This function is the cumulative summation of the Kronecker delta:

${\displaystyle H[n]=\sum _{k=-\infty }^{n}\delta [k]\,}$

where

${\displaystyle \delta [k]=\delta _{k,0}\,}$

is the discrete unit impulse function.

Representations

Often an integral representation of the Heaviside step function is useful:

${\displaystyle H(x)=\lim _{\epsilon \to 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau .}$

H(0)

The value of the function at 0 can be defined as H(0) = 0, H(0) = ½ or H(0) = 1. In particular:^[2]

${\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}}$

Related pages

• Laplace transform
• Step function