Rektifikacija (geometrija)

Rektifikacija je v geometriji postopek v katerem prisekamo politop tako, da označimo središčne točke vseh njegovih robov in odrežemo oglišča v teh točkah. Politop, ki nastane, je vezan na sliko oglišča in na odrezane facete izhodiščnega politopa.

Prisekana kocka je kubooktaeder – robovi so zmanjšani do ogliščin oglišča so razširjena do novih stranskih ploskev.

Birektificirana (dvojno rektificirana) kocka je oktaeder – stranske ploskve so zmanjšane v točke in nove stranske ploskve se nahajajo v prvotnih ogliščih.

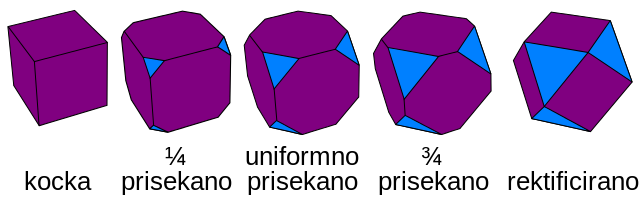
Zgled rektifikacije kot dokončno prisekanje

Rektifikacija je končni postopek pri prisekovanju. Na kocki to zaporedje kaže štiri korake med pravilno in rektificirano obliko

Rektifikacije višjega reda

Rektifikacije višjega reda se lahko izvedejo na pravilnih politopih z višjimi razsežnostmi. Najvišji red rektifikacije kreira dualne politope. Rektifikacija odreže robove tako, da postanejo točke. Birektifikacija odreže stranske ploskve tako, da te postanejo točke. Trirektifikacija odreže celice v točke in končna rektifikacija je dualni politop.

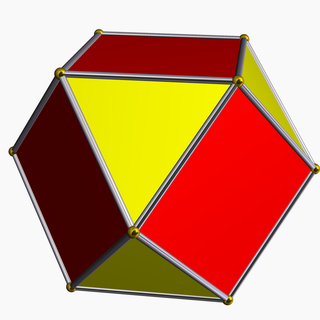
Primer birektifikacije kot končne prisekanosti

V mnogokotnikih

Dualni poligon je isto kot njegova rektificirana oblika.

V poliedrih in ravninskem tlakovanju

Vsako platonsko telo in njegov dual imajo isti rektificirani polieder.

Rektificirani polieder se kaže kot, da se lahko izrazi kot kombinacija imen izvornega telesa in njegovega duala

1. rektificiran tetraeder katerega dual je tetraeder se imenuje tetraeder, ki ga poznamo tudi kot oktaeder
2. rektificirani oktaeder, katerega dual je kocka, se imenuje kubooktaeder

družina	starševsko telo	rektifikacija	dualno telo
[3,3]	tetraeder	tetraeder	tetraeder
[4,3]	kocka	kubooktaeder	oktaeder
[5,3]	dodekaeder	ikozidodekaeder	ikozaeder
[6,3]	šestkotno tlakovanje	triheksagonalno tlakovanje	trikotno tlakovanje
[7,3]	heptagonalno tlakovanje reda 3	triheptagonalno tlakovanje	trikotno tlakovanje reda 7
[4,4]	kvadratno tlakovanje	kvadratno tlakovanje	kvadratno tlakovanje
[5,4]	pentagonalno tlakovanje reda 4	tetrapentagonalno tlakovanje	kvadratno tlakovanje reda 5

V nepravilnih poliedrih

Kadar polieder ni pravilen vedno niso srednje točke okoli oglišča v isti ravnini (koplanarne). Kljub temu je možna rektifikacija.

V polihoronih in v teselacijah trirazsežnega satovja

Vsak konveksni pravilni polihoronima rektificirano obliko uniformnega polihorona.

Pravilni polihoron {p, q, r} ima celice {p, q} dveh vrst rektificirane {p, q}, ki so ostale od izvornih celic in novih celic {q, r} poliedra, ki so nastale v vsakem od prirezanih oglišč.

Zgledi:

družina	starševsko telo	rektifikacija	Birektifikacija (dualna rektifikacija)	Trirektifikacija (dualna)
[3,3,3]	5-celica	rektificirana 5-celica	rektificirana 5-celica	5-celica
[4,3,3]	teserakt	rektificirani teserakt	rektificirana 16-celica (24-celica)	16-celica
[3,4,3]	24-celica	rektificirana 24-celica	rektificirana 24-celica	24-celica
[5,3,3]	120-celica	rectificirana 120-celica	rektificirana 600-celica	600-celica
[4,3,4]	kubično satovje	(Ni slike) rektificirano kubično satovje	(Ni slike) rektificirano kubično satovje	kubično satovje
[5,3,4]	Order-4 dodecahedral	(Ni slike) rektificirano dodekaedersko satovje reda 4	(Ni slike) rektificirano kubično satovje reda 5	kubično satovje reda 5

Red rektifikacije

Prvi red rektifikacije odreže robove do točk. Kadar je politop pravilni politop lahko njegovo obliko prikažemo z razširjenim Schläflijevim simbolom, ki ima obliko t₁{p,q,...}.

Rektifikacija drugega reda se imenuje birektifikacija. Če je pravilna, jo označujemo s t₂{p,q,...}.

Pri poliedrih birektifikacija naredi dualne poliedre.

Rektifikacije višjega reda se lahko konstruirajo za politope višjega reda. V splošnem n-rektifikacija odreže n-stransko ploskev do točk.

Kadar n-politop rektificiramo, se njegove facete zmanšajo v točke in politop, ki ga dobimo, je njegov dual.

Notacije in facete

Pravilni mnogokotniki

Facete so robovi, ki jih označujemo z {2}.

name {p}	Coxeter-Dinkin	t-notacija Schläflijev simbol	navpični Schläflijev simbol
			ime	faceta-1	faceta-2
starševski		t0{p}	${\displaystyle {\begin{Bmatrix}p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}2\end{Bmatrix}}}$
rektificirano		t1{p}	${\displaystyle {\begin{Bmatrix}p\end{Bmatrix}}}$		${\displaystyle {\begin{Bmatrix}2\end{Bmatrix}}}$

Pravilni poliedri in tlakovanja

Facete so pravilni mnogokotniki.

name {p,q}	Coxeter-Dinkin	t-notation Schläflijev simbol	navpični Schläflijev simbol
			ime	faceta-1	faceta-2
starševski		t0{p,q}	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\end{Bmatrix}}}$
rektificirani		t1{p,q}	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q\end{Bmatrix}}}$
birektificirani		t2{p,q}	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$		${\displaystyle {\begin{Bmatrix}q\end{Bmatrix}}}$

Pravilni polihoroni in satovje

Facete so pravilni ali rektificirani poliedri.

name {p,q,r}	Coxeter-Dinkin	t-notation Schläflijev simbol	navpični Schläflijev simbol
			ime	faceta-1	faceta-2
starševski		t0{p,q,r}	${\displaystyle {\begin{Bmatrix}p,q,r\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$
rektificirani		t1{p,q,r}	${\displaystyle {\begin{Bmatrix}p\ \ \\q,r\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q,r\end{Bmatrix}}}$
birektificirani		t2{p,q,r}	${\displaystyle {\begin{Bmatrix}q,p\\r\ \ \end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q\\r\end{Bmatrix}}}$
trirektificirani		t3{p,q,r}	${\displaystyle {\begin{Bmatrix}r,q,p\end{Bmatrix}}}$		${\displaystyle {\begin{Bmatrix}r,q\end{Bmatrix}}}$

Pravilni 5-politopi (politoroni) in 4-razsežno satovje

Facete so pravilni ali rektificirani polihoroni.

name {p,q,r,s}	Coxeter-Dinkin	t-notation Schläflijev simbol	navpični Schläflijev simbol
			ime	faceta-1	faceta-2
Parent		t0{p,q,r,s}	${\displaystyle {\begin{Bmatrix}p,q,r,s\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p,q,r\end{Bmatrix}}}$
rektificirani		t1{p,q,r,s}	${\displaystyle {\begin{Bmatrix}p\ \ \ \ \ \\q,r,s\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\ \ \\q,r\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q,r,s\end{Bmatrix}}}$
birektificirani		t2{p,q,r,s}	${\displaystyle {\begin{Bmatrix}q,p\\r,s\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q,p\\r\ \ \end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q\ \ \\r,s\end{Bmatrix}}}$
trirektificirani		t3{p,q,r,s}	${\displaystyle {\begin{Bmatrix}r,q,p\\s\ \ \ \ \ \end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}r,q,p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}r,q\\s\ \ \end{Bmatrix}}}$
kvadrirektificirani		t4{p,q,r,s}	${\displaystyle {\begin{Bmatrix}s,r,q,p\end{Bmatrix}}}$		${\displaystyle {\begin{Bmatrix}s,r,q\end{Bmatrix}}}$

Glej tudi

• dualni politop
• kvazipravilni polieder
• prisekanost (geometrija)
• Conwayjeva notacija poliedrov
• seznam pravilnih politopov
• kantelacija (geometrija)

Zunanje povezave

• Rektifikacija na MathWorld (angleško)
• Rektifikacija v Glossary for Hyperspace (angleško)