Parabola

Në matematikë, një parabolë është një kurbë e rrafshët e cila është simetrike sipas një boshti dhe është afërsisht në formë U-je. Parabola përshtatet me disa përshkrime matematikore sipërfaqësisht të ndryshme, të cilat të gjitha mund të vërtetohet se përcaktojnë saktësisht të njëjtat kurba.

Parabola është një anëtar i familjes së seksioneve konike .Me rradhë nga lart-poshtë: rrethi, elipsi, parabola dhe hiperbola

Një përshkrim i një parabole përfshin një pikë ( vatrën ) dhe një vijë ( vijën drejtuese ). Vatra nuk shtrihet në vijën drejtuese. Parabola është vendndodhja e pikave në atë rrafsh që janë të baraslarguara si nga vija drejtuese ashtu edhe nga fokusi. Një përshkrim tjetër i një parabole është si një prerje konike, i krijuar nga prerja e një sipërfaqeje konike rrethore të djathtë dhe një rrafshi paralel me një plan tjetër që është tangent me sipërfaqen konike. ^[a]

Parabolat gëzojnë vetinë që, nëse janë prej një materiali që reflekton dritën, atëherë rrezet e dritës që bien paralelisht me boshtin e simetrisë së parabolës dhe godet anën e saj të lugët (konkave), reflektohet në vatrën e saj, pavarësisht pikës së reflektimit . Në të kundërt, drita që del nga një burim pikësor në vatër reflektohet në një rreze paralele (" të përafërt "), duke e lënë parabolën paralele me boshtin e simetrisë. Të njëjtat efekte ndodhin me zërin dhe valët e tjera. Kjo veti reflektuese është baza e shumë përdorimeve praktike të parabolave.

Parabola ka shumë zbatime të rëndësishme, nga një antenë parabolike ose mikrofon parabolik te reflektorët e fenerëve të automobilave dhe dizajni i raketave balistike . Përdoret shpesh në fizikë, inxhinieri dhe shumë fusha të tjera.

Historia

Busulla parabolike e projektuar nga Leonardo da Vinci

Puna më e hershme e njohur mbi prerjet konike ishte nga Menaechmus në shekullin e IV para Krishtit. Ai zbuloi një mënyrë për të zgjidhur problemin e dyfishimit të kubit duke përdorur parabola. (Sidoqoftë, zgjidhja nuk i plotëson kërkesat e ndërtimit me kompas dhe vizore . ) Zona e kufizuar nga një parabolë dhe një segment vije, i ashtuquajturi "segment i parabolës", u llogarit nga Arkimedi me metodën e shterimit në shekullin e 3 para Krishtit, në "Kuadratura e Parabolës" . Emri "parabolë" i detyrohet Apollonit, i cili zbuloi shumë veti të prerjeve konike. Do të thotë "zbatim", duke iu referuar konceptit "zbatim i zonave", që ka një lidhje me këtë kurbë, siç e kishte vërtetuar Apolloni. ^[1] Vetia vatër-drejtuese e parabolës dhe prerjeve të tjera konike i detyrohet Papit.

Galileo tregoi se rruga e një predhe ndjek një parabolë, pasojë e nxitimit të njëtrajtshëm për shkak të gravitetit.

Mendimi se një reflektor parabolik mund të prodhojë një imazh ishte tashmë i njohur përpara shpikjes së teleskopit reflektues . ^[2] Projektime u propozuan në fillim të mesit të shekullit të 17-të nga shumë matematikanë, duke përfshirë Rëne Dekartin, Marin Mersenne, ^[3] dhe James Gregory . ^[4] Kur Isak Njutoni ndërtoi teleskopin e parë reflektues në 1668, ai nuk përdori një pasqyrë parabolike për shkak të vështirësisë së prodhimit, duke zgjedhur një pasqyrë sferike . Pasqyrat parabolike përdoren në shumicën e teleskopëve reflektues modernë dhe në pjatat satelitore dhe marrësit e radarëve . ^[5]

Përkufizimi si një grumbull pikash

Një parabolë mund të përkufizohet gjeometrikisht si një grup pikash ( lokus pikash) në rrafshin Euklidian:

• Një parabolë është një grup pikash, të tilla që për çdo pikë ${\displaystyle P}$ të vendosur në largësinë ${\displaystyle |PF|}$ në një pikë fikse ${\displaystyle F}$, vatra, është i barabartë me distancën ${\displaystyle |Pl|}$ në një linjë fikse ${\displaystyle l}$, drejtimi :

${\displaystyle \{P:|PF|=|Pl|\}.}$

Pika e mesit ${\displaystyle V}$ e pingules nga vatra ${\displaystyle F}$ mbi vijën drejtuese ${\displaystyle l}$ quhet kulm, dhe drejtëza ${\displaystyle FV}$ është boshti i simetrisë së parabolës.

Në një sistem koordinativ kartezian

Boshti i simetrisë paralel me boshtin y

Parabola me bosht paralel me boshtin y ;

Në terma të koordinatave karteziane, të tilla që ${\displaystyle F=(0,f),\ f>0,}$ dhe vija drejtuese ka ekuacionin ${\displaystyle y=-f}$, fitohet për një pikë ${\displaystyle P=(x,y)}$ nga relacioni i përkufizimit ekuacioni${\displaystyle x^{2}+(y-f)^{2}=(y+f)^{2}}$ . Zgjidhja sipas ${\displaystyle y}$ jep:

${\displaystyle y={\frac {1}{4f}}x^{2}.}$

Korda horizontale përmes vatrës (shih foton në seksionin hapës) quhet latus rectum ; gjysma e saj emërtohet semi-latus rectum . Latus rectum është paralel me vijën drejtuese. Semi-lactus rectum shënohet me shkronjë ${\displaystyle p}$ . Nga skica merret

${\displaystyle p=2f.}$

Latus rectum është përcaktuar në mënyrë të ngjashme për dy koniket e tjera - elipsin dhe hiperbolën. Latus rectum është vija e tërhequr përmes një vatre të një prerje konik paralel me drejtuesen dhe që përfundon në të dyja drejtimet nga kurba. Për çdo rast, ${\displaystyle p}$ është rrezja e rrethit shallës në kulm. Për një parabolë, ${\displaystyle p}$, është largësia e vatrës nga drejtuesja. Duke përdorur parametrin ${\displaystyle p}$, ekuacioni i parabolës mund të rishkruhet në formën:

${\displaystyle x^{2}=2py.}$

Ky njihet edhe si ekuacioni standard i parabolës.

Parabola e çfarëdoshme

Parabola e çfarëdoshme

Nëse vatra ka koordinata ${\displaystyle F=(f_{1},f_{2})}$, dhe vija drejtuese ka ekuacion ${\displaystyle ax+by+c=0}$, atëherë fitohet ekuacioni

${\displaystyle {\frac {(ax+by+c)^{2}}{a^{2}+b^{2}}}=(x-f_{1})^{2}+(y-f_{2})^{2}}$

Ekuacioni i nënkuptuar i një parabole përcaktohet nga një polinom i pareduktueshëm i shkallës së dytë:

${\displaystyle ax^{2}+bxy+cy^{2}+dx+ey+f=0,}$

Si grafik i një funksioni

Parabolat ${\displaystyle y=ax^{2}}$

Seksioni i mëparshëm tregon se çdo parabolë me origjinën si kulm dhe boshtin y si bosht simetrie mund të konsiderohet si grafiku i një funksioni

${\displaystyle f(x)=ax^{2}{\text{ with }}a\neq 0.}$

Për ${\displaystyle a>0}$ parabolat janë me kokë lart, dhe për ${\displaystyle a<0}$ janë me kokë poshtë. Nga seksioni i mësipërm fitohet:

• Vatra është ${\displaystyle \left(0,{\frac {1}{4a}}\right)}$ ,
• gjatësia vatrore ${\displaystyle {\frac {1}{4a}}}$, parametri ${\displaystyle p={\frac {1}{2a}}}$ ,
• kulmi është ${\displaystyle (0,0)}$ ,
• vija drejtuese ka ekuacionin ${\displaystyle y=-{\frac {1}{4a}}}$ ,
• tangjentja në pikë ${\displaystyle (x_{0},ax_{0}^{2})}$ ka ekuacionin ${\displaystyle y=2ax_{0}x-ax_{0}^{2}}$ .

Për ${\displaystyle a=1}$ parabola është parabola njësi me ekuacion ${\displaystyle y=x^{2}}$ . Vatra e saj është në pikën me koordinatë ${\displaystyle \left(0,{\tfrac {1}{4}}\right)}$, parametri ${\displaystyle p={\tfrac {1}{2}}}$, dhe vija drejtuese ka ekuacionin ${\displaystyle y=-{\tfrac {1}{4}}}$ .

Funksioni i përgjithshëm i shkallës së dytë është

${\displaystyle f(x)=ax^{2}+bx+c{\text{ ku }}a,b,c\in \mathbb {R} ,\ a\neq 0}$ .

Plotësimi i katrorit jep

${\displaystyle f(x)=a\left(x+{\frac {b}{2a}}\right)^{2}+{\frac {4ac-b^{2}}{4a}},}$

i cili është ekuacioni i një parabole me

• boshtin ${\displaystyle x=-{\frac {b}{2a}}}$ (paralel me boshtin y ),
• gjatësinë vatrore ${\displaystyle {\frac {1}{4a}}}$, parametrin ${\displaystyle p={\frac {1}{2a}}}$ ,
• kulmin ${\displaystyle V=\left(-{\frac {b}{2a}},{\frac {4ac-b^{2}}{4a}}\right)}$ ,
• vatrën ${\displaystyle F=\left(-{\frac {b}{2a}},{\frac {4ac-b^{2}+1}{4a}}\right)}$ ,
• vijën drejtuese ${\displaystyle y={\frac {4ac-b^{2}-1}{4a}}}$ ,
• pikën e parabolës që pret boshtin y në koordinatën ${\displaystyle (0,c)}$ ,
• tangjentja në një pikë të boshtit y ka ekuacionin ${\displaystyle y=bx+c}$ .

Si një prerje konike e veçantë

Llojet e konikeve me një kulm të përbashkët

Lapsi i prerjeve konike me boshtin x si bosht simetrie, një kulm në origjinë (0, 0) dhe i njëjti parametër ${\displaystyle p}$ mund të përfaqësohet nga ekuacioni

${\displaystyle y^{2}=2px+(e^{2}-1)x^{2},\quad e\geq 0,}$

me jashtëqendërsinë ${\displaystyle e}$ .

• Për ${\displaystyle e=0}$ konikja është një rreth (rrethi oskulues i lapsit),
• për ${\displaystyle 0<e<1}$ një elips ,
• për ${\displaystyle e=1}$ parabola me ekuacion ${\displaystyle y^{2}=2px,}$
• për ${\displaystyle e>1}$ një hiperbolë (shih foton).

Në koordinatat polare

Lapsi i konikeve me fokus të përbashkët

Nëse p > 0, parabola me ekuacion ${\displaystyle y^{2}=2px}$ (hapja në të djathtë) ka paraqitjen polare

${\displaystyle r=2p{\frac {\cos \varphi }{\sin ^{2}\varphi }},\quad \varphi \in \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]\setminus \{0\}}$

( ${\displaystyle r^{2}=x^{2}+y^{2},\ x=r\cos \varphi }$ ).

Kulmi i saj është ${\displaystyle V=(0,0)}$, dhe vatra e saj është ${\displaystyle F=\left({\tfrac {p}{2}},0\right)}$ .

Nëse merret origjina si vatër, d.m.th. ${\displaystyle F=(0,0)}$, fitohet ekuacioni

${\displaystyle r={\frac {p}{1-\cos \varphi }},\quad \varphi \neq 2\pi k.}$

Fakte që lidhen me kordat dhe harqet

Zona e kufizuar nga një parabolë dhe një hark

Parabola (ngjyrë magenta) dhe vija (e ulët blu e lehtë) duke përfshirë një hark (blu). Zona e mbyllur mes tyre është në ngjyrë rozë. Vetë korda përfundon në pikat ku vija kryqëzon parabolën.

Zona e mbyllur midis një parabole dhe një korde (shih diagramin) është e barabartë me dy të tretat e sipërfaqes së një paralelogrami që e rrethon atë. Njëra anë e paralelogramit është korda, dhe ana e kundërt është një tangjente me parabolën. ^{[6] [7]} Pjerrësia e anëve të tjera paralele është e parëndësishme për zonën.

Nëse korda ka gjatësi b dhe është pingul me boshtin e simetrisë së parabolës, dhe nëse largësia pingule nga kulmi i parabolës me kordën është h, paralelogrami është një drejtkëndësh, me brinjë b dhe h . Zona S e segmentit parabolik e kufizuar nga parabola dhe korda është pra

${\displaystyle S={\frac {2}{3}}bh.}$

Në përgjithësi, zona e mbyllur mund të llogaritet si më poshtë. Së pari, gjeni pikën në parabolë ku pjerrësia e saj është e barabartë me atë të kordës. Kjo mund të bëhet me anë të metodave të analizës, ose duke përdorur një vijë që është paralele me boshtin e simetrisë së parabolës dhe kalon nga mesi i kordës. Pika e kërkuar është vendi ku kjo drejtëz kryqëzon parabolën. ^[b] Më pas, duke përdorur formulën e dhënë në Largësia e një pike nga një vijë, llogarisni largësinë pingule nga kjo pikë deri te korda. Shumëzojeni këtë me gjatësinë e kordës për të marrë sipërfaqen e paralelogramit, pastaj me 2/3 për të marrë zonën e mbyllur.

Gjatësia e harkut

Nëse një pikë X ndodhet në një parabolë me gjatësi vatrore f , dhe nëse p është largësia pingule nga X në boshtin e simetrisë së parabolës, atëherë gjatësitë e harqeve të parabolës që përfundojnë në X mund të llogariten nga f dhe p si më poshtë, duke supozuar se të gjitha janë të shprehura në të njëjtat njësi. ^[c]

${\displaystyle {\begin{aligned}h&={\frac {p}{2}},\\q&={\sqrt {f^{2}+h^{2}}},\\s&={\frac {hq}{f}}+f\ln {\frac {h+q}{f}}.\end{aligned}}}$

Madhësia s është gjatësia e harkut ndërmjet X dhe kulmit të parabolës.

Gjatësia e harkut ndërmjet X dhe pikës simetrikisht të kundërt në anën tjetër të parabolës është 2s .

Largësisë pingule p mund t'i jepet një shenjë pozitive ose negative për të treguar se në cilën anë të boshtit të simetrisë ndodhet pika X. Ndërrimi i shenjës së p-së përmbys shenjat e h-së dhe s-së pa ndryshuar vlerat e tyre absolute. Nëse këto madhësi janë me shenjë, gjatësia e harkut ndërmjet çdo dy pikash në parabolë jepet gjithmonë nga diferenca midis vlerave të tyre të s . Llogaritja mund të thjeshtohet duke përdorur vetitë e logaritmeve:

${\displaystyle s_{1}-s_{2}={\frac {h_{1}q_{1}-h_{2}q_{2}}{f}}+f\ln {\frac {h_{1}+q_{1}}{h_{2}+q_{2}}}.}$

Kjo mund të jetë e dobishme, për shembull, në llogaritjen e madhësisë së materialit të nevojshëm për të bërë një reflektor parabolik ose një lug parabolik .

Integrimi numerik

Rregulla e Simpsonit: grafiku i një funksioni zëvendësohet nga një hark i një parabole

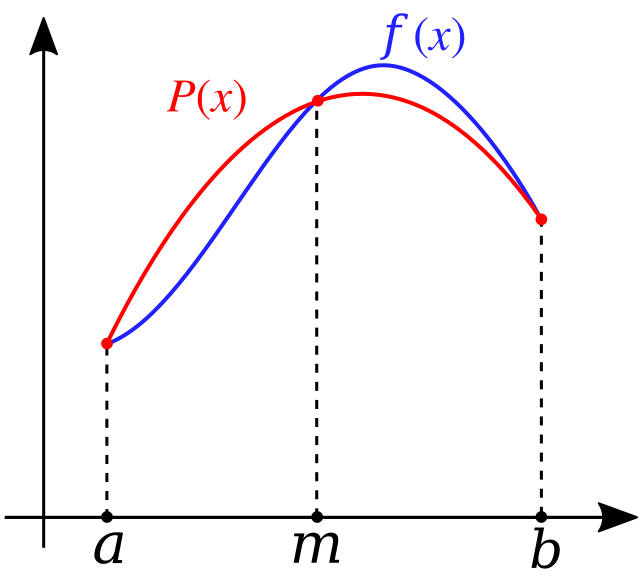
Në një metodë të integrimit numerik, grafiku i një funksioni zëvendësohet me harqe parabolash dhe integron harqet e parabolës. Një parabolë përcaktohet nga tre pika. Formula për një hark është

${\displaystyle \int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{6}}\cdot \left(f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right).}$

Metoda quhet rregulla e Simpsonit .