Трапез (геометрија)

Трапез преусмерава овде. За друга значења погледајте страницу Трапез (вишезначна одредница).

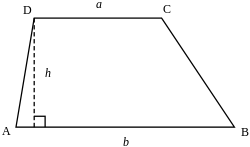
У Еуклидовој геометрији, трапез је конвексни четвороугао са најмање једним паром паралелних страница.^[1][2] Паралелне странице се зову основице трапеза, а друге две странице се зову краци или бочне странице (ако нису паралелне, онда постоје два пара основица). Скаленски трапез је трапез без икаквих страница са једнаким мерама,^[3] за разлику од посебних случајева испод.

Трапез
Трапез
Тип	четвороугао
Ивице и темена	4
Површина	${\displaystyle {\tfrac {a+b}{2}}h}$
Својства	конвексан

Висина трапеза је растојање између две паралелне странице. Збир углова на једном од кракова је 180° тј. α + δ = β + γ = 180°.

Етимологија трапез vs трапезоид

Хатонова грешка 1795.^[4]

Старогрчки математичар Еуклид дефинисао је пет типова четвороугла, од којих су четири имала два скупа паралелних страница (познате као квадрат, правоугаоник, ромб и ромбоид), и последњи који није имао два скупа паралелних страница – τραπέζια (trapezia^[5] дословно „сто“, сам од τετράς (tetrás), „четири“ + πέζα (péza), „стопало; крај, граница, ивица“).^[6]

Две врсте трапеза је увео Прокло (412. до 485. године) у свом коментару на прву књигу Еуклидових елемената:^[4][7]

• један пар паралелних страница – трапез (τραπέζιον), подељен на једнакокраке (једнаке ноге) и скалене (неједнаке) трапезе
• нема паралелних страница – трапезоид (τραπεζοειδή, trapezoeidé, дословно налик трапезу (εἶδος значи „наликује“), на исти начин као што кубоидни значи коцкасти, а ромбоидни значи попут ромба)

Сви европски језици прате Проклову структуру^[7][8] као и енглески до касног 18. века, све док утицајни математички речник који је објавио Чарлс Хатон 1795. није подржао без објашњења транспозицију термина. Ова грешка је исправљена на британском енглеском око 1875. године, али је задржана у америчком енглеском до данашњег дана.^[4]

Тип	Слика	Оригинална терминологија			Савремена терминологија
		Еуклид (Дефиниција 22)	Прокло (Дефиниције 30-34, цитирајући Посидонија)	Еуклид / Проклова дефиниција	Британски енглески (и европски језици)	Амерички енглески
Паралелограм		ῥόμβος (ромбови)		једнакостранични, али не правоугли	Ромб		Трапезоид (инклузивно)
		ῥομβοειδὲς (ромбоиди)		супротне стране и углови једнаки су једни другима, али не једнакостранични нити правоугли ромбоид	Ромбоид (колоквијално паралелограм)
Непараллелограм		τραπέζια (трапезија)	τραπέζιον ἰσοσκελὲς (трапезион isoskelés)	Две паралелне странице и линија симетрије	Изосилни трапезијум	Изосилни трапезоид
			τραπέζιον σκαληνὸν (трапезион skalinón)	Две паралелне странице, без линије симетрије	Трапезијум	Трапезоид (ексклузивно)
			τραπέζοειδὲς (трапезоиди)	Нема паралелних страница	Трапезоид	Трапезијум

Облик се често назива неправилан четвороугао.^[9][10]

Инклузивна наспрам ексклузивне дефиниције

Постоје одређена неслагања да ли паралелограме, који имају два пара паралелних страница, треба сматрати трапезоидима. Неки дефинишу трапез као четвороугао који има само један пар паралелних страница (ексклузивна дефиниција), чиме се искључују паралелограми.^[11] Други^[12] дефинишу трапез као четвороугао са најмање једним паром паралелних страница (инклузивна дефиниција^[13]), чинећи паралелограм посебним типом трапеза. Последња дефиниција је у складу са њеном употребом у вишој математици као што је калкулус. Овај чланак користи инклузивну дефиницију и разматра паралелограме као посебне случајеве трапеза. Ово се заговара и у таксономији четвороуглова.

Посебни случајеви

Посебни случајеви трапеза су:

• једнакокраки трапез, код кога су краци једнаки, такође и углови на основици су једнаки
• правоугли трапез, код кога је један крак управан на базу, тада је тај крак истовремено и висина
• паралелограм, код кога је и други пар страница међусобно паралелан
• ромб, који је паралелограм, али су му и све странице међусобно једнаке
• правоугаоник, који је паралелограм, али су му и све суседне странице међусобно нормалне
• квадрат, коме су све странице међусобно једнаке, а суседне међусобно нормалне

Услов постојања

Четири дужине a, c, b, d могу чинити узастопне странице непаралелограмског трапеза са a и b паралелним само када^[14]

${\displaystyle \displaystyle |d-c|<|b-a|<d+c.}$

Четвороугао је паралелограм када је ${\displaystyle d-c=b-a=0}$, али је екстангенцијални четвороугао (који није трапез) када је ${\displaystyle |d-c|=|b-a|\neq 0}$.^{[15]‍:p. 35}

Карактеризације

Општи трапезоид/трапез:
паралелне странице: ${\displaystyle a,\,b}$ са ${\displaystyle a<b}$
ноге: ${\displaystyle c,\,d}$
дијагонале: ${\displaystyle q,\,p}$
средњи сегмент: ${\displaystyle m}$
висина/алтитуда: ${\displaystyle h}$

Трапезоид/трапез са супротним троугловима ${\displaystyle S,\,T}$ формираним од дијагонала

За дати конвексни четвороугао, следећа својства су еквивалентна, а свако имплицира да је четвороугао трапезоид:

• Има два суседна угла која су суплементарна, односно сабирају до 180 степени.
• Угао између странице и дијагонале једнак је углу између супротне стране и исте дијагонале.
• Дијагонале секу једна другу у међусобно истом односу (овај однос је исти као и између дужина паралелних страница).
• Дијагонале секу четвороугао на четири троугла од којих један супротни пар има једнаке површине.^{[15]‍:Prop.5}
• Производ површина два троугла које формира једна дијагонала једнак је производу површина два троугла која формира друга дијагонала.^{[15]‍:Thm.6}
• Површине S и T неких од два супротна троугла међу четири троугла формирана дијагоналама задовољавају једначину

${\displaystyle {\sqrt {K}}={\sqrt {S}}+{\sqrt {T}},}$

где је K површина четвороугла.^{[15]‍:Thm.8}

• Средина две супротне стране и пресек дијагонала су колинеарни.^{[15]‍:Thm.15}
• Углови у четвороуглу ABCD задовољавају ${\displaystyle \sin A\sin C=\sin B\sin D.}$^{[15]‍:p. 25}
• Косинуси два суседна угла су 0, као и косинуси друга два угла.^{[15]‍:Thm.15}
• Котангенси два суседна угла су збир 0, као и котангенси друга два суседна угла.^{[15]‍:p. 26}
• Један бимедијан дели четвороугао на два четвороугла једнаких површина.^{[15]‍:p. 26}
• Двострука дужина бимедијана која повезује средине две супротне стране једнака је збиру дужина других страница.^{[15]‍:p. 31}

Поред тога, следећа својства су еквивалентна и свако имплицира да су супротне стране a и b паралелне:

• Узастопне странице a, c, b, d и дијагонале p, q задовољавају једначину^{[15]‍:Cor.11}

${\displaystyle p^{2}+q^{2}=c^{2}+d^{2}+2ab.}$

• Растојање v између средина дијагонала задовољава једначину^{[15]‍:Thm.12}

${\displaystyle v={\frac {|a-b|}{2}}.}$

Формуле

Обим	${\displaystyle O=a+b+c+d\,}$
Висина	${\displaystyle h=b\sin {\beta }=d\sin {\alpha }\,}$ ${\displaystyle h\,=\,{\frac {2}{a-c}}{\sqrt {s(s-(a-c))(s-b)(s-d)}},\;s\,=\,{\frac {a+c+b+d}{2}}}$
Површина	${\displaystyle P\,=\,{\frac {a+b}{2}}\cdot h}$
Дијагонале	${\displaystyle d_{1}\,=\,{\sqrt {a^{2}+b^{2}-2\,a\,b\,\cos \beta }}={\sqrt {c^{2}+d^{2}-2\,c\,d\,\cos \delta }}}$ ${\displaystyle d_{2}\,=\,{\sqrt {a^{2}+d^{2}-2\,a\,d\,\cos \alpha }}={\sqrt {b^{2}+c^{2}-2\,b\,c\,\cos \gamma }}}$

Једнакокраки трапез

Код једнакокраког трапеза важи да је = , такође је α = β одакле следи δ = γ. Последица овога је да је збир наспрамних углова α + γ = β + δ = 180°. Ово је особина тетивних четвороуглова, значи једнакокраки трапез је тетивни четвороугао.

Правоугли трапез

Код правоуглог трапеза је или једнако , а такође важи да је α = δ = 90° ili β = γ = 90°.