பிரம்மகுப்தரின் வாய்பாடு

யூக்ளீடிய வடிவவியலில் பிரம்மகுப்தரின் வாய்ப்பாடு என்பது (Brahmagupta's formula) வட்ட நாற்கரத்தின் பரப்பளவு காணும் வாய்ப்பாடு ஆகும். ஒரு வட்ட நாற்கரத்தின் பக்கங்களின் நீளங்கள் தரப்பட்டிருக்கும் போது இவ்வாய்ப்பாட்டைப் பயன்படுத்தி அந்த வட்ட நாற்கரத்தின் பரப்பைக் காணலாம்.

அடிப்படைப் படிவம்

பிரம்மகுப்தரின் வாய்ப்பாட்டின் எளிமையானதும் எளிதில் மனதில் பதியக்கூடியதுமான படிவம், a, b, c, d -ஐ பக்க நீளங்களாகக் கொண்ட வட்ட நாற்கரத்தின் பரப்பைத் தருகிறது:

${\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}$

இங்கு s, நாற்கரத்தின் அரைச்சுற்றளவு.

${\displaystyle s={\frac {a+b+c+d}{2}}\cdot }$

${\displaystyle s-a={\frac {-a+b+c+d}{2}}}$

${\displaystyle s-b={\frac {a-b+c+d}{2}}}$

${\displaystyle s-c={\frac {a+b-c+d}{2}}}$

${\displaystyle s-d={\frac {a+b+c-d}{2}}}$

இவ்வாய்ப்பாடு முக்கோணத்தின் பரப்பு காணும் ஹீரோனின் வாய்ப்பாட்டின் பொதுமைப்படுத்தப்பட்டப் படிவமாக அமைகிறது. பிரம்மகுப்தரின் வாய்ப்பாட்டில் d -ன் மதிப்பு பூச்சியத்தை நெருங்குவதாக எடுத்துக் கொண்டால் ஹீரோனின் வாய்ப்பாடு கிடைக்கும். அதாவது ஒரு பக்கத்தின் நீளம் பூச்சியமாக உள்ள நாற்கரமாக முக்கோணத்தைக் கொள்ளலாம்.

நிறுவல்

இப்பகுதியின் நிறுவலுக்குப் பயன்படுத்தப்படும் வட்ட நாற்கரத்தின் படம்.

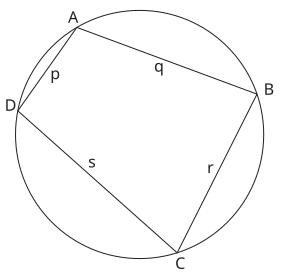
இப்பகுதியில் உள்ள படத்தில் தரப்பட்டுள்ள வட்ட நாற்கரத்தின் அளவுகளுக்கான குறியீடுகள் பரப்பு காணும்போது பயன்படுத்தப்படுகின்றன.

வட்ட நாற்கரம் ABCD -ன் பரப்பு

${\displaystyle =\triangle ADB}$ -ன் பரப்பு+ ${\displaystyle \triangle BDC}$ -ன் பரப்பு

${\displaystyle ={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin C.}$

${\displaystyle ABCD}$, ஒரு வட்ட நாற்கரம் என்பதால்:

${\displaystyle \angle DAB=180^{\circ }-\angle DCB.}$

${\displaystyle \sin A=\sin C\,}$

ஃ ${\displaystyle {\mbox{Area}}={\frac {1}{2}}pq\sin A+{\frac {1}{2}}rs\sin A}$

${\displaystyle ({\mbox{Area}})={\frac {1}{2}}\sin A(pq+rs)}$

${\displaystyle ({\mbox{Area}})^{2}={\frac {1}{4}}\sin ^{2}A(pq+rs)^{2}}$

${\displaystyle 4({\mbox{Area}})^{2}=(1-\cos ^{2}A)(pq+rs)^{2}=(pq+rs)^{2}-\cos ^{2}A(pq+rs)^{2}.\,}$

${\displaystyle \triangle }$ADB மற்றும் ${\displaystyle \triangle }$BDC, இரண்டின் பொதுப்பக்கம் DB-ன் மதிப்பைக் கொசைன் விதி மூலம் காண:

${\displaystyle DB=p^{2}+q^{2}-2pq\cos A=r^{2}+s^{2}-2rs\cos C.\,}$

${\displaystyle \cos C=\cos(\pi -A)=-\cos A\,}$ (${\displaystyle A}$, ${\displaystyle C}$ மிகைநிரப்புக் கோணங்கள்.)

இதனைப் பயன்படுத்த:

${\displaystyle p^{2}+q^{2}-2pq\cos A=r^{2}+s^{2}+2rs\cos A.\,}$

உறுப்புகளை மாற்றித் தொகுக்க:

${\displaystyle 2\cos A(pq+rs)=p^{2}+q^{2}-r^{2}-s^{2}.\,}$

${\displaystyle \cos A(pq+rs)={\frac {p^{2}+q^{2}-r^{2}-s^{2}}{2}}.\,}$

வர்க்கப்படுத்த:

${\displaystyle \cos ^{2}A(pq+rs)^{2}={\frac {(p^{2}+q^{2}-r^{2}-s^{2})^{2}}{4}}.\,}$

இதனைப் பரப்பு வாய்ப்பாட்டில் பிரதியிட:

${\displaystyle 4({\mbox{Area}})^{2}=(pq+rs)^{2}-{\frac {1}{4}}(p^{2}+q^{2}-r^{2}-s^{2})^{2}}$

${\displaystyle 16({\mbox{Area}})^{2}=4(pq+rs)^{2}-(p^{2}+q^{2}-r^{2}-s^{2})^{2},\,}$

${\displaystyle =(2(pq+rs)-p^{2}-q^{2}+r^{2}+s^{2})(2(pq+rs)+p^{2}+q^{2}-r^{2}-s^{2})\,}$

${\displaystyle =((r+s)^{2}-(p-q)^{2})((p+q)^{2}-(r-s)^{2})\,}$

${\displaystyle =(q+r+s-p)(p+r+s-q)(p+q+s-r)(p+q+r-s).\,}$

${\displaystyle S={\frac {p+q+r+s}{2}},}$ என எடுத்துக் கொண்டால்

${\displaystyle 16({\mbox{Area}})^{2}=16(S-p)(S-q)(S-r)(S-s).\,}$

${\displaystyle ({\mbox{Area}})^{2}=(S-p)(S-q)(S-r)(S-s).\,}$

வர்க்கமூலம் காண:

${\displaystyle {\mbox{Area}}={\sqrt {(S-p)(S-q)(S-r)(S-s)}}.}$

மாற்றுப் படிவம்

இவ்வாய்ப்பாட்டின் மற்றொரு படிவம்:

${\displaystyle K={\frac {\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}+8abcd-2(a^{4}+b^{4}+c^{4}+d^{4})}}{4}}\cdot }$

நிறுவல்

பரப்பு காணும் வாய்பாடின் பொதுப் படிவம்:

${\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}$

${\displaystyle s-a={\frac {-a+b+c+d}{2}}}$

${\displaystyle s-b={\frac {a-b+c+d}{2}}}$

${\displaystyle s-c={\frac {a+b-c+d}{2}}}$

${\displaystyle s-d={\frac {a+b+c-d}{2}}}$ இம்மதிப்புகளைப் பரப்பு வாய்பாடில் பிரதியிட:

${\displaystyle K={\sqrt {({\frac {-a+b+c+d}{2}})({\frac {a-b+c+d}{2}})({\frac {a+b-c+d}{2}})({\frac {a+b+c-d}{2}})}}}$

${\displaystyle ={\frac {1}{4}}{\sqrt {(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}}}$

${\displaystyle ={\frac {1}{4}}{\sqrt {[(c+d)-(a-b)][(c+d)+(a-b)][(a+b)-(c-d)][(a+b)+(c-d)]}}}$

${\displaystyle ={\frac {1}{4}}{\sqrt {[(c+d)^{2}-(a-b)^{2}][(a+b)^{2}-(c-d)^{2}]}}}$

${\displaystyle ={\frac {1}{4}}{\sqrt {[(c^{2}+d^{2}-a^{2}-b^{2}+2ab+2cd][(a^{2}+b^{2}-c^{2}-d^{2}+2ab+2cd]}}}$

${\displaystyle ={\frac {1}{4}}{\sqrt {[(2ab+2cd)-(a^{2}+b^{2}-c^{2}-d^{2})][(2ab+2cd)+(a^{2}+b^{2}-c^{2}-d^{2})]}}}$

${\displaystyle ={\frac {1}{4}}{\sqrt {(2ab+2cd)^{2}-(a^{2}+b^{2}-c^{2}-d^{2})^{2}}}}$

${\displaystyle ={\frac {1}{4}}{\sqrt {[(4a^{2}b^{2}+4c^{2}d^{2}+8abcd)-(a^{4}+b^{4}+c^{4}+d^{4}+2a^{2}b^{2}-2a^{2}c^{2}-2a^{2}d^{2}-2b^{2}c^{2}-2b^{2}d^{2}+2c^{2}d^{2})}}}$

${\displaystyle ={\frac {1}{4}}{\sqrt {(2a^{2}b^{2}+2a^{2}c^{2}+2a^{2}d^{2}+2b^{2}c^{2}+2b^{2}d^{2}+2c^{2}d^{2})+8abcd-(a^{4}+b^{4}+c^{4}+d^{4})}}}$

${\displaystyle ={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}-(a^{4}+b^{4}+c^{4}+d^{4})+8abcd-(a^{4}+b^{4}+c^{4}+d^{4})}}}$

${\displaystyle ={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2}+d^{2})^{2}+8abcd-2(a^{4}+b^{4}+c^{4}+d^{4})}}}$

வட்டத்துக்குள் அமையாத நாற்கரங்களுக்கு நீட்டிப்பு

வட்டத்துக்குள் அமையாத நாற்கரங்களின் பரப்பு காண்பதற்கு பிரம்மகுப்தரின் வாய்ப்பாட்டை நீட்டித்துக் கொள்ளலாம். இதற்கு நாற்கரங்களின் எதிர்க் கோணங்களின் அளவுகளைக் கருத்தில் கொள்ளல் வேண்டும்.

${\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd\cos ^{2}\theta }}}$ இது பிரெட்ஷ்னீடரின் வாய்ப்பாடாகும்.

இங்கு θ, நாற்கரத்தின் ஏதேனும் ஒரு சோடி எதிர்க் கோணங்களின் கூட்டுத்தொகையில் பாதி. இரண்டு சோடி எதிர்க் கோணங்களில் எந்த சோடியை வேண்டுமானாலும் எடுத்துக் கொள்ளலாம். ஏனெனில் மற்றொரு சோடி எதிர்க்கோணங்களின் கூட்டுத்தொகையில் பாதியானது, (180- θ) -ஆக இருக்கும். cos(180° − θ) = −cosθ, cos²(180° − θ) = cos²θ.

தரப்பட்ட பக்க நீளங்களைக் கொண்ட நாற்கரங்களிலேயே வட்ட நாற்கரங்கள் தான் மீப்பெரு பரப்புடையவை.

பொது நாற்கரங்களின் பரப்பு வாய்ப்பாட்டிலிருந்து வட்ட நாற்கரங்களின் பரப்பு காணும் வாய்ப்பாட்டைப் பெறுதல்:

வட்ட நாற்கரங்களின் பண்பின்படி அதன் எதிர்க் கோணங்கள் மிகைநிரப்புக் கோணங்கள். எனவே அவற்றின் கூடுதல் 180°, இக்கூடுதலின் பாதியளவு 90°

ஃ ${\displaystyle abcd\cos ^{2}\theta =abcd\cos ^{2}\left(90^{\circ }\right)=abcd\cdot 0=0,\,}$

எனவே பரப்பு வாய்ப்பாட்டில் இதைப் பிரதியிட வட்ட நாற்கரத்தின் பரப்பு காணும் பிரம்மகுப்தரின் வாய்ப்பாடு கிடைக்கிறது:

${\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)}}}$

ஜூலியன் கூலிட்ஜ் -ஆல் நிறுவப்பட்ட பொதுக் குவிவு நாற்கரங்களின் பரப்பு காணும் வாய்ப்பாடு:^[1]

${\displaystyle K={\sqrt {(s-a)(s-b)(s-c)(s-d)-\textstyle {1 \over 4}(ac+bd+pq)(ac+bd-pq)}}\,}$

இங்கு p மற்றும் q -நாற்கரத்தின் மூலைவிட்டங்களின் நீளங்கள்.

டாலமியின் தேற்றப்படி, ஒரு வட்ட நாற்கரத்திற்கு, ${\displaystyle pq=ac+bd}$ -ஆக இருக்கும். இம்மதிப்பைப் பிரதியிட கூலிட்ஜின் வாய்ப்பாடு, பிரம்மகுப்தரின் வாய்ப்பாடாக மாறும்.

தொடர்புள்ள பிற தேற்றங்கள்

• முக்கோணங்களின் பரப்பு காணும் ஹீரோனின் வாய்ப்பாடு - நாற்கரத்தின் பக்க நீளம் d = 0 எனக் கொள்வதால் கிடைக்கும் சிறப்பு வகை.
• பிரம்மகுப்தரின் பொது வாய்ப்பாட்டிற்கும் நீட்டிக்கப்பட்ட வாய்ப்பாட்டிற்கும் உள்ள தொடர்பு, கொசைன் விதியானது பித்தகோரஸ் தேற்றத்தின் நீட்டிப்பாக அமைதலுக்குச் சமமானது.

வெளி இணைப்புகள்

• MathWorld: Brahmagupta's formula