வடிவவியல் உருமாற்றம்

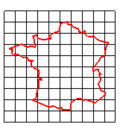
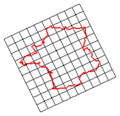
வடிவவியல் உருமாற்றம் (geometric transformation) என்பது சில வடிவவியல் அமைப்புகளைக் கொண்ட கணத்திலிருந்து அதே கணத்தை அல்லது அதைப்போன்ற வேறொரு கணத்தைத் தொடர்புபடுத்தும் ஒரு இருவழிக்கோப்பு ஆகும். குறிப்பாக, "வடிவவியல் உருமாற்றம் என்பது புள்ளிகளின் கணங்களை ஆட்களமாகவும் வீச்சாகவும் கொண்ட சார்பாகும். பெரும்பாலும் ஒரு வடிவவியல் உருமாற்றத்தின் ஆட்களம், வீச்சு இரண்டுமே R² அல்லது R³ ஆக இருக்கும். பெரும்பான்மை வடிவவியல் உருமாற்றங்கள் 1-1 சார்புகளாக இருப்பதால் அவற்றுக்கு நேர்மாறு உண்டு." ^[1] இந்த உருமாற்றங்களைப் பற்றி அறிந்துகொள்வதன் மூலமாக வடிவவியலைத் தெரிந்து கொள்ளலாம்.^[2]

வடிவவியல் உருமாற்றங்களின் ஆட்களங்களின் பரிமாணங்களைக் கொண்டு அவற்றை வகைப்படுத்தலாம். அதாவது அவை தள உருமாற்றங்களா அல்லது வெளி உருமாற்றங்களா எனக் காணலாம். மேலும், அவை பாதுகாக்கும் பண்புகளைக் கொண்டும் அவற்றை வகைப்படுத்தலாம்:

• இடப்பெயர்ச்சிகள் தூரங்களையும் திசைப்போக்குடைய கோணங்களையும் பாதுகாக்கின்றன.
• சமஅளவை உருமாற்றங்கள் தூரங்களையும் கோணங்களையும் பாதுகாக்கின்றன.^[3]
• வடிவொப்புமைகள் தூரங்களுக்கு இடைப்பட்ட விகிதங்களைப் பாதுகாக்கின்றன.
• கேண்முறை உருமாற்றங்கள் இணைத்தன்மையைப் பாதுகாக்கின்றன^[3]
• வீழ்ப்பு உருமாற்றங்கள் ஒருகோட்டுத்தன்மையைப் பாதுகாக்கின்றன.^[4]

இவை ஒவ்வொன்றும் முந்தைய வகை உருமாற்றத்தை உள்ளடக்கியவையாகும்.^[4]

• நேர்மாற்றல் தளங்களில் அமையும் கோடுகள், வட்டங்களைப் பாதுகாக்கின்றன; மோபியஸ் உருமாற்றங்கள் முப்பரிமாணத்தில் தளங்களையும் கோளங்களையும் பாதுகாக்கின்றன.

• 
  மூல உரு
• 
  சம அளவை உருமாற்றம்
• 
  வடிவொப்புமை
• 
  கேண்முறை உருமாற்றம்
• 
  வீழ்ப்பு உருமாற்றம்
• 
  நேர்மாற்றல்

ஒரேவகையைச் சேர்ந்த உருமாற்றங்கள் அனைத்தும் சார்புகளின் தொகுப்பு செயலைப் பொறுத்து ஒரு குலம் ஆகும். இவை பிற உருமாற்றங்களின் உட்குலங்களாகவும் அமையலாம்.