வட்டவிலகல்

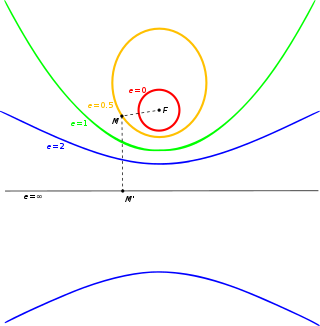
கணிதத்தில் வட்டவிலகல் (Eccentricity) என்பது அனைத்து கூம்பு வடிவத்திற்கும் அறியப்படும் ஒரு கணிதவியல் கருத்தாகும். இஃதை அவ்வடிவம் வட்ட வடிவிலிருந்து எந்தளவிற்கு பிறழ்ந்துள்ளது என்பதன் அளவாய் கொள்ளலாம். குறிப்பாக,

• ஒரு வட்டத்தின் வட்டவிலகல் சுழி அல்லது பூஜ்யம்
• ஒரு நீள்வட்டத்தின் வட்டவிலகல் சுழியைவிட அதிகம் ஆனால் 1-க்கும் குறைவு
• ஒரு பரவளைவின் வட்டவிலகல் 1
• ஒரு அதிபரவளைவின் வட்டவிலகல் 1-க்கு மேல், ஆனால் முடிவிலிக்கு குறைவு
• ஒரு நேர்கோட்டின் வட்டவிலகல் அது வருனிக்கப்பட்ட வகையை வைத்து 1-ஆகவோ அல்லது முடிவிலியாகவோ இருக்கும்

எல்லா வகையான கூம்பு வடிவங்களும், அவற்றின் வட்டவிலகல்கள் ஏறுமுகமாய் தரப்பட்டுள்ளன. வட்டவிலகலோடு வளைவுத்தன்மை குறைவதையும், இவ்வடிவங்கள் ஒன்றோடொன்று வெட்டாதிருப்பதையும் காண்க.

வட்டவிலகலின் வரையறை பின்வருமாறு தரப்படும்:

${\displaystyle e={\sqrt {1-k{\frac {b^{2}}{a^{2}}}}};\,\!}$

இதில், ${\displaystyle a\,\!}$ என்பது அவ்வடிவத்தின் அரை-பெரும் அச்சின் நீளம், ${\displaystyle b\,\!}$ என்பது அரை-சிறு அச்சின் நீளம் மற்றும் k என்பது நீள்வட்டதிற்கு +1, பரவளைவிற்கு 0, அதிபரவளைவிற்கு -1 எனவாகும்.

இஃது முதல் வட்டவிலகல்' எனவும் அறியப்படும், கணித இலகுவிற்காக கொள்ளப்படும் இரண்டாம் வட்டவிலகலினிருந்து e பிரித்தறிய இவ்வாறு குறிக்கப்படும். இரண்டாம் வட்டவிலகல் பின்வருமாறு வருனிக்கப்படும்:

${\displaystyle e'={\sqrt {k{\frac {a^{2}}{b^{2}}}-1}};\,\!}$

மேலும், இவையிரண்டும் கீழ்கண்டவாறு தொடர்புடையன:

${\displaystyle 1=(1-e^{2})(1+e'^{2});\,\!}$

நீள்வட்டம்

குவியங்கள், அச்சுகள் மற்றும் நேரியல் வட்டவிலகல் காட்டப்பெற்ற நீள்வட்டம்

அரை-பெரும் அச்சின் நீளம் ${\displaystyle a\,\!}$ எனவும், அரை-சிறு அச்சின் நீளம் ${\displaystyle b\,\!}$ எனவுமுடைய எந்தவொரு நீள்வட்டதிற்கும் அதன் வட்டவிலகல், e, என்பது அவ்வடிவின் கோணவட்ட விலகலின், ${\displaystyle o\!\varepsilon \,\!}$, சைனாகும் என்பது கீழ்கண்ட சமன்பாட்டின்படி அறியப்படும்:

 ${\displaystyle o\!\varepsilon =\arccos \left({\frac {b}{a}}\right)=2\arctan \left({\sqrt {\frac {a-b}{a+b}}}\right);\,\!}$

வட்டவிலகல் என்பது குவியங்களுக்கு (${\displaystyle F_{1}\,\!}$ மற்றும் ${\displaystyle F_{2}\,\!}$) இடையிலான தொலைவு மற்றும் பெரும் அச்சின் நீளத்திற்கான விகிதமாகும் ${\displaystyle {}_{\left({\frac {\overline {F_{1}F_{2}}}{\overline {AB}}}\right)}\,\!}$.

அதேபோல், இரண்டாம் வட்டவிலகல், e', ${\displaystyle o\!\varepsilon \,\!}$ன் டேன் ஆகும்:

${\displaystyle e'=\tan(o\!\varepsilon )={\sqrt {{\frac {a^{2}}{b^{2}}}-1}};\,\!}$

நேர்கோடு

ஒரு நேர்கோட்டை அல்லது கோட்டுத்துண்டை சிறு அச்சின் நீளம் சுழி (பூஜ்யம்) எனக்கொண்ட ஒரு நீள்வட்டம் என்பதாக கொள்ளலாம், அதன்படி ${\displaystyle b\,\!}$ சுழியாகும். ${\displaystyle b\,\!}$-ன் இந்த மதிப்பை நீள்வட்டத்தின் வட்டவிலகல் காணும் சமன்பாட்டில் ஏற்ற, அதன் வட்டவிலகல் 1 எனப்பெறலாம்.

கூம்பு வெட்டின் மாற்று வரையருவாக, அஃது புள்ளி P மற்றும் வரைகோடு L-ஐ சுற்றி புள்ளிகள் Q-வின் ஒழுக்கு எனக்கொள்கையில், ${\displaystyle {\overline {PQ}}=e{\overline {LQ}}}$ என்பதாகவும், ${\displaystyle {\overline {LQ}}}$ என்பது Q-விற்கும் L-க்குமான செங்குத்து தொலைவாகவும், e என்பது வட்டவிலகல் என்றுமாகையில், e = ∞ மதிப்பு ஒரு நேர்கோட்டை ஈனும் (தரும்).

அதிபரவளைவு

அரை-பெரும் அச்சின் நீளம் ${\displaystyle a\,\!}$ எனவும், அரை-சிறு அச்சின் நீளம் ${\displaystyle b\,\!}$ எனவுமுடைய எந்தவொரு அதிபரவளைவிற்கும் அதன் வட்டவிலகல் கீழ்கண்ட சமன்பாட்டின்படி அறியப்படும்:

${\displaystyle e={\sqrt {1+{\frac {b^{2}}{a^{2}}}}};\,\!}$

பரப்புகள்

ஒரு பரப்பின் வட்டவிலகல் என்பது அப்பரப்பின் குறிப்பிட்ட ஒரு பகுதியின் (அல்லது வெட்டின்) வட்டவிலகலாகும். எடுத்துக்காட்டாய், ஒரு மூவச்சு நீள்கோளத்தின் உச்சி வட்டவிலகல் என்பது மிகப்பெரிய மற்றும் மிகச்சிறிய அச்சுக்களை (இவற்றில் ஒன்று முனையிடை (துருவ) அச்சாக இருக்கும்) உள்ளடக்கிய தளவெட்டுப்பகுதியில் தோன்றும் நீள்வட்டதின் வட்டவிலகலாகும், மற்றும், நடுவரை வட்டவிலகல் என்பது முனையிடை (துருவ) அச்சிற்கு செங்குத்தாய் மையத்தில் இருக்கும் தளவெட்டில் (அஃதாவது, நடுவரைத் தளத்தில்) காணப்படும் நீள்வட்டதின் வட்டவிலகலாகும்.

வானியக்கவியல்

வானியக்கவியலில், கோளவடிவ புலனிலையால் கட்டுற்ற சுற்றுப்பாதைகளுக்கு மேற்கூறிய வரையறை முறையின்றி நுண்பியலாக்கப்படுகிறது. மிகைமையத் தொலைவும் குறைமையத் தொலைவும் நிகராய் இருக்கையில் வட்டவிலகல் குறைவு எனவும், அவையிரண்டும் மிகவேறுபட்டு இருக்கையில் அச்சுற்றுப்பாதை வட்டத்தினின்று மிகுதியாக பிறழ்ந்துள்ளது, அதன் வட்டவிலகல் ஏறத்தாழ 1 எனவும் கொள்ளப்படுகிறது. இவ்வரையறை, கெப்லெரியன் புலனிலைகளில் (அஃதாவது, ${\displaystyle 1/r}$ புலனிலை), நீள்வட்டதிற்கான வட்டவிலகலின் கணித வரையறையுடன் ஒத்துப்போகின்றது.

இவற்றையும் பார்க்கவும்

• சுற்றுப்பாதையின் வட்டவிலகல்
• சுற்றுப்பாதையின் நிலைத் திசையன்