நீள்வட்டம்

கணிதத்தில் நீள்வட்டம் (பிரான்சியம், ஆங்கிலம், இடாய்ச்சு:ellipse, எசுப்பானியம், போர்த்துகீசியம்:elipse) என்பது ஒருவகையான கூம்பு வெட்டு ஆகும். கூம்பு வடிவொன்றை, தளம் ஒன்று வெட்டும்போது (அதன் அடியை வெட்டாமல்) கிடைக்கும் வெட்டுமுகம் நீள்வட்டம் ஆகும். நீள்வட்டத்தின் ஆங்கிலப் பெயரான ellipse என்பது ἔλλειψις -elleipsis என்ற கிரேக்கச் சொல்லிருந்து உருவானது.

ஓர் நேர்வட்டக்கூம்பை ஒரு தளத்தால் வெட்டக் கிடைக்கும் வெட்டுமுகமாகக் பெறப்படும் நீள்வட்டம்

சனிக்கோளின் வளையங்கள் வட்டமாக இருந்தாலும் ஒரு கோணத்தில் பார்க்கும்போது அவை படத்தில் உள்ளது போல நீள்வட்டமாகத் தோற்றமளிக்கிறன. நிழற்படம்:ESO

ஒரு கூம்பை அதன் அச்சுக்கு செங்குத்தான தளத்தில் வெட்டினால் கிடைக்கும் வெட்டுமுகம் ஒரு நீள்வட்டத்துக் மாறாக வட்டமாக இருக்கும். ஆனால் ஓர் உருளையை அதன் முக்கிய சமச்சீர் அச்சுக்கு இணையாக இல்லாத ஒரு தளத்தால் வெட்டும்போதும் ஒரு நீள்வட்டம் கிடைக்கும்.

வட்டத்துக்கு நடு இருப்பது போலவும் எப்படி நடுவில் இருந்து வட்டத்தின் ஒவ்வொரு புள்ளியும் ஒரே தொலைவில் இருக்குமோ அப்படி நீவட்டத்துக்கு இரண்டு நிலையான புள்ளிகள் உண்டு. அந்த இரண்டு புள்ளிகளில் இருந்து நீவட்டத்தின் ஒவ்வொரு புள்ளியும் ஒரே கூட்டுத்தொகை அளவில் திலைவு இருக்கும். இது நீவட்டத்தின் ஒரு [மாறிலி]]யாக இருக்கும். இந்த இரண்டு நிலையான புள்ளிகளும் நீள்வட்டத்தின் குவியங்கள் எனப்படுகின்றன.

இரண்டு ஊசிகளையும், ஒரு நூல் தடத்தையும், பென்சில் ஒன்றையும் பயன்படுத்தி ஒரு நீள்வட்டத்தை வரைய முடியும்.

நீள்வட்டத்தின் கூறுகள்

நீள்வட்டமும் அதன் சில கணிதப்பண்புகளும்.

அச்சுகள்

நீள்வட்டமானது அதன் கிடைமட்ட மற்றும் நிலைக்குத்தான இரு அச்சுகளைப் பொறுத்து சமச்சீராக அமையும் ஒரு மூடிய வளைவரை. கிடைமட்ட அச்சு நீள்வட்டத்தின் நெட்டச்சு (முக்கிய அச்சு; நீளம் 2a) எனவும், நிலைக்குத்து அச்சு நீள்வட்டத்தின் சிற்றச்சு (துணை அச்சு; நீளம் 2b) எனவும் அழைக்கப்படுகின்றன.

நெட்டச்சும் குற்றச்சும் சந்திக்கும் புள்ளி நீள்வட்டத்தின் மையம்.

நீள்வட்டத்தின் மையத்தை நடுப்புள்ளியாகக் கொண்டு நீள்வட்டத்தின் மீது அமையும் இரு புள்ளிகளுக்கு இடையேயுள்ள தூரம், அவை நெட்டச்சின் முனைகளாக இருக்கும்போது மிக அதிகமானதாகவும், சிற்றச்சின் முனைகளாக இருக்கும்போது மிகச் சிறியதாகவும் இருக்கும்.^[1]

நெட்டச்சில் பாதி அரை நெட்டச்சு (a) எனவும் சிற்றச்சில் பாதி அரைச் சிற்றச்சு (b) எனவும் அழைக்கப்படும்.^{[2][3][4][5][6][7][8][9]}

குவியங்கள்

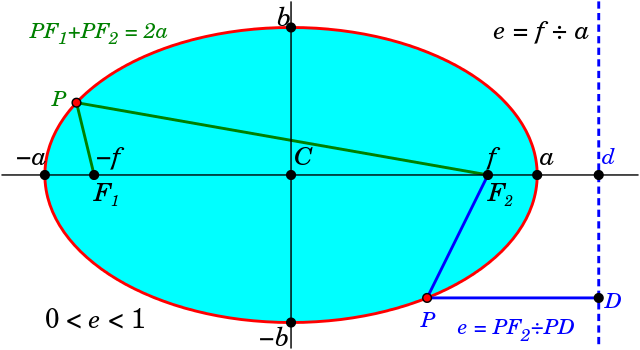
நீள்வட்டத்துக்கு இரு குவியங்கள் உள்ளன. இவை நீள்வட்டத்தின் மையத்திலிருந்து சமதூரத்தில் உள்ளவாறு நெட்டச்சின் மீது அமைந்த இரு புள்ளிகளாகும். இவை F₁ மற்றும் F₂ எனக் குறிக்கப்படுகின்றன. நீள்வட்டத்தின் மீதமையும் ஏதேனும் ஒரு புள்ளிக்கும் இவ்விரு குவியங்களுக்கும் இடைப்பட்ட தூரங்களின் கூடுதல் மாறிலியாகவும் அம்மாறிலி நெட்டச்சின் நீளத்திற்குச் சமமானதாகவும் இருக்கும்.

${\displaystyle PF_{1}+PF_{2}=2a}$.

வட்ட விலகல்

நீள்வட்டத்தின் வட்டவிலகல் ε அல்லது e எனக் குறிக்கப்படுகிறது. இதன் மதிப்பு நீள்வட்டத்தின் குவியங்களுக்கு இடையேயுள்ள தூரம் (2f) மற்றும் நெட்டச்சின் நீளம் (2a) இரண்டிற்குமான விகிதமாகும்.

${\displaystyle e={\frac {2f}{2a}}={\frac {f}{a}}}$

நீள்வட்டத்தின் வட்டவிலகலின் எண்மதிப்பு 0 மற்றும் 1 -க்கு இடைப்பட்டது. (0<e<1).

• e =0 எனில் குவியம் நீள்வட்டத்தின் மையத்துடன் ஒன்றும். அதனால் நீள்வட்டம் வட்டமாகி விடும்.

• e இன் மதிப்பை 1 ஐ நெருங்கும்போது:

• • இரு குவியங்களுக்கு இடையேயுள்ள தூரம் முடிவுறு மதிப்பாக இருந்தால் நீள்வட்டம் ஒரு கோட்டுத்துண்டாக தோன்ற ஆரம்பிக்கும்.
  • ஒரு குவியம் நிலையான இடத்திலும் மற்றொரு குவியம் முடிவிலியை நோக்கித் தூரமாக நகர்ந்தால் பரவளையமாகவும் தோன்றும்.^[10]

${\displaystyle f=ae}$ என்பது நீள்வட்டத்தின் ஒரு குவியத்திற்கும் மையத்திற்கும் இடைப்பட்ட தூரம். இது நேரியல் வட்ட விலகல் எனப்படும்.

செவ்வகலம்

நீள்வட்டத்தின் குவியங்களின் வழியாக அதன் இயக்குவரைகளுக்கு இணையாக வரையப்பட்ட நாண் நீள்வட்டத்தின் செவ்வகலம் (latus rectum) எனப்படும். செவ்வகலத்தில் பாதி அரைச் செவ்வகலம் எனப்படும். செவ்வகலத்தின் நீளம்: ${\displaystyle {\frac {2b^{2}}{a}}}$

நீள்வட்டம் வரைதல்

ஊசிகள் - வரைகோல் முறை

வரைகோல், இரு ஊசிகள் மற்றும் நூல் கொண்டு நீள்வட்டம் வரைதல்

இரு நிலையான புள்ளிகளிலிருந்து உள்ள தூரங்களின் கூடுதல் எப்பொழுதும் சமமாகவே உள்ளவாறு இயங்கும் புள்ளியின் இயங்குவரை நீள்வட்டம் என்ற வரையறையைக் கொண்டு இம்முறையில் நீள்வட்டம் வரையப்படுகிறது^[11]:

தேவையான பொருட்கள்:

வரைதாள், வரைகோல், இரு ஊசிகள் மற்றும் நூல்.

வரைமுறை:

வரைதாளில் ஒரு குறிப்பிட தூரத்தில் உள்ளபடி இரு ஊசிகளும் குத்தி வைக்கப்படுகின்றன. நூலின் இரு முனைகளும் இந்த ஊசிகளில் கட்டப்படுகின்றன. பின்னர் வரைகோல் இரு ஊசிகளுக்கு இடையில் ஒரு முக்கோண வடிவாக உள்ளவாறு நூலோடு கட்டப்படுகிறது. இப்பொழுது நூலைத் தொய்வில்லாமல் பிடித்துக் கொண்டு வரைகோலை நகர்த்தி வரையத் தொடங்க வேண்டும். தொடங்கிய இடத்தை மீண்டும் வந்தடையும் போது ஒரு நீள்வட்டம் முழுமையாக வரையப்பட்டிருக்கும். இம்முறை நீள்வட்ட வடிவில் மலர்ப்படுகை அமைப்பதற்கு பயன்பட்டதால் தோட்டக்காரரின் நீள்வட்டம் என அழைக்கப்படுகிறது.^[12]

பிற முறைகள்

ஆர்க்கிமிடீசின் வளைக்கவராயம் -அசைப்படம்

ஒரு அளவுகோல், மூலைமட்டம் மற்றும் வரைகோல் கொண்டு ஒரு நீள்வட்டம் வரையலாம்:

ஒரு வரைதாளில் M,N என்ற ஒன்றுக்கொன்று செங்குத்தான இரு கோடுகளை வரைக. இவையிரண்டும் நீள்வட்டத்தின் நெட்டச்சு மற்றும் சிற்றச்சாக அமையும். A->C நெட்டச்சின் நீளமாகவும் B->C சிற்றச்சின் நீளமாகவும் உள்ளவாறு அளவுகோலின் மேல் A, B, C என மூன்று புள்ளிகளைக் குறித்துக் கொள்ள வேண்டும். எப்பொழுதுமே புள்ளி A கோடு N இல் உள்ளபடியும், புள்ளி B கோடு M இல் உள்ளபடியும் அளவுகோலை ஒரு கையால் திருப்பி நகர்த்திக் கொண்டே போக வேண்டும். மற்றொரு கையால் வரைகோலின் முனை, புள்ளி C இன் பாதையை வரையட்டும். இதனால் கிடைக்கும் வரைபடம் ஒரு நீள்வட்டமாக இருக்கும்.

ஆர்க்கிமிடீசின் வளைக்கவராயம் அல்லது நீள்வட்ட வரைவி (ellipsograph) என்பது மேலே பயன்படுத்தப்பட்ட முறையில் அமைக்கப்பட்ட ஒரு கருவி. இக்கருவி அளவுகோலுக்குப் பதில் ஒரு முனையில் வரைகோலைப் (C) பிடித்துக் கொள்ளக்கூடிய ஒரு அமைப்பும், ஒரு உலோகத் தகட்டில் அமைந்த இரு செங்குத்தான காடிகளில் நகரக்கூடிய மாற்றியமைக்கக் கூடிய இரு ஊசிகளையும் (A, B) உடைய ஒரு தடியைக் கொண்டிருக்கும்.^[13]

கணித வரையறைகளும் பண்புகளும்

யூக்ளிடிய வடிவவியலில்

வரையறை

• யூக்ளிடிய வடிவவியலில் வழக்கமாக நீள்வட்டமானது கூம்பு வெட்டின் வெட்டுப்பகுதியாகவோ அல்லது இரு நிலையான புள்ளிகளிலிருந்து (குவியங்கள்) உள்ள தூரங்களின் கூடுதல் எப்பொழுதும் சமமாகவே உள்ள புள்ளிகளால் அமைந்த வடிவமாகவோ வரையறுக்கப்படுகிறது.

• தளத்தில் ஒரு தரப்பட்ட புள்ளியிலிருந்து (குவியம்) உள்ள தூரம் மற்றும் தரப்பட்டக் கோட்டிலிருந்து (இயக்குவரை) அமையும் தூரம் இவை இரண்டின் விகிதம் எப்பொழுதும் மாறிலியாகவும் அம்மாறிலியின் மதிப்பு 1 -ஐ விடக் குறைவாகவும் உள்ளவாறு அமைகின்ற புள்ளிகளால் ஆனதாகவும் ஒரு நீள்வட்டத்தை வரையறுக்கலாம்.

• தரப்பட்ட ஒரு புள்ளியிலிருந்தும் (குவியம்) ஒரு குறிப்பிட்ட வட்டத்திலிருந்தும் (இயக்கு வட்டம்) சமதூரத்தில் அமையும் புள்ளிகளால் அமைந்த வளைவரையாகவும் நீள்வட்டத்தை வரையறுக்கலாம்.

சமன்பாடுகள்

கார்ட்டிசியன் ஆய அச்சுக்களோடு ஒன்றும் நெட்டச்சு, சிற்றச்சுக்களைக் கொண்ட நீள்வட்டத்தின் சமன்பாடு: ${\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.}$

குவியம்

நீள்வட்டத்தின் மையம் C -க்கும் ஏதேனும் ஒரு குவியத்துக்கும் இடைப்பட்ட தூரம்:

${\displaystyle f=ae}$,

${\displaystyle f={\sqrt {a^{2}-b^{2}}}.}$

வட்ட விலகல்

${\displaystyle e=\varepsilon ={\sqrt {\frac {a^{2}-b^{2}}{a^{2}}}}={\sqrt {1-\left({\frac {b}{a}}\right)^{2}}}=f/a}$

இயக்குவரை

நீள்வட்டத்தின் ஒவ்வொரு குவியம் F உடனும் சிற்றச்சுக்கு இணையான ஒரு கோடு தொடர்புபடுத்தப்படுகிறது. இக்கோடு நீள்வட்டத்தின் இயக்குவரை எனப்படும். நீள்வட்டத்தின் மேல் அமையும் எந்தவொரு புள்ளிக்கும் குவியம் F -க்கும் இடைப்பட்ட தூரம் மற்றும் அப்புள்ளியிலிருந்து இயக்குவரைக்கு உள்ள செங்குத்து தூரம் ஆகிய இரண்டின் விகிதம் மாறிலியாக இருக்கும். இம்மாறிலியானது, நீள்வட்டத்தின் வட்ட விலகல்:

${\displaystyle e={\frac {PF}{PD}}}$.

வட்ட இயக்குவரை

ஒரு குவியத்திலிருந்தும் மற்றொரு குவியத்தை மையமாகக் கொண்ட வட்டத்திலிருந்தும் சமதூரத்தில் உள்ள புள்ளிகளால் ஆன வளைவரையாக நீள்வட்டத்தை வரையறுக்கலாம். இதில் கூறப்படும் வட்டம் நீள்வட்டத்தின் இயக்கு வட்டம் எனப்படும். இவ்வட்டத்தின் ஆரம் வட்டத்தின் மையமான ஒரு குவியத்திற்கும் மற்றொரு குவியத்திற்கும் இடைப்பட்ட தூரத்தை விட அதிகமாக இருக்கும். இதனால் முழு நீள்வட்டமும் இரு குவியங்களும் இயக்கு வட்டத்துள்ளாக அமையும்.

ஒரு உட்சில்லுருவாக

 R = 2r எனும்போது உட்சில்லுருவின் சிறப்புவகையாக அமையும் நீள்வட்டம் (சிவப்பு).

 R = 2r எனில் ஒரு உட்சில்லுரு நீள்வட்டமாகும்.

நாண்கள்

நீள்வட்டத்தின் இணை நாண்களின் நடுப்புள்ளிகள் ஒரே கோட்டில் அமையும்.^[14]:p.147

பகுமுறை வடிவவியலில்

பொது நீள்வட்டம்

பகுமுறை வடிவவியலில் நீள்வட்டமானது,

${\displaystyle ~AX^{2}+BXY+CY^{2}+DX+EY+F=0}$

என்ற சமன்பாட்டை

${\displaystyle B^{2}-4AC<0,}$

கட்டுப்பாட்டுக்கு உட்பட்டு நிறைவு செய்யும் ${\displaystyle (X,Y)}$ புள்ளிகளாலான (கார்ட்டீசியன் தளம்) வளைவரையாக வரையறுக்கப்படுகிறது.^[15][16]

நியமன வடிவம்

பகுமுறை வடிவவியலில் நீள்வட்டச் சமன்பாட்டின் நியமன வடிவம்:

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1}$ ${\displaystyle a>b,}$

இந்நீள்வட்டத்தின்

• மையம்:(0,0)
• நெட்டச்சு -${\displaystyle x}$-அச்சு
• சிற்றச்சு -${\displaystyle y}$-அச்சு
• நெட்டச்சின் நீளம் =2a
• சிற்றச்சின் நீளம் =2b
• குவியங்கள்: ${\displaystyle (-ea,0)}$ மற்றும் ${\displaystyle (+ea,0)}$
• இயக்குவரைகளின் சமன்பாடுகள்: ${\displaystyle x=\pm {\frac {a}{e}}}$
• வட்டவிலகல்: ${\displaystyle e={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}}$
• செவ்வகலத்தின் நீளம் =${\displaystyle {\frac {2b^{2}}{a}}}$

மேற்கோள்கள்

• Besant, W.H. (1907). "Chapter III. The Ellipse". Conic Sections. London: George Bell and Sons. p. 50. {{cite book}}: Invalid |ref=harv (help)
• Miller, Charles D.; Lial, Margaret L.; Schneider, David I. (1990). Fundamentals of College Algebra (3rd ed.). Scott Foresman/Little. p. 381. ISBN 0-673-38638-4.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Mercier, Dany-Jack (2015). Fondamentaux de géométrie. Paris, France: CSIPP. p. 143. ISBN 978-1-517-23785-1.
• Coxeter, H.S.M. (1969). Introduction to Geometry (2nd ed.). New York: Wiley. pp. 115–9.
• Ellipse at Planetmath பரணிடப்பட்டது 2010-06-20 at the வந்தவழி இயந்திரம்
• Weisstein, Eric W., "Ellipse", MathWorld.