Гіперболічний рух (теорія відносності)

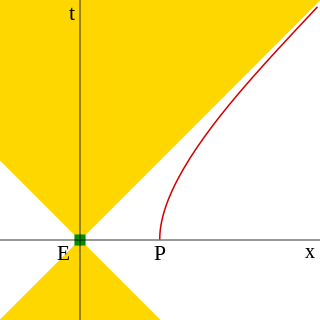
Гіперболічний рух — це рух об'єкта з постійним Власне прискорення в спеціальній теорії відносності. Його називають гіперболічним рухом, тому що рівняння, що описує траєкторію об'єкта в просторі-часі, є гіперболою, як це можна побачити, якщо побудувати графік на діаграмі Мінковського, координати якої представляють відповідну інерціальну (неприскорену) систему. Цей рух має кілька цікавих особливостей, зокрема, той факт, що фотон можна випередити, якщо мати достатню перевагу на старті, як це можна побачити на діаграми^[1].

Гіперболічний рух можна відобразити на діаграмі Мінковського, де рух прискорюваної частинки відбувається вздовж осі ${\displaystyle X}$. Кожна гіпербола визначається виразами ${\displaystyle x=\pm c^{2}/\alpha }$ і ${\displaystyle \eta =\alpha \tau /c}$ (де${\displaystyle c=1,\alpha =1}$) у рівнянні (2).

Історія

Герман Мінковський (1908) показав зв'язок між точкою на світовій лінії та величиною 4-прискорення та «гіперболи викривлення» (нім. Krümmungshyperbel)^[2]. У контексті жорсткості Борна^[en], Макс Борн (1909) згодом ввів термін «гіперболічний рух» (нім. Hyperbelbewegung) для випадку постійної величини 4-прискорення, і потім надав детальний опис заряджених частинок у гіперболічному русі та ввів відповідну «гіперболічно прискорену систему відліку» (нім. hyperbolisch beschleunigtes Bezugsystem)^[3]. Формули Борна були спрощені та розширені Арнольдом Зоммерфельдом (1910)^[4]. З першими оглядами можна ознайомитись у підручниках Макса фон Лауе (1911, 1921)^[5] або Вольфганга Паулі (1921)^[6]. Див. також Galeriu (2015)^[7] або Gourgoulhon (2013)^[8], і розділ «Історія статті» Прискорення (спеціальна теорія відносності)^[en].

Світова лінія

Власне прискорення ${\displaystyle \alpha }$ частинки визначається як прискорення, яке «відчуває» частинка, коли вона прискорюється від однієї інерціальної системи відліку до іншої. Якщо власне прискорення спрямоване паралельно лінії руху, воно пов'язане зі звичайним 3-прискоренням спеціальної теорії відносності^[en] ${\displaystyle a=du/dT}$ формулою

${\displaystyle \alpha =\gamma ^{3}a={\frac {1}{\left(1-u^{2}/c^{2}\right)^{3/2}}}{\frac {du}{dT}},}$

де ${\displaystyle u}$ — миттєва швидкість частинки, ${\displaystyle \gamma }$ — фактор Лоренца, ${\displaystyle c}$ — це швидкість світла, а ${\displaystyle T}$ — координатний час. Розв'язання рівняння руху дає шукані формули, які можна виразити через координатний час ${\displaystyle T}$ а також власний час ${\displaystyle \tau }$. Для спрощення всі початкові значення часу, місця та швидкості можна встановити рівними 0, таким чином^{[5][6][9][10][11]}:

${\displaystyle {\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {\alpha T}{\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}}\\&=c\tanh \left(\operatorname {arsinh} {\frac {\alpha T}{c}}\right)\\X(T)&={\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}-1\right)\\&={\frac {c^{2}}{\alpha }}\left(\cosh \left(\operatorname {arsinh} {\frac {\alpha T}{c}}\right)-1\right)\\c\tau (T)&={\frac {c^{2}}{\alpha }}\ln \left({\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}+{\frac {\alpha T}{c}}\right)\\&={\frac {c^{2}}{\alpha }}\operatorname {arsinh} {\frac {\alpha T}{c}}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh {\frac {\alpha \tau }{c}}\\\\X(\tau )&={\frac {c^{2}}{\alpha }}\left(\cosh {\frac {\alpha \tau }{c}}-1\right)\\\\cT(\tau )&={\frac {c^{2}}{\alpha }}\sinh {\frac {\alpha \tau }{c}}\\\\\\\end{aligned}}\end{array}}}$

(1)

Це призводить до рівняння ${\displaystyle \left(X+c^{2}/\alpha \right)^{2}-c^{2}T^{2}=c^{4}/\alpha ^{2}}$, що є гіперболою в часі T і змінною простору ${\displaystyle X}$. У цьому випадку прискорений об'єкт знаходиться на ${\displaystyle X=0}$ у момент часу ${\displaystyle T=0}$. Якщо натомість є початкові значення, відмінні від нуля, формули для гіперболічного руху приймають наступний вигляд^[12][13][14]:

${\displaystyle {\scriptstyle {\begin{array}{c|c}{\begin{aligned}u(T)&={\frac {u_{0}\gamma _{0}+\alpha T}{\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}}\quad \\&=c\tanh \left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right\}\\X(T)&=X_{0}+{\frac {c^{2}}{\alpha }}\left({\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}-\gamma _{0}\right)\\&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right]-\gamma _{0}\right\}\\c\tau (T)&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\ln \left({\frac {{\sqrt {c^{2}+\left(u_{0}\gamma _{0}+\alpha T\right){}^{2}}}+u_{0}\gamma _{0}+\alpha T}{\left(c+u_{0}\right)\gamma _{0}}}\right)\\&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)-\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)\right\}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh \left\{\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right\}\\\\X(\tau )&=X_{0}+{\frac {c^{2}}{\alpha }}\left\{\cosh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-\gamma _{0}\right\}\\\\cT(\tau )&=cT_{0}+{\frac {c^{2}}{\alpha }}\left\{\sinh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-{\frac {u_{0}\gamma _{0}}{c}}\right\}\end{aligned}}\end{array}}}}$

Стрімкість

Світову лінію для гіперболічного руху (яку відтепер будемо записувати як функцію власного часу) можна спростити кількома способами. Наприклад, вираз

${\displaystyle X={\frac {c^{2}}{\alpha }}\left(\cosh {\frac {\alpha \tau }{c}}-1\right)}$

може бути піддано просторовому зсуву на ${\displaystyle c^{2}/\alpha }$, таким чином отримуємо

${\displaystyle X={\frac {c^{2}}{\alpha }}\cosh {\frac {\alpha \tau }{c}}}$, ^[15]

у відповідності до чого спостерігач знаходиться в точці ${\displaystyle X=c^{2}/\alpha }$ в момент часу ${\displaystyle T=0}$. Крім того, задавши ${\displaystyle x=c^{2}/\alpha }$ і вводячи стрімкість ${\displaystyle \eta =\operatorname {artanh} {\frac {u}{c}}={\frac {\alpha \tau }{c}}}$,^[14] рівняння гіперболічного руху зводяться до^[4][16]

${\displaystyle cT=x\sinh \eta ,\quad X=x\cosh \eta }$

(2)

з гіперболою ${\displaystyle X^{2}-c^{2}T^{2}=x^{2}}$.

Заряджені частинки в гіперболічному русі

Борн (1909)^[3], Зоммерфельд (1910)^[4], фон Лауе (1911)^[5], Паулі (1921)^[6] також сформулювали рівняння для електромагнітного поля заряджених частинок у гіперболічному русі^[7]. Це рівння було розширено Германом Бонді і Томасом Голдом (1955)^[17], а також Фултоном і Рорліхом (1960)^[18][19]:

${\displaystyle {\begin{aligned}E_{\rho '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 'z'}{\xi ^{\prime 3}}}\\E_{z'}'=&{\frac {-\left(4e/\alpha ^{2}\right)1/\alpha ^{2}+t^{\prime 2}+\rho ^{\prime 2}-z^{\prime 2}}{\xi ^{\prime 3}}}\\E_{\varphi '}'=&H_{\varphi '}'=H_{z'}'=0\\H_{\varphi '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 't'}{\xi ^{\prime 3}}}\\\xi '=&{\sqrt {\left(1/\alpha ^{2}+t^{\prime 2}-\rho ^{\prime 2}-z^{\prime 2}\right)^{2}+\left(2\rho '/\alpha \right)^{2}}}\end{aligned}}}$

Це пов'язано з суперечливим^[20][21] дискусійним питанням про те, чи випромінюють заряди в безперервному гіперболічному русі чи ні, і чи узгоджується це з принципом еквівалентності — навіть якщо мова йде про ідеальну ситуацію, оскільки вічний гіперболічний рух неможливий. У той час як ранні автори, такі як Борн (1909) або Паулі (1921), стверджували, що випромінювання не виникає, пізніші автори, такі як Бонді і Голд^[17], а також Фултон і Рорліх^[18][19], показали, що випромінювання насправді виникає.

Власна система відліку

Шлях світла через E позначає видимий горизонт подій спостерігача P у гіперболічному русі.

Докладніше: Координати Риндлера та Власна система відліку (плоский простір-час)

У рівнянні (2) для гіперболічного руху вираз ${\displaystyle x}$ був константою, тоді як стрімкість ${\displaystyle \eta }$ була змінною. Однак, як зазначив Зоммерфельд^[16], ${\displaystyle x}$ можна визначити як змінну, а ${\displaystyle \eta }$ зробити константой. Це означає, що рівняння стають перетвореннями, що вказує на одночасну форму спокою прискореного тіла з гіперболічними координатами ${\displaystyle (x,y,z,\eta )}$ як це бачить спостерігач, що рухається

${\displaystyle cT=x\sinh \eta ,\quad X=x\cosh \eta ,\quad Y=y,\quad Z=z}$

За допомогою цього перетворення власний час стає часом гіперболічно прискореної системи. Ці координати, які зазвичай називають координатами Ріндлера (подібні варіанти називаються координатами Коттлера-Меллера або координатами Ласса^[en]), розглядаються як окремий випадок координат Фермі або Власних координат і часто використовуються у зв'язку з ефектом Унру. При розгляді цих координат виявляється, що спостерігачі в гіперболічному русі мають видимий горизонт подій, з-за меж якого до них не може дійти жоден сигнал.

Спеціальне конформне перетворення

Менш відомим методом визначення системи відліку в гіперболічному русі є використання спеціального конформного перетворення^[en], що складається з інверсії^[en], трансляції та іншої інверсії^[22]. Його зазвичай інтерпретують як калібрувальне перетворення в просторі Мінковського, хоча деякі автори альтернативно використовують його як перетворення прискорення (див. Каструп для критичного історичного огляду)^[23]. Має наступну форму

${\displaystyle X^{\mu }={\frac {x^{\mu }-a^{\mu }x^{2}}{1-2ax+a^{2}x^{2}}}}$

Використовуючи лише один просторовий вимір ${\displaystyle x^{\mu }=(t,x)}$, а також подальше спрощення шляхом встановлення ${\displaystyle x=0}$, і використовуючи прискорення ${\displaystyle a^{\mu }=(0,-\alpha /2)}$, отримуємо^[24]

${\displaystyle T={\frac {t}{1-{\frac {1}{4}}\alpha {}^{2}t^{2}}},\quad X={\frac {-\alpha t^{2}}{2\left(1-{\frac {1}{4}}\alpha {}^{2}t^{2}\right)}}}$

з гіперболою ${\displaystyle \left(X-1/\alpha \right)^{2}-T^{2}=1/\alpha ^{2}}$. Виявляється, що при ${\displaystyle t=\pm (x+2/\alpha )}$ час стає сингулярним, на що Фултон, Рорліх і Віттен^[24] зауважують, що потрібно триматися подалі від цієї межі, тоді як Каструп^[23] (який дуже критично ставиться до цієї інтерпретації прискорення) зауважує, що це один із дивних результатів цієї інтерпретації.