Двійковий логарифм

В математиці, двійковий логарифм (log₂n) — це степінь, до якого треба піднести число 2, щоб отримати значення n. Тобто, для будь-якого дійсного числа x, виконується еквівалентність

${\displaystyle x=\log _{2}n\quad \Longleftrightarrow \quad 2^{x}=n.}$

Графік log₂x як функції додатних дійсних чисел x

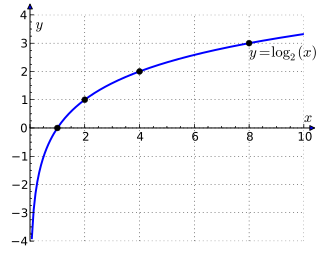
Наприклад, двійковий логарифм числа 1 дорівнює 0, двійковий логарифм числа 2 — 1, двійковий логарифм числа 4 дорівнює 2, а двійковий логарифм числа 32 — 5.

Означення та позначення

Бінарний логарифм — це логарифм за основою 2. Функція двійкового логарифма є оберненою функцією до функції степеня двійки. Окрім стандартного позначення log₂, використовуються альтернативні позначення, такі як lg, ld, lb та log (за попередньої домовленості, що основою є 2).

Історично перше застосування двійкових логарифмів сталося в теорії музики. Леонард Ейлер використовував їх для визначення кількості октав, на які відрізняються два музичних тони. Двійкові логарифми можна застосувати для розрахунку довжини представлення числа в двійковій системі числення, або для визначення кількість бітів, необхідних для кодування повідомлення в теорії інформації. У комп'ютерних науках двійкові логарифми використовуються для підрахунку кількості кроків, які потрібно виконати при двійковому пошуку і подібних алгоритмах. Інші галузі застосування — цекомбінаторика, біоінформатика, планування спортивних турнірів, і фотографія.

Двійкові логарифми входять до стандартних математичних функцій мови програмування C та є частиною багатьох математичних програмних пакетів.

Цілу частину двійкового логарифма можна визначити через пошук першої одиниці у двійковому поданні цілого числа або через пошук експоненти значення з рухомою комою.

Історія

Докладніше: Історія логарифмів

Леонард Ейлер був першим, хто застосував двійкові логарифми в теорії музики, у 1739.

Степені двійки були відомі і використовувалися ще з античних часів; наприклад вони є в Euclid's Elements, Книга IX.32 (про факторизацію степенів двійки) і IX.36 (в частині Евклідово-Ейлерової теореми^[en], про структуру парних досконалих чисел). А двійковий логарифм степеня двійки позначав позицію в упорядкованій послідовності степенів двійки.

На цій основі, Михаель Штифель створив і опублікував першу відому таблицю двійкових логарифмів в 1544. Його книга Arthmetica Integra містила декілька таблиць, які впорядковували цілі числа із відповідними їхніми степенями двійки. Якщо розвернути навпаки рядки цих таблиць їх можна інтерпретувати як таблиці двійкових логарифмів.^[1][2]

Раніше за Штифеля, у 8-му столітті Джайнійському математику Вірасена^[en] створив попередника двійкового логарифма. Концепція Вірасена, що називалася ardhacheda визначалася як кількість разів, при яких задане число можна поділити порівну на два. Це визначення приводить до функції, яка за змістом збігається з двійковим логарифмом за основою два,^[3] але відрізняється для інших цілих, і дає 2-адичний порядок^[en], а не логарифм.^[4]

Сучасна форма двійкового логарифма, що застосовується до будь-якого числа (не лише степені двійки) була в явному вигляді розглянута Леонардом Ейлером в 1739. Ейлер започаткував використання двійкових логарифмів в теорії музики, задовго до їхнього більш значимого використання в теорії інформації і комп'ютерних науках. Як частину своєї роботи в цій сфері, Ейлер опублікував таблицю логарифмів для цілих чисел від 1 до 8, з точністю до сьомого десяткового знаку точності.^[5][6]

Визначення і властивості

Функцію двійкового логарифма можна визначити як обернену функцію від функції степені двійки, що строго зростає в області додатних дійсних чисел і таким чином має одну єдину зворотню функцію.^[7] Альтернативним шляхом, її можна визначити як ln n/ln 2, де ln є натуральним логарифмом, визначений одним із своїх стандартних способів. Використання комплексного логарифма в такому визначення дозволяє розширити застосування двійкового логарифма для комплексних чисел.^[8]

Як і для інших логарифмів, двійковий логарифм задовольняє наступним рівнянням, які можуть використовуватись для спрощення формул, які поєднують двійкові логарифми із множенням або зведенням в ступінь:^[9]

${\displaystyle \log _{2}xy=\log _{2}x+\log _{2}y}$

${\displaystyle \log _{2}{\frac {x}{y}}=\log _{2}x-\log _{2}y}$

${\displaystyle \log _{2}x^{y}=y\log _{2}x.}$

Застосування

Теорія інформації

Кількість розрядів (біт) в двійковому представленні додатного цілого n дорівнюватиме цілій частині числа 1 + log₂n.^[10]

${\displaystyle \lfloor \log _{2}n\rfloor +1.\,}$

В теорії інформації, визначення кількості власної інформації та інформаційна ентропія часто задаються за допомогою двійкового логарифма, тим самим представляючи біт як фундаментальну одиницю інформації. Однак, в альтернативних представленнях цих визначень також використовують натуральний логарифм і нат.^[11]

Комбінаторика

Хоча натуральний логарифм є більш важливим ніж двійковий логарифм для багатьох галузей чистої математики, таких як теорія чисел і математичний аналіз,^[12] двійковий логарифм має ряд застосувань в комбінаториці:

• Кожне двійкове дерево кожне n листя має висоту принаймні в log₂n, і стає рівним цьому значенню, коли n є степенем двійки, а саме дерево є повним двійковим деревом.^[13] Відповідно, число Стрехлера річкової системи із n притоками буде щонайбільше дорівнювати log₂n + 1.^[14]
• Кожне сімейство множин з n різними наборами має принаймні log₂n елементів в купі, і буде рівністю коли це сімейство становить булеан.^[15]
• Кожен частковий куб із n вершинами має ізометричну розмірність щонайменше в log₂n, і має не більше ніж 1/2 n log₂n ребер, при чому рівність буде, якщо частковий куб є графом гіперкуба.^[16]
• Відповідно до Теореми Рамсея, кожний неорієнтований граф з n-вершин має або кліку або незалежну множину з розміром в логарифмічній залежності із n. Точний розмір гарантовано не відомий, але найкраща відома межа цього розміру застосовує двійковий логарифм. Зокрема, всі графи мають кліку або незалежну множину розміром принаймні в 1/2 log₂n (1 − o(1)) і майже всі графи не мають кліки або незалежної множини більшого розміру ніж 2 log₂n (1 + o(1)).^[17]
• Із теорії математичного аналізу модель Гільберта-Шеннона-Рідса^[en] для випадкового тасування кар, можна визначити число разів необхідних при тасуванні колоди з n-карт, використовуючи метод каскадного тасування, аби отримати кількість перестановок, що будуть близкі до рівномірного розподілу, і це значення приблизно дорівнює 3/2 log₂n. Цей підрахунок дав основу для рекомендації, що колода з 52-карт повинна перемішуватись сім разів.^[18]

Обчислювальна складність

Двійковий пошук в відсортованому масиві, часова складність алгоритму розраховується за допомогою двійкових логарифмів

Двійковий логарифм також часто фігурує в аналізі алгоритмів, не тільки через часте використання двійкової арифметики в алгоритмах, а й тому, що двійкові логарифми зустрічаються при аналізі алгоритмів, заснованих на двонаправлених розгалуженнях.^[19] Якщо задача початково має n варіантів шляху вирішення, а кожна ітерація алгоритму зменшує кількість варіантів в два рази, тоді кількість ітерацій, необхідних аби завершити пошук на одному з варіантів знову таки є цілою частиною від log₂n. Цей підхід використовується при аналізі багатьох алгоритмів і структур даних. Наприклад, при двійковому пошуку, об'єм задачі, що розв'язується зменшується навпіл при кожній ітерації, і таким чином приблизно log₂n ітерацій необхідно здійснити або отримати задачу розміром 1, що означає, що задачу можна вирішити за скінченний передбачений час.^[20] Аналогічно, ідеально збалансоване дерево двійкового пошуку, яке містить n елементів має висоту log₂(n + 1) − 1.^[21]

Час роботи алгоритму зазвичай виражають в нотації Ландау (велике О), яка використовується для спрощення виразів не указуючи постійних складових і членів нижчого порядку. Оскільки логарифми з різними основами відрізняються один від одного лише на сталу величину, про алгоритми, які виконуються за час O(log₂n) також можна казати, що вони виконуються за O(log₁₃ n) часу. Основу логарифма у виразах такого вигляду як O(log n) або O(n log n) можна не вказувати.^[22][23] Однак, якщо логарифм вказується в показнику степеня при розрахунку часу, основою логарифма не можна нехтувати і треба вказувати. Наприклад, O(2^log₂n) не те саме, що O(2^{ln n}) оскільки останнє буде дорівнювати O(n) а перший вираз — O(n^0.6931...).

Алгоритми з часом виконання O(n log n) іноді називають лінійно-логарифмічними.^[24] Прикладами алгоритмів із часом виконання O(log n) або O(n log n) є:

• Швидке сортування і інші алгоритми сортування порівняннями^[25]
• Пошук в збалансованому двійковому дереві пошуку^[26]
• Швидке піднесення до степеня^[27]
• Задача пошуку найбільшої зростаючої підпослідовності^[28]

Теорія музики

В теорії музики, інтервал або різниця сприйняття між двома тонами визначається відношенням їх частот. Інтервали, що утворені за допомогою співвідношення раціональних чисел із малими чисельниками і знаменниками сприймаються особливо милозвучно. Найпростішим і найважливішим із таких інтервалів є октава, що має співвідношення частот 2:1. Кількість октав, на які відрізняються звукові тони дорівнюють двійковому логарифму від співвідношення їх частот.^[29]

При вивченні музичного строю і інших аспектів музичної теорії, які потребують кращого розрізнення між тонами, ж зручним мати міру розміру інтервалу меншу за октаву із властивістю адитивності (чим є логарифми), а не мультиплікативності (яким є співвідношення частот). Таким чином, якщо тони x, y, і z утворюють зростаючу послідовність тонів, то міра інтервалу від x до y плюс міра інтервалу від y до z повинні дорівнювати мірі інтервалу від x до z. Така міра задається за допомогою центу, який поділяє октаву на 1200 рівних інтервалів (12 півтонів, що містять 100 центів кожен). Математично, якщо дані тони із частотами f₁ і f₂, кількість центів в інтервалі від f₁ до f₂ становитиме^[29]

${\displaystyle \left|1200\log _{2}{\frac {f_{1}}{f_{2}}}\right|.}$

Міліоктава^[en] визначається тим самим способом, але матиме множник 1000 замість 1200.^[30]

Фотографія

У фотографії, значення експозиції^[en] вимірюється як двійковий логарифм від кількості світла, яке досягає плівки або сенсору зображення, у відповідності до закону Вебера-Фехнера, який описує логарифмічний характер сприйняття світла зоровою системою людини. Один крок зміни експозиції є однією одиницею логарифмічної шкали за основою-2.^[31][32] Більш точно, значення експозиції фотографії визначається як

${\displaystyle \log _{2}{\frac {N^{2}}{t}}}$

де N це f-число діафрагми, яке вимірює апертуру лінзи під час експозиції, а t це тривалість експозиції в секундах.^[33]

Двійкові логарифми також використовуються в денситометрії, щоб оцінити динамічний діапазон світлочутливого матеріалу або цифрового сенсора.^[34]

Обчислення

Інженерний калькулятор TI SR-50 (1974). Кнопки ln і log знаходяться в другому рядку; немає кнопки log₂.

Перетворення із інших основ

Простим способом розрахувати значення log₂n на калькуляторі, який не має функції log₂, це використати натуральний логарифм (ln), звичайний логарифм (log або log₁₀), які можна знайти в багатьох інженерних калькуляторах^[en]. Для цього існує формула зміна основи логарифма:^[32][35]

${\displaystyle \log _{2}n={\frac {\ln n}{\ln 2}}={\frac {\log _{10}n}{\log _{10}2}},}$

або наближено

${\displaystyle \log _{2}n\approx 1.442695\ln n\approx 3.321928\log _{10}n.}$