Квадратний корінь з двох

Квадратний корінь з числа 2 — дійсне число більше нуля, яке при множенні саме на себе дає число 2. Позначення: ${\displaystyle {\sqrt {2}}.}$ Приведемо значення кореня з 2 з 65 знаками після коми:

1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…

Квадратний корінь з 2 дорівнює довжині гіпотенузи в прямокутному трикутнику з довжиною катетів 1.

Геометричний корінь з 2 можливо представити як довжину діагоналі квадрата зі стороною 1 (це слідує з теореми Піфагора). Можливо, це було перше відоме в історії математики ірраціональне число (тобто число, яке неможливо точно представити у вигляді дробу).

Квадратний корінь з 2.

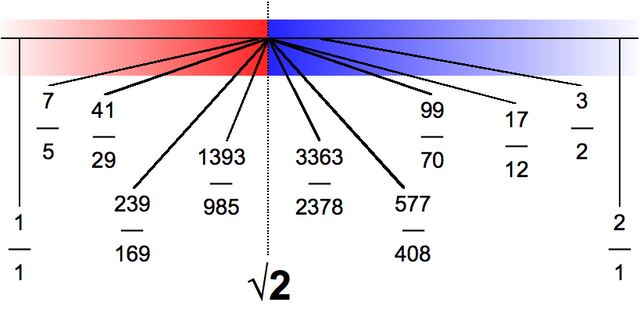
Гарним і часто використовуваним наближенням до ${\displaystyle {\sqrt {2}}}$ є дріб ${\displaystyle {\tfrac {99}{70}}}$. Незважаючи на те, що чисельник і знаменник дробу лише двозначні цілі, воно відрізняється від реального значення менше, ніж на 1/10000.

Ірраціональне число √2
Система числення	Запис числа √2
Двійкова	1.0110101000001001111…
Десяткова	1.4142135623730950488…
Шістнадцяткова	1.6A09E667F3BCC908B2F…
Ланцюговий дріб	${\displaystyle 1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}}}}$

Історія

Вавилонська глиняна табличка з максимально точним зазначенням довжини діагоналі одиничного квадрата чотиризначним шістдесятковим числом.

Вавилонська глиняна табличка (1900 до н. е. — 1650 до н. е.) дає найточніше наближене значення ${\displaystyle {\sqrt {2}}}$ при записі в чотирьох шістдесяткових цифрах, що після округлення становить 6 точних десяткових цифр:

${\displaystyle 1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}=1.41421{\overline {296}}.}$^[1]

Інше раннє наближення цього числа в давньоіндійському математичному тексті, Шульба-сутри (бл. 800–200 до н. е.) дається наступним чином:

${\displaystyle 1+{\frac {1}{3}}+{\frac {1}{3\cdot 4}}-{\frac {1}{3\cdot 4\cdot 34}}={\frac {577}{408}}\approx 1.414215686.}$

Піфагорійці виявили, що діагональ квадрата непорівнянна з його стороною, або сучасною мовою, що квадратний корінь з двох є ірраціональним. Мало що відомо з певністю про час і обставини цього видатного відкриття, але традиційно його авторство приписується Гіппасу Метапонтському, якого за це відкриття, за різними варіантами легенди, піфагорійці не то вбили, не то вигнали, поставивши йому в провину руйнування головної піфагорейської доктрини про те, що «все є натуральне число». Тому квадратний корінь з 2 іноді називають постійною Піфагора, через те, що саме піфагорійці довели його ірраціональність, тим самим відкривши існування ірраціональних чисел.

Алгоритми обчислення

Існує безліч алгоритмів для обчислення значення квадратного кореня з двох. В результаті алгоритму виходить приблизне значення ${\displaystyle {\sqrt {2}}}$ у вигляді звичайної або десяткового дробу. Найпопулярніший алгоритм для цього, який використовується в багатьох комп'ютерах і калькуляторах, це вавилонський метод обчислення квадратних коренів. Він полягає в наступному:

${\displaystyle a_{n+1}={\frac {a_{n}+{\frac {2}{a_{n}}}}{2}}={\frac {a_{n}}{2}}+{\frac {1}{a_{n}}}.}$

Чим більше повторень в алгоритмі (тобто, чим більше «n»), тим краще наближення квадратного кореня з двох. Кожне повторення приблизно подвоює кількість правильних цифр. Наведемо кілька перших наближень:

• 3/2 = 1.5
• 17/12 = 1.416…
• 577/408 = 1.414215…
• 665857/470832 = 1.4142135623746…

У 1997 році Ясумаса Канада вирахував значення √2 до 137 438 953 444 десяткових знаків після коми. У лютому 2007 року рекорд був побитий: Сігеру Кондо вирахував 200 мільярдів десяткових знаків після коми протягом 13 днів і 14 годин, використовуючи процесор з частотою 3,6 ГГц і 16 гігабайт оперативної пам'яті. Серед математичних констант тільки ${\displaystyle \pi }$ було обчислено більш точно.

Властивості квадратного кореня з двох

Половина √2 приблизно дорівнює 0.70710 67811 86548; ця величина дає в геометрії та тригонометрії координати одиничного вектора, який утворює кут 45° з координатними осями:

${\displaystyle {\frac {\sqrt {2}}{2}}={\sqrt {\frac {1}{2}}}={\frac {1}{\sqrt {2}}}=\cos(45^{\circ })=\sin(45^{\circ }).}$

Одна з цікавих властивостей √2 полягає в наступному:

${\displaystyle \!\ {1 \over {{\sqrt {2}}-1}}={\sqrt {2}}+1}$. Тому що ${\displaystyle ({\sqrt {2}}+1)({\sqrt {2}}-1)=2-1=1.}$

Це є результатом властивості срібного перетину.

Друга цікава властивість √2:

${\displaystyle {\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots }}}}}}=2.\,}$

Квадратний корінь з двох може бути виражений в уявних одиницях ${\displaystyle i}$, використовуючи тільки квадратні корені і арифметичні операції:

${\displaystyle {\frac {{\sqrt {i}}+i{\sqrt {i}}}{i}}}$ і ${\displaystyle {\frac {{\sqrt {-i}}-i{\sqrt {-i}}}{-i}}.}$

Квадратний корінь з 2 є єдиним числом, відмінним від 1, чия нескінченна тетрація дорівнює його квадрату.

${\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\ \cdot ^{\cdot ^{\cdot }}}}}=2}$

Квадратний корінь з двох може бути також використаний для наближення ${\displaystyle \pi }$:

${\displaystyle 2^{m}{\sqrt {2-{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}}\to \pi \ (m\to \infty )}$^[2]

З точки зору вищої алгебри, ${\displaystyle {\sqrt {2}}}$ є коренем многочлена ${\displaystyle x^{2}-2}$ і тому є цілим алгебраїчним числом. Множина чисел виду ${\displaystyle a+b{\sqrt {2}}}$, де ${\displaystyle ~a,b}$ — раціональне число, створює алгебраїчне поле. Воно позначається ${\displaystyle \mathbb {Q} [{\sqrt {2}}]}$ і є підполем поля дійсних чисел.

Доказ ірраціональності

Застосуємо доказ від протилежного: нехай, ${\displaystyle {\sqrt {2}}}$ раціональний, тобто представляється у вигляді дробу ${\displaystyle {\frac {m}{n}}}$, де ${\displaystyle m}$ і ${\displaystyle n}$ — цілі числа. Піднесемо рівність в квадрат:

${\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}}$.

Так як m² містить парне число двійок, а 2n² — непарне число двійок, отже рівність m²=2n² неможлива. Це означає, що вихідне припущення було невірним, і ${\displaystyle {\sqrt {2}}}$ — ірраціональне число.

Ланцюговий дріб

Квадратний корінь з двох може бути представлений у вигляді ланцюгового дробу:

${\displaystyle \!\ {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}}}.}$

Відповідні дроби даного ланцюгового дробу дають наближені значення, швидко сходяться до точного квадратного кореня з двох. Спосіб їх обчислення простий: якщо позначити попередній відповідний дріб ${\displaystyle {\frac {m}{n}}}$, то подальший має вигляд ${\displaystyle {\frac {m+2n}{m+n}}}$. Швидкість збіжності тут менше, ніж у методу Ньютона, але обчислення набагато простіше. Випишемо декілька перших наближень:

${\displaystyle {\frac {3}{2}};\ {\frac {7}{5}};\ {\frac {17}{12}};\ {\frac {41}{29}};\ {\frac {99}{70}};\ {\frac {239}{169}};\ {\frac {577}{408}};\ {\frac {1393}{985}};\ {\frac {3363}{2378}}\dots }$

Квадрат останнього наведеного дробу дорівнює (округлено) 2,000000177.

Розмір паперу

Квадратний корінь з двох є пропорцією формату паперу ISO 216. Співвідношення сторін таке, що при розрізанні аркуша навпіл, паралельно його короткій стороні, вийдуть два аркуша тієї ж пропорції. Це дозволяє нумерувати такі, найуживаніші формати паперу, одним числом, згідно з геометричним зменшенням площі листа (відповідно числу розрізів) — А0, А1, А2, А3, А4,…

Див. також

• Ірраціональність
• Теорема Вієта