Опуклий аналіз

Опуклий аналіз — це гілка математики, присвячена вивченню властивостей опуклих функцій і опуклих множин, часто застосовується в опуклому програмуванні, підгалузі теорії оптимізації.

3-вимірний опуклий многогранник. Опуклий аналіз включає не тільки вивчення опуклих підмножин евклідових просторів, але й вивчення опуклих функцій на абстрактних просторах.

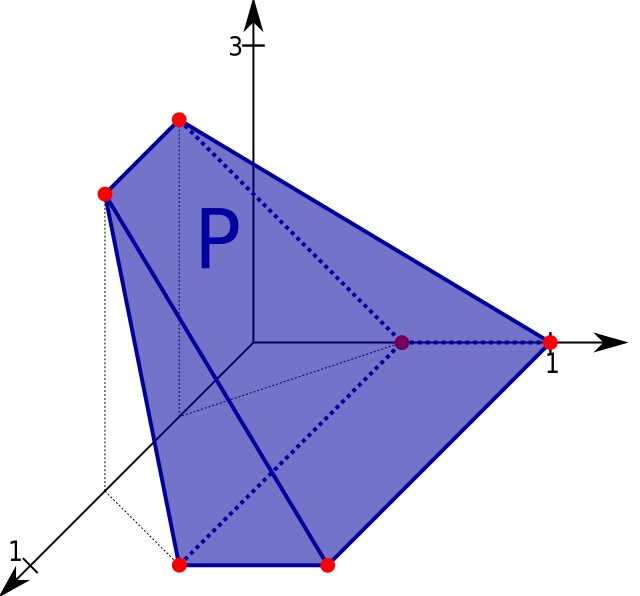
Опуклі множини

Опукла множина — це множина ${\displaystyle C\subseteq X}$ для деякого векторного простору X, така що для будь-яких ${\displaystyle x,y\in C}$ і ${\displaystyle \lambda \in [0,1]}$^[1]

${\displaystyle \lambda x+(1-\lambda )y\in C}$.

Опукла функція

Опукла функція — це будь-яка розширена дійснозначна функція ${\displaystyle f:X\to \mathbb {R} \cup \{\pm \infty \}}$, яка задовольняє нерівності Єнсена, тобто, для будь-яких ${\displaystyle x,y\in X}$ і будь-якого ${\displaystyle \lambda \in [0,1]}$

${\displaystyle f(\lambda x+(1-\lambda )y)\leqslant \lambda f(x)+(1-\lambda )f(y)}$^[1].

Еквівалентно, опуклою функцією є будь-яка (розширена) дійснозначна функція, така що її надграфік

${\displaystyle \left\{(x,r)\in X\times \mathbf {R} :f(x)\leqslant r\right\}}$

є опуклою множиною^[1].

Опукле спряження

Опукле спряження розширеної (не обов'язково опуклої) функції ${\displaystyle f:X\to \mathbb {R} \cup \{\pm \infty \}}$ — це функція ${\displaystyle f^{*}:X^{*}\to \mathbb {R} \cup \{\pm \infty \}}$, де X* — спряжений простір простору X^[2], така що

${\displaystyle f^{*}(x^{*})=\sup _{x\in X}\left\{\langle x^{*},x\rangle -f(x)\right\}.}$

Подвійне спряження

Подвійне спряження функції ${\displaystyle f:X\to \mathbb {R} \cup \{\pm \infty \}}$ — це спряження спряження, що зазвичай записують як ${\displaystyle f^{**}:X\to \mathbb {R} \cup \{\pm \infty \}}$. Подвійне спряження корисне, коли потрібно показати, що виконується сильна або слабка двоїстість (за допомогою функції збурень^[en]).

Для будь-кого ${\displaystyle x\in X}$ нерівність ${\displaystyle f^{**}(x)\leqslant f(x)}$ випливає з нерівності Фенхеля. Для власної функції^[en] f = f** тоді й лише тоді, коли f опукла і напівнеперервна знизу за теоремою Фенхеля — Моро^[2][3].

Опукла мінімізація

(Пряма) задача опуклого програмування, це задача вигляду

${\displaystyle \inf _{x\in M}f(x)}$

така що ${\displaystyle f:X\to \mathbb {R} \cup \{\pm \infty \}}$ є опуклою функцією, а ${\displaystyle M\subseteq X}$ є опуклою множиною.

Двоїста задача

Принцип двоїстості в оптимізації стверджує, що задачу оптимізації можна розглядати з двох точок зору як пряму задачу або двоїсту задачу.

Загалом, якщо дано двоїсту пару^[en][4] відокремлюваних локально опуклих просторів ${\displaystyle \left(X,X^{*}\right)}$ та функцію ${\displaystyle f:X\to \mathbb {R} \cup \{+\infty \}}$, можна визначити пряму задачу як знаходження такого ${\displaystyle {\hat {x}}}$, що ${\displaystyle f({\hat {x}})=\inf _{x\in X}f(x).\,}$ Іншими словами, ${\displaystyle f({\hat {x}})}$ — це інфімум (точна нижня границя) функції ${\displaystyle f}$.

Якщо є обмеження, їх можна вбудувати у функцію ${\displaystyle f}$, якщо покласти ${\displaystyle {\tilde {f}}=f+I_{\mathrm {constraints} }}$, де ${\displaystyle I}$ — індикаторна функція^[en]. Нехай тепер ${\displaystyle F:X\times Y\to \mathbb {R} \cup \{+\infty \}}$ (для іншої двоїстої пари ${\displaystyle \left(Y,Y^{*}\right)}$) — функція збурень^[en], така що ${\displaystyle F(x,0)={\tilde {f}}(x)}$^[5].

Двоїста задача для цієї функції збурення відносно вибраної задачі визначається як

${\displaystyle \sup _{y^{*}\in Y^{*}}-F^{*}(0,y^{*})}$

де F* — опукле спряження за обома змінними функції F.

Розрив двоїстості — це різниця правої та лівої частин нерівності

${\displaystyle \sup _{y^{*}\in Y^{*}}-F^{*}(0,y^{*})\leqslant \inf _{x\in X}F(x,0),\,}$

де ${\displaystyle F^{*}}$ — опукле спряження від обох змінних, а ${\displaystyle \sup }$ означає супремум (точна верхня границя)^[6][7][5][6] .

${\displaystyle \sup _{y^{*}\in Y^{*}}-F^{*}(0,y^{*})\leqslant \inf _{x\in X}F(x,0).}$

Цей принцип збігається зі слабкою двоїстістю. Якщо обидві сторони рівні, кажуть, задача задовольняє умовам сильної двоїстості.

Існує багато умов для сильної двоїстості, такі як:

• F = F**, де F — функція збурень^[en] для прямої та двоїстої задач, а F** — подвійне спряження функції F;
• пряма задача є задачею лінійного програмування;
• Умова Слейтера для задач опуклого програмування^[8][9].

Двоїстість Лагранжа

Для опуклої задачі мінімізації з обмеженнями-нерівностями

${\displaystyle \min _{x}f(x)}$ за умов ${\displaystyle g_{i}(x)\leqslant 0}$ для i = 1, …, m .

двоїстою задачею Лагранжа буде

${\displaystyle \sup _{u}\inf _{x}L(x,u)}$ за умов ${\displaystyle u_{i}(x)\geqslant 0}$ для i = 1, …, m ,

де цільова функція${\displaystyle L(x,u)}$ є двоїстою функцією Лагранжа, визначеною так:

${\displaystyle L(x,u)=f(x)+\sum _{j=1}^{m}u_{j}g_{j}(x)}$