Перелік картографічних проєкцій

Цей перелік/таблиця дає огляд найбільш значущих картографічних проєкцій. Список не може бути повним, так як не існує обмежень на кількість можливих картографічних проєкцій^[1].

Цей список незавершений, Ви можете допомогти — додати пункти, яких бракує.

Таблиця проєкцій

Проєкція	Зображення	Тип	Властивості	Застовував	Рік	Примітки
Прямокутна = еквідистантна циліндрична = прямокутна = la carte parallélogrammatique		Циліндрична	Еквідистантна	Марін Тірський	120 (бл.)	Найпростіша геометрія; відстані уздовж меридіанів зберігаються. Плаский квадрат: спеціальний випадок, що має екватор як звичайну паралель.
Проєкція Кассіні[en] = Кассіні-Солднер		Циліндрична	Еквідистантна	Цезар-Франсуа Кассіні де Тюрі	1745	Поперечна еквідистантна проєкція; відстані уздовж центрального меридіана зберігаються. Distances perpendicular to central meridian are preserved.
Меркатор = Райт		Циліндрична	Рівнокутна	Герард Меркатор	1569	Лінії постійної орієнтації (лінії румбів) прямі, що зручно при навігації. Площі на стільки розтягуються з широтою, що карта не здатна показати полюси.
Вебмеркатор[en]		Циліндрична	Компромісна	Google	2005	Варіація проєкції Меркатора. Де-факто стандарт для картографічних вебдодатків, що використовується всіма основними постачальниками онлайн карт, включаючи Google Maps, Bing Maps, Mapquest, Mapbox, OpenStreetMap та інші.
Гаус–Крюгер = Рівнокутна Гауса = (Еліпсоїдальна) Поперечна проєкція Меркатора		Циліндрична	Рівнокутна	Карл Фрідріх Гаус Іоганн Генріх Луї Крюгер	1822	Ця поперечна, еліпсоїдальна форма проєкції Меркатора є скінченною, на відміну від екваторіальної версії. Формує основу UTM системи.
Стереографічна проєкція Галла схожий на Браун		Циліндрична	Компромісна	Джеймс Галл	1885	Намагався бути схожим на Меркатора, в той же час показувати полюси. Стандартні паралелі на 45°N/S. Браун — горизонтально натягнута версія зі шкалою правильною на екваторі.
Міллер = циліндричний Міллер		Циліндрична	Компромісна	Осборн Мейтленд Міллер	1942	Намагався бути схожим на Меркатора, в той же час показувати полюси.
Рівновелика циліндрична Ламберта		Циліндрична	Рівновелика	Йоганн Генріх Ламберт	1772	Стандартний паралельний на екваторі. Співвідношення сторін π (3.14). Базова проєкція з сім'ї Циліндричних рівних площ.
Берманн		Циліндрична	Рівновелика	Вальтер Берманн	1910	Горизонтально стиснута версія рівновеликої Ламберта. Має стандартні паралелі на 30°N/S і співвідношення сторін 2.36.
Гобо-Даєр		Циліндрична	Рівновелика	Мік Даєр	2002	Горизонтально стиснута версія рівновеликої Ламберта. Дуже схожими є Трістан Едвардс і рівна поверхня Сміта (= прямокутна Крастера) Проєкції з стандартними паралелями на позначці 37°N/S. Співвідношення сторін ~2.0.
Галл-Петерс = ортографічний Галл = Петерс		Циліндрична	Рівновелика	Джеймс Галл (Арно Петерс)	1855	Горизонтально стиснута версія рівновеликої Ламберта. Стандартні паралелі на 45°N/S. Співвідношення сторін ~1.6. Схожою є проєкція Бальтазара зі стандартними паралелями на 50°N/S.
Синусоїдальна = Сансон-Флемстид = рівновеликий Меркатор		Псевдо-циліндрична	Рівновелика	(Декілька; перший невідомий)	1600 (бл.)	Меридіани є синусоїдами; паралелі рівновіддалені. Співвідношення сторін 2:1. Відстані уздовж паралелей зберігаються.
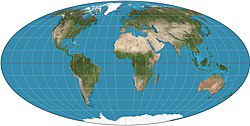
Мольвейде = еліптична = Бабіне = гомолографічна		Псевдо-циліндрична	Рівновелика	Карл Брандан Мольвейде	1805	Меридіани це еліпси.
Еккерт II		Псевдо-циліндрична	Рівновелика	Макс Еккерт-Грейфендорфф	1906
Еккерт IV		Псевдо-циліндрична	Рівновелика	Макс Еккерт-Грейфендорфф	1906	Паралелі мають не однакові відстані і масштаби; крайні меридіани мають форму півкола; інші меридіани являють собою майже еліпси.
Еккерт VI		Псевдо-циліндрична	Рівновелика	Макс Еккерт-Грейфендорфф	1906	Паралелі мають неоднакові відстані і масштаби; меридіани являють собою пів-періоди синусоїд.
Перервна Гуда		Псевдо-циліндрична	Рівновелика	Джон Пол Гуд	1923	Гібрид синусоїдальної і проєкції Мольвейде. Зазвичай використовується у вигляді проєкції з розривами.
Каврайський VII		Псевдо-циліндрична	Компромісна	Володимир Каврайський	1939	Рівномірно розподілені паралелі. Еквівалент до Вагнер VI стиснутої по горизонталі на коефіцієнт ${\displaystyle {\sqrt {3}}/{2}}$.
Робінсон		Псевдо-циліндрична	Компромісна	Артур Робінсон	1963	Розрахована шляхом інтерполяції табличних значень. Використовувалась Рендом МакНеллі з моменту створення і використовувалась NGS 1988–98.
Природна Земля		Псевдо-циліндрична	Компромісна	Том Паттерсон	2011	Розрахована шляхом інтерполяції табличних значень.
Гіпереліптична Тоблера		Псевдо-циліндрична	Рівновелика	Валдо Р. Тоблер	1973	Сім'я картографічних проєкцій, що включає в себе як окремий випадок проєкцію Мольвейде, проєкцію Колліньона, і різні циліндричні проєкції рівних площ.
Вагнер VI		Псевдо-циліндрична	Компромісна	K.H. Вагнер	1932	Еквівалент до Каврайський VII вертикально стиснутої на коефіцієнт ${\displaystyle {\sqrt {3}}/{2}}$.
Колліньон		Псевдо-циліндрична	Рівновелика	Едуард Колліньон	1865 (бл.)	Залежно від конфігурації, проєкція також може відображати сферу до одного алмазу або пару квадратів.
HEALPix		Псевдо-циліндрична	Equal-area	Кшиштоф М. Горський	1997	Гібрид з Колліньон + Ламберт циліндричних рівновеликих
Єсморфічна Боггса		Псевдо-циліндрична	Рівновелика	Сємюель Уітмор Боггс	1929	Рівновелика проєкція, що є результатом з середнього синусоїдальної і Мольвейде y-координат і тим самим обмежує x координати.
Параболічна проєкція Крастера =Путнінс П4		Псевдо-циліндрична	Рівновелика	Джон Крастер	1929	Меридіани являють собою параболи. Стандартні паралелі на 36°46′N/S; паралелі неоднорідні у інтервалах і розмірах; відношення сторін 2:1.
Пласка-полярна четвертого ступеню = МакБрайд-Томас #4		Псевдо-циліндрична	Рівновелика	Фелікс В. МакБрайд, Пол Томас	1949	Стандартні паралелі на 33°45′N/S; паралелі неоднорідні у інтервалах і розмірах; меридіани є кривими четвертого порядку. Не має спотворень лише там, де стандартні паралелі перетинають центральний мередіан.
Авталік четвертого ступеню		Псевдо-циліндрична	Рівновелика	Карл Сеймон Оскар Адамс	1937 1944	Паралелі неоднорідні у інтервалах і розмірах. Не має спотворень вздовж екватора. Меридіани являють собою криві четвертого порядку.
Таймс		Псевдо-циліндрична	Компромісна	Джон М'юїр	1965	Стандартні паралелі 45°N/S. Паралелі базуються на ортографічному Галлі, але з вигнутими мередіанами. Розроблена для Bartholomew Ltd., The Times Atlas.
Локсимутальна		Псевдо-циліндрична		Карл Сеймон, Валдо Тоблер	1935, 1966	З визначеного центру, ліній постійного обертання (румби/локсодроми) прямі і мають правильну довжину. Взагалі асиметрична щодо екватора.
Аітофф		Псевдо-азимутна	Компромісна	Девід А. Аітофф	1889	Розтягування зміненої екваторіальної азимутальної еквідистантної мапи. Границя являє собою 2:1 еліпс. В значній мірі замінена Хаммером.
Хаммер = Хаммер-Аітофф варіації: Брейсмейстер; Нордік		Псевдо-азимутна	Рівновелика	Ернст Хаммер	1892	Змінена з азимутальної рівновеликої мапи. Границя являє собою 2:1 еліпс. Варіантами є похилі версії, центровані на 45°N.
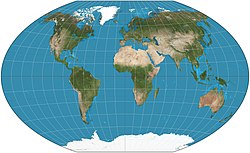
Потрійна Вінкеля		Псевдо-азимутна	Компромісна	Освальд Вінкель	1921	Арифметичне значення проєкції рівних прямокутників і проєкції Аітоффа. Стандартна проєкція світу для NGS 1998–сьогодення.
Проєкція Ван дер Ґрінтена		Інша	Компромісна	Альфонс Й. ван дер Грінтен	1904	Границя є колом. Всі паралелі і меридіани є дугами кіл. Зазвичай обрізається близько 80°N/S. Стандартна проєкція світу NGS 1922-88.
Еквідистантна конічна проєкція = проста конічна		Конічна	Еквідистантна	Заснована на першій проєкції Птолемея	100 (бл.)	Відстані уздовж меридіанів зберігаються, як відстані уздовж однієї або двох стандартних паралелей.[2]
Рівнокутна конічна Ламберта		Конічна	Рівнокутна	Йоганн Генріх Ламберт	1772
Конічна Альберса		Конічна	Рівновелика	Генріх С. Альберс	1805	Дві стандартні паралелі з низьким рівнем спотворень між ними.
Вернер		Псевдо-конічна	Рівновелика	Йоганнес Стабіус	1500 (бл.)	Відстань від північного полюсу правильна, як і вигнуті відстані уздовж паралелей.
Бонне		Псевдо-конічна, серцеподібна	Рівновелика	Бернардус Сильванус	1511	Паралелі являють собою рівномірно розподілені кругові дуги і стандартні лінії. Зовнішній вигляд залежить від опорної паралелі. Загальний випадок як Вернера і синусоїдальної.
Боттомлі		Псевдо-конічна	Рівновелика	Генрі Боттомлі	2003	Альтернатива проєкції Бонне з простішою загальною формою. Паралелі являють собою еліптичні дуги Зовнішній вигляд залежить від опорної паралелі.
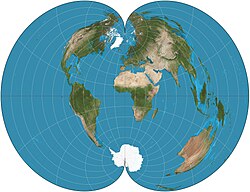
Американська поліконічна		Псевдо-конічна		Фердинанд Рудольф Хесслер	1820 (бл.)	Відстані уздовж паралелей зберігаються, як і відстані уздовж центрального меридіана.
Азимутна еквідистантна =Постіль зенітна еквідистантна		Азимутна	Еквідистантна	Абу Райхан ал-Біруні	1000 (бл.)	Використана USGS у Національному атласі Сполучених Штатів Америки. Відстані від центру зберігаються. Використовується як емблема Організації Об'єднаних Націй, з поширенням до 60° S.
Гномонічна		Азимутна	Гномонічна	Фалес (можливо)	580 до н. е. (бл.)	Всі великі кола вкладаються у прямі лінії. Екстремальні спотворення далеко від центру. Показує менше, ніж одну півкулю.
Рівновелика азимутна Ламберта		Азимутна	Рівновелика	Йоганн Генріх Ламберт	1772	Відстань по прямій лінії між центральною точкою на карті та будь-якою іншою точкою є такою ж, як лінійна тривимірна відстань через земну кулю між двома точками.
Стереографічна		Азимутна	Рівнокутна	Гіппарх (застосував)	200 до н. е. (бл.)	Мапа нескінченна в обводі з зовнішньою півкулею серйозно роздувається, тому вона часто використовується як дві півкулі. Відображає всі маленькі кола на окружності, які корисні для планетарного відображення, щоб зберегти форму кратерів.
Ортографічна[en]		Азимутна		Гіппарх (застосував)	200 до н. е. (бл.)	Вигляд з нескінченної відстані.
Вертикальна перспектива		Азимутна		Маттіас Зойттер (застосував)	1740	Вигляд з скінченної відстані. Може відобразити лише менше півкулі.
Дво-точкова еквідистантна		Азимутна	Еквідистантна	Ханс Маурер	1919	Дві «контрольні точки» можуть бути майже довільними. Два прямолінійні відстані з будь-якої точки на карті до двох контрольних точок правильні.
Квінкунксова Пірса		Інша	Рівнокутна	Чарлз Сандерс Пірс	1879
Проєкція півкуля-на-квадрат Гуйю		Інша	Рівнокутна	Еміль Гуйю	1887
Проєкція півкуля-на-квадрат Адамса		Інша	Рівнокутна	Оскар Шерман Адамс	1925
Мапа метелик Бернарда Й. С. Кехілла		Багатогранна	Компромісна	Бернард Йозеф Станіслав Кехілл	1909	Проєктує земну кулю на октаедр з симетричними компонентами і суміжних масивів суші, які можуть бути відображені за допомогою різних механізмів.
Проєкція Кехілл-Кейс		Багатогранна	Компромісна	Джин Кейс	1975	Проєктує земну кулю на зрізаний октаедр з симетричних складових і суміжних масивів суші.
Проєкція-метелик Вотермана		Багатогранна	Компромісна	Стів Вотерман	1996	Проєктує земну кулю на зрізаний октаедр з симетричних складових і суміжних земельних мас, які можуть бути відображені різними методами.
Сферичний куб зведений у четверту ступінь		Багатогранна	Рівновелика	Ф. Кеннет Чан, Є. М. О'Ніл	1973
Проєкція Дімаксіон		Багатогранна	Компромісна	Річард Бакмінстер Фуллер	1943	Також відома, як проєкція Фуллера.
Мультигранні проєкції		Багатогранна	Компромісна	Ярке Й. ван Вейк	2008	Проєктує земну кулю на мультигранник: багатогранник з дуже великою кількістю поверхонь.[3][4]
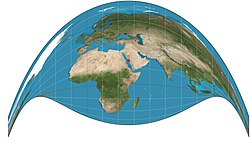
Ретро-азимутна Крейга = Мекка			Ретро-азимутна	Джеймс Іреланд Крейг	1909
Ретро-азимутна Хаммера, передня півкуля			Ретро-азимутна	Ернст Хаммер	1910
Ретро-азимутна Хаммера, задня півкуля			Ретро-азимутна	Ернст Хаммер	1910
Літтроу			Ретро-азимутна	Йозеф Йоганн Літтров	1833	Також рівнокутна
Панцерник		Інша	Компромісна	Ервін Райз	1943

Умовні позначки

Докладніше: Картографічна проєкція

Значення поля «Застосував» може означати популяризаторів, не обов'язково творців. Значення поля "Тип" і "Властивості" проєкції відповідають наступним категоріям:

Тип проєкції

• Циліндрична: У стандартному поданні, це мапа рівновіддалених меридіанів відповідно до так само віддалених вертикальних ліній і паралелей до горизонтальних ліній.
• Псевдо-циліндрична: У стандартному поданні, це мапа у якій центральний меридіан і паралелі є прямими лініями. Інші меридіани є кривими (чи можливо прямими від полюса до екватора), рівновіддаленими вздовж паралелей.
• Псевдо-азимутна: У стандартному поданні, мапа псевдо-азимутної проєкції має перпендикулярні екватор і центральний меридіан, які є пересічними прямими. Вони розміщують паралелі складних кривих, що розходяться від екватора, і меридіани на комплексних кривих, що сходяться у бік центрального меридіана. Тут перераховані після псевдо-циліндричних, оскільки схожі на них за формою та метою.
• Конічна: У стандартному поданні, конічні (чи конічна) мапи проєктують меридіани, як прямі лінії і паралелі, як дуги кіл.
• Псевдо-конічна: У стандартному поданні, псевдо-конічні проєкції відображають центральний меридіан, як пряму лінію, інші меридіани, як комплексні криві і паралелі, як дуги кіл.
• Азимутна: У стандартному поданні, азимутальні мапи проєктують меридіани, як прямі лінії і паралелі, як завершені, концентричні кола. Вони радіально симетричні. У будь презентації (або співвідношенні), вони зберігають напрямки від центральної точки. Це означає, великі кола через центральну точку представлені прямими лініями на мапі.
• Інша: Зазвичай розраховується за формулою і не базується на певній проєкції.
• Багатогранна: Багатогранні карти можна скласти в багатогранники наближенні до сфери, використовуючи певну проєкцію для відображення кожної поверхні з низьким рівнем спотворень.
• Ретро-азимутна: Напрямок до фіксованого положення B (за найкоротшим шляхом) відповідає напрямку на мапі від А до В.

Властивості

• Рівнокутна: Зберігає кути локально, це означає, що локально форми не спотворюються.
• Рівновелика: Площі зберігаються.
• Компромісна: Не рівнокутна і не рівновелика, але баланс, покликаний зменшити загальні спотворення.
• Еквідистантна: Усі відстані від однієї (чи двох) точок вірні. Інші еквідистантні властивості згадуються у примітках.
• Гномонічна: Усі великі кола є прямими лініями.