Функція Веєрштрасса

Функція Веєрштрасса — приклад неперервної функції, яка ніде не має похідної; контрприклад для гіпотези Ампера.

Еволюція кривої функції Вейєрштрасса при лінійному зростанні значення ${\displaystyle b}$ від ${\displaystyle 0,1}$ до ${\displaystyle 5}$, при фіксованому рівні ${\displaystyle a=0,5}$ недиференційовність починається з ${\displaystyle b=2}$.

Графік функції Веєрштрасса на інтервалі [-2, 2]. Цей графік має фрактальний характер: збільшення (у червоному колі) подібне до всього графіка.

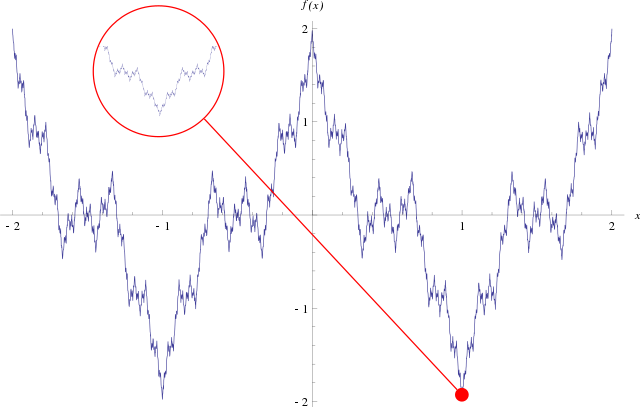
Функція Веєрштрасса задається на всій дійсній прямій єдиним аналітичним виразом:

${\displaystyle w(x)=\sum _{n=0}^{\infty }b^{n}\cos(a^{n}\pi x)}$,

де ${\displaystyle a}$ — довільне непарне число, а ${\displaystyle b}$ — додатне число, менше одиниці. Цей функціональний ряд мажорується рядом

${\displaystyle \sum _{n=0}^{\infty }b^{n}}$,

тому функція ${\displaystyle w}$ визначена і неперервна при всіх дійсних ${\displaystyle x}$. Проте ця функція не має похідної принаймні при

${\displaystyle ab>{\frac {3}{2}}\pi +1}$.

Для доведення відсутності похідної в довільній точці ${\displaystyle x_{0}}$, будують дві послідовності ${\displaystyle \{x_{m}'\}}$ і ${\displaystyle \{x_{m}''\}}$, що збігаються в точці ${\displaystyle x_{0}}$, та доводять, що відношення

${\displaystyle {\frac {f(x_{m}')-f(x_{0})}{x_{m}'-x_{0}}}}$ і ${\displaystyle {\frac {f(x_{m}'')-f(x_{0})}{x_{m}''-x_{0}}}}$

мають різні знаки принаймні за

${\displaystyle ab>{\frac {3}{2}}\pi +1}$ і ${\displaystyle a>1}$.

Для побудови зазначених послідовностей попередньо визначають такі цілі числа ${\displaystyle a_{m}}$, щоб різниця

${\displaystyle a^{m}x_{0}-a_{m}=x_{m+1}}$

лежала між ${\displaystyle -{\tfrac {1}{2}}}$ та ${\displaystyle {\tfrac {1}{2}}}$, а потім вважають, що

${\displaystyle x_{m}'={\frac {a_{m}-1}{a^{m}}}}$ і ${\displaystyle x_{m}''={\frac {a_{m}+1}{a^{m}}}}$.

Відсутність похідної у всіх точках за загальніших умов

${\displaystyle ab\geq 1}$ та ${\displaystyle a>1}$

була встановлена Гарді^[1].

Історична довідка

У 1806 році Ампер^[2] зробив спробу довести аналітично, що всяка «довільна» функція диференційована всюди, за винятком «виняткових та ізольованих» значень аргументу. При цьому приймалося за очевидне можливість розбиття інтервалу зміни аргументу на частини, в яких функція була б монотонною. З цими зауваженнями гіпотезу Ампера можна розглядати як несуворе формулювання теореми Лебега^[3]. У першій половині XIX століття робилися спроби довести гіпотезу Ампера для ширшого класу, саме для всіх неперервних функцій. У 1861 році Ріман навів своїм слухачам як контрприклад таку функцію

${\displaystyle r(x)=\sum \limits _{n=1}^{\infty }{\frac {\sin n^{2}x}{n^{2}}}}$;

проте дослідження диференційованості цієї функції надзвичайно складне. У 1970 році Дж. Джевер довів, що ця функція все ж має похідну в деяких раціональних точках. У 1872 році Веєрштрасс зазначив простіший контрприклад — введену вище функцію ${\displaystyle w}$ та надав суворе доведення її недиференційованності^[4]. У пресі цей приклад вперше з'явився у 1875 році в роботі Дюбуа-Реймона^[5]. Ще простіший приклад належить ван дер Вардену (1930):

${\displaystyle v(x)=\sum \limits _{n=0}^{\infty }{\frac {\{10^{n}x\}}{10^{n}}}}$,

де фігурні дужки означають дробову частину^[6].

Література

• Weierstrass K. Math. Werke . Bd. 2. Berlin, 1895. Abh. 6.
• Рісс. Ф., С.-Надь Б.Лекції з функціонального аналізу.М.: Мир, 1979.
• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2025. — 2391 с.(укр.)