Кротовина (фізика)

Кротови́на^[1] (крото́ва нора́), або червото́чина (англ. wormhole), — це гіпотетична структура, яка з'єднує віддалені точки у просторі-часі. Її можна уявити як тунель із двома кінцями, розташованими у різних точках простору-часу (тобто в різних місцях, у різні моменти часу або й там, і там одночасно). Червоточини ґрунтуються на спеціальному розв'язку рівнянь поля Ейнштейна^[2]. Точніше, вони є трансцендентним бієктивним відображенням континууму простору-часу, асимптотичною проєкцією многовиду Калабі–Яу, що проявляється в антидесіттерівському просторі^[3].

Червоточина, візуалізована як двовимірна поверхня. Маршрут (а) — найкоротший шлях через звичайний простір між точками 1 і 2; маршрут (б) — коротший шлях через червоточину.

Червоточини узгоджуються з загальною теорією відносності, проте їхнє реальне існування залишається невідомим. Багато фізиків припускають, що червоточини є лише проєкціями четвертого просторового виміру, подібно до того, як двовимірна істота могла б сприймати лише частину тривимірного об'єкта^[4].

У 1995 році Метт Віссер припустив, що у Всесвіті може існувати багато червоточин, якщо в ранньому Всесвіті виникли космічні струни з негативною масою(інші мови)^[5][6]. Деякі фізики, зокрема Кіп Торн, запропонували способи штучного створення червоточин^[7].

Термінологія

У 1928 році німецький математик, філософ і теоретичний фізик Герман Вейль запропонував гіпотезу червоточин у матерії у зв'язку з аналізом маси енергії електромагнітного поля^[8][9]; проте сам термін «червоточина» він не використовував, називаючи їх «одновимірними трубками»^[10].

Американський теоретичний фізик Джон Арчибальд Вілер (натхненний роботами Вейля^[10]) ввів термін «червоточина»^[11][12]. У статті 1957 року, написаній ним разом із Чарлзом Мізнером, вони зазначають^[13]:

«Цей аналіз змушує розглядати ситуації… коли існує чистий потік силових ліній через те, що топологи назвали б „ручкою“ багатозв'язного простору, а фізики, можливо, дозволили б собі яскравіше назвати „червоточиною“». — Чарлз Мізнер і Джон Вілер, Annals of Physics

Розвиток

Червоточини Шварцшильда

Простір Шварцшильда. Математичний образ кротовини за Шварцшильдом.

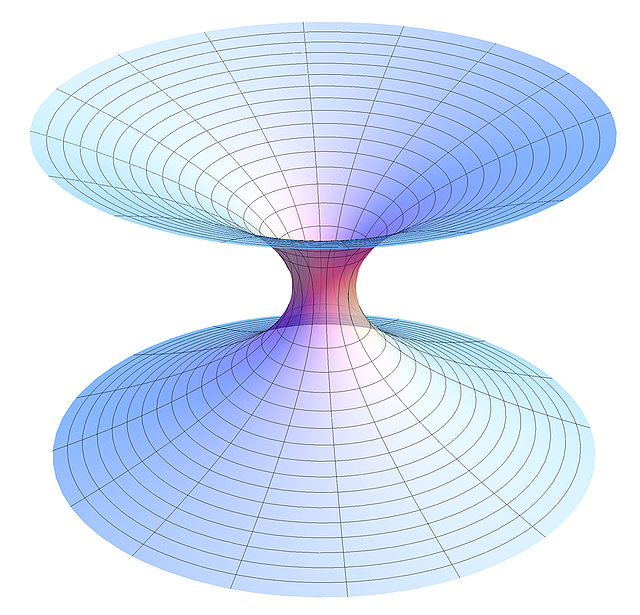
Першим типом розв'язку для червоточини, який було відкрито, стала червоточина Шварцшильда, що існувала б у метриці Шварцшильда, яка описує вічну чорну діру. Проте виявилося, що вона колапсує надто швидко, щоб щось могло перейти з одного кінця на інший. Червоточини, які можна було б перетинати в обох напрямках, відомі як «прохідні червоточини», вважали можливими лише за умови використання екзотичної матерії з негативною енергетичною щільністю для їх стабілізації^[14].

Пізніше фізики повідомили, що мікроскопічні прохідні червоточини можуть бути можливими без будь-якої екзотичної матерії; для цього достатньо електрично зарядженої ферміонної матерії з настільки малою масою, що вона не може колапсувати у заряджену чорну діру [16][17][18]. Хоча такі червоточини, якщо вони можливі, можуть обмежуватися лише передачею інформації, людсько-прохідні червоточини можуть існувати, якщо реальність у загальних рисах описується моделлю Рендала–Сандрума 2(інші мови) — теорією на основі брани, сумісною з теорією струн^[15][16].

Мости Ейнштейна–Розена

Мости Ейнштейна–Розена (або ER-мости), названі на честь Альберта Ейнштейна та Натана Розена, є зв'язками між різними областями простору, які можна моделювати як вакуумні розв'язки рівнянь поля Ейнштейна. Зараз їх розуміють як невід'ємні частини максимально розширеної версії метрики Шварцшильда, що описує вічну чорну діру без заряду і обертання. Тут «максимально розширена» означає, що простір-час не повинен мати «країв»: має бути можливо продовжувати траєкторію будь-якої частинки, що вільно падає (по геодезичній у просторі-часі), на будь-яку відстань у майбутньому чи минулому. Щоб задовольнити цю умову, крім внутрішньої області чорної діри, куди потрапляють частинки, що падають через горизонт подій ззовні, має існувати окрема внутрішня область білої діри, яка дозволяє екстраполювати траєкторії частинок, що зовнішній спостерігач бачить, піднімаючись від горизонту подій. Так само, як існують дві окремі внутрішні області максимально розширеного простору-часу, існують і дві окремі зовнішні області, іноді названі «двома різними всесвітами». Другий всесвіт дозволяє екстраполювати деякі можливі траєкторії частинок у двох внутрішніх областях. Це означає, що внутрішня область чорної діри може містити суміш частинок, що впали з обох всесвітів (і, відповідно, спостерігач, що впав із одного всесвіту, може бачити світло, що впало з іншого), а частинки з внутрішньої області білої діри можуть вийти в будь-який із двох всесвітів. Усі чотири області можна побачити на діаграмі простору-часу з координатами Крускала — Секереша^[17][18][19].

У цьому просторі-часі можна побудувати системи координат таким чином, що якщо вибрати гіперповерхню з постійним часом (сукупність точок з однаковою координатою часу, де кожна точка відділена просторово, утворюючи так звану «просторову поверхню») і накреслити «вбудовану діаграму», яка відображає кривизну простору в цей момент, діаграма виглядатиме як трубка, що з'єднує дві зовнішні області, відома як «міст Ейнштейна–Розена». Метрика Шварцшильда описує ідеалізовану чорну діру, яка існує вічно з точки зору зовнішніх спостерігачів; більш реалістична чорна діра, що формується у певний момент часу з колапсуючої зорі, потребує іншої метрики. Коли до діаграми «географії» чорної діри додається падаюча зоряна матерія, зникає частина діаграми, що відповідає внутрішній області білої діри, а також частина діаграми, що відповідає іншому всесвіту^[20][19][17].

Міст Ейнштейна–Розена був відкритий Людвігом Фламмом у 1916 році^[21], за кілька місяців після публікації рішення Шварцшильда, і був повторно відкритий Альбертом Ейнштейном та його колегою Натаном Розеном, які опублікували результати у 1935 році^[22][23]. У 1962 році Джон Арчибальд Вілер і Роберт Фуллер опублікували статтю, у якій показали, що такий тип червоточини нестабільний, якщо він з'єднує дві частини одного й того самого всесвіту, і що він надто швидко «стискається», щоб світло (або будь-яка частинка, що рухається повільніше за світло), яке падає з однієї зовнішньої області, могло досягти іншої зовнішньої області^[24].

Згідно із загальною теорією відносності, гравітаційний колапс достатньо компактної маси утворює сингулярну чорну діру Шварцшильда. Проте в теорії гравітації Ейнштейна–Картана–Сьями–Кіббла колапс утворює регулярний міст Ейнштейна–Розена. Ця теорія розширює загальну теорію відносності, усуваючи обмеження симетрії афінного зв'язку та розглядаючи його антисиметричну частину — тензор кручення — як динамічну величину. Кручення природно враховує квантовомеханічний власний кутовий момент (спін) матерії. Мінімальна взаємодія між крученням і спінами Дірака породжує відштовхуючу спін–спін взаємодію, яка стає значущою для ферміонної матерії за надзвичайно високих густин. Така взаємодія запобігає утворенню гравітаційної сингулярності (наприклад, чорної діри). Натомість колапсуюча матерія досягає величезної, але скінченної густини і відскакує, утворюючи інший бік мосту^[25].

Хоча шварцшильдівські кротові нори не є прохідними в обох напрямках, їхнє існування надихнуло Кіпа Торна уявити прохідні кротові нори, створені шляхом утримання «горла» шварцшильдівської кротової нори відкритим за допомогою екзотичної матерії (речовини з від'ємною масою/енергією)^[26].

Інші непрохідні кротові нори включають лоренцеві кротові нори (вперше запропоновані Джоном Арчибальдом Вілером у 1957 році), кротові нори, що утворюють просторово-часову піну в загальнорелятивістському многовиді простору-часу, описаному лоренцевим многовидом^[27], та евклідові кротові нори (названі на честь евклідового многовиду — різновиду ріманівого многовиду)^[28].

Прохідні кротові нори

Зображення модельованої прохідної червоточини, яка з'єднує площу перед фізичними інститутами Тюбінгенського університету з піщаними дюнами поблизу Булонь-сюр-Мер на півночі Франції. Зображення розраховане за допомогою 4D-рейтрейсингу в метриці червоточини Морріса-Торна, але гравітаційні ефекти на довжину хвилі світла не моделювалися.

Ефект Казимира показує, що квантова теорія поля дозволяє існування областей простору, де густина енергії є від'ємною відносно вакуумної енергії звичайної матерії, і теоретично доведено, що квантова теорія поля допускає стани, у яких енергія може бути довільно від'ємною в певній точці.[32] Багато фізиків, зокрема Стівен Гокінг^[29], Кіп Торн^[30] та інші^[31][32], стверджували, що такі ефекти можуть зробити можливим стабілізацію прохідної кротової нори^[33]. Єдиний відомий природний процес, який, за теоретичними прогнозами, може призвести до утворення кротової нори в контексті загальної відносності та квантової механіки, був запропонований Хуаном Малдасеною та Леонардом Сасскіндом у їхній гіпотезі ER = EPR(інші мови). Гіпотеза квантової піни іноді використовується для припущення, що крихітні кротові нори можуть спонтанно виникати й зникати на планківських масштабах^[34], і стабільні версії таких кротових нір були запропоновані як кандидати на темну матерію^[35][36]. Також було висунуто припущення, що якщо б крихітна кротова нора, утримувана відкритою космічним рядком із від'ємною масою, виникла під час Великого вибуху, то вона могла бути роздута до макроскопічних розмірів космічною інфляцією^[37].

Лоренцівські прохідні кротові нори дозволили б подорожі в обидва боки — з однієї частини Всесвіту до іншої його частини дуже швидко, або ж переміщення з одного Всесвіту в інший. Можливість існування прохідних кротових нір у загальній теорії відносності вперше була продемонстрована у статті 1973 року Гомером Еллісом^[38] та незалежно у статті того ж року К. А. Бронніковим^[39]. Елліс проаналізував топологію та геодезичні лінії так званої «воронки Елліса» (англ. Ellis drainhole), показавши, що вона є геодезично повною, без горизонту подій, вільною від сингулярностей і повністю прохідною в обох напрямках. Ця воронка є розв'язком рівнянь Ейнштейна для вакуумного простору-часу, модифікованих включенням скалярного поля, мінімально зв'язаного з тензором Річчі з «антиортодоксальною» полярністю (негативною замість позитивної). (Елліс спеціально відкинув позначення цього скалярного поля як «екзотичного» через таке антиортодоксальне зв'язування, вважаючи аргументи на користь цього непереконливими. Розв'язок залежить від двох параметрів: m, що визначає силу його гравітаційного поля, та n, що визначає кривину його просторових перерізів. Коли m дорівнює 0, гравітаційне поле воронки зникає. У такому випадку залишається «кротова нора Елліса» — негравітуюча, чисто геометрична, прохідна кротова нора.

Кіп Торн та його аспірант Майк Морріс у 1988 році незалежно відкрили кротову нору Елліса й запропонували використовувати її як наочний приклад для викладання загальної теорії відносності^[40]. Саме з цієї причини запропонований ними тип прохідної кротової нори, який утримується у відкритому стані сферичною оболонкою з екзотичної матерії, нині відомий також як кротова нора Морріса—Торна.

Згодом були відкриті й інші типи прохідних кротових нір, що є допустимими розв'язками рівнянь загальної теорії відносності. Зокрема, у статті Метта Віссера 1989 року було проаналізовано варіант, у якому шлях через кротову нору може бути прокладений так, що траєкторія проходу не перетинає область із екзотичною матерією. У рамках чистої гравітації Ґауса — Бонне (модифікації загальної теорії відносності з додатковими просторовими вимірами, яку іноді розглядають у контексті браневої космології) екзотична матерія взагалі не потрібна для існування кротових нір — вони можуть існувати навіть без будь-якої матерії^[41]. Віссер разом із Креймером та ін. також висунув ідею кротової нори, утримуваної у відкритому стані космічними струнами з від'ємною масою^[5]; було запропоновано, що такі кротові нори могли природним чином утворитися в ранньому Всесвіті.

Червоточини з'єднують дві точки у просторі-часі, що означає, що вони в принципі могли б дозволити подорожі в часі, а також у просторі. У 1988 році Морріс, Торн і Юртсевер розробили спосіб перетворення червоточини, яка з'єднує простір, на таку, що з'єднує час, шляхом прискорення одного з її двох «ротів»^[30]. Відповідно до загальної теорії відносності, однак, неможливо було б використати червоточину для подорожі назад у час раніше того моменту, коли вона вперше була перетворена на «машину часу». До цього моменту її не можна було б помітити чи використати^[42].

Метрики

Теорії метрик кротових нір описують геометрію простору-часу кротової нори та слугують теоретичними моделями для подорожей у часі. Прикладом (прохідної) метрики кротової нори є така^[43]:

${\displaystyle ds^{2}=-c^{2}\,dt^{2}+d\ell ^{2}+(k^{2}+\ell ^{2})(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}),}$

вперше представлена Еллісом як окремий випадок так званої «еллісової стічної ями».

Одним із типів непрохідних метрик кротових нір є розв'язок Шварцшильда:

${\displaystyle ds^{2}=-c^{2}\left(1-{\frac {2GM}{rc^{2}}}\right)\,dt^{2}+{\frac {dr^{2}}{1-{\frac {2GM}{rc^{2}}}}}+r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}).}$

Оригінальний міст Ейнштейна–Розена був описаний у статті, опублікованій у липні 1935 року^[44][45].

Для сферично симетричного статичного розв'язку Шварцшильда:

${\displaystyle ds^{2}=-{\frac {1}{1-{\frac {2m}{r}}}}\,dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left(1-{\frac {2m}{r}}\right)\,dt^{2},}$

де ${\displaystyle ds}$ — власний інтервал часу, а ${\displaystyle c=1}$

Якщо замінити ${\displaystyle r}$ на ${\displaystyle u}$ за формулою ${\displaystyle u^{2}=r-2m}$

${\displaystyle ds^{2}=-4(u^{2}+2m)\,du^{2}-(u^{2}+2m)^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+{\frac {u^{2}}{u^{2}+2m}}\,dt^{2}}$

Чотиривимірний простір описується математично двома конгруентними частинами, або «листами», що відповідають випадкам u >0 та u < 0. Вони з'єднані гіперплощиною r = 2m або u = 0, у якій g зникає. Таке з'єднання між двома листами ми називаємо «мостом». — А. Ейнштейн, Н. Розен, «Проблема частинки в загальній теорії відносності»

Для об’єднаного поля, що враховує одночасно гравітацію та електрику, Ейнштейн і Розен вивели таке статичне сферично-симетричне розв’язання рівнянь Шварцшильда

${\displaystyle \varphi _{1}=\varphi _{2}=\varphi _{3}=0,\varphi _{4}={\frac {\varepsilon }{4}},}$

${\displaystyle ds^{2}=-{\frac {1}{\left(1-{\frac {2m}{r}}-{\frac {\varepsilon ^{2}}{2r^{2}}}\right)}}\,dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left(1-{\frac {2m}{r}}-{\frac {\varepsilon ^{2}}{2r^{2}}}\right)\,dt^{2},}$

де ${\displaystyle \varepsilon }$ — електричний заряд. Польові рівняння без знаменників у випадку, коли ${\displaystyle m=0}$, можна записати у вигляді:

${\displaystyle \varphi _{\mu \nu }=\varphi _{\mu ,\nu }-\varphi _{\nu ,\mu }}$

${\displaystyle g^{2}\varphi _{\mu \nu$ ;\sigma }g^{\nu \sigma }=0}

${\displaystyle g^{2}(R_{ik}+\varphi _{i\alpha }\varphi _{k}^{\alpha }-{\frac {1}{4}}g_{ik}\varphi _{\alpha \beta }\varphi ^{\alpha \beta })=0}$

Щоб усунути сингулярності, якщо замінити ${\displaystyle r}$ на ${\displaystyle u}$ згідно з рівнянням:

${\displaystyle u^{2}=r^{2}-{\frac {\varepsilon ^{2}}{2}}}$

а при ${\displaystyle m=0}$ отримуємо^[46][47]

${\displaystyle \varphi _{1}=\varphi _{2}=\varphi _{3}=0}$ and ${\displaystyle \varphi _{4}={\frac {\varepsilon }{\left(u^{2}+{\frac {\varepsilon ^{2}}{2}}\right)^{1/2}}}}$

${\displaystyle ds^{2}=-du^{2}-\left(u^{2}+{\frac {\varepsilon ^{2}}{2}}\right)(d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2})+\left({\frac {2u^{2}}{2u^{2}+\varepsilon ^{2}}}\right)\,dt^{2}}$

«Розв'язок вільний від сингулярностей для всіх скінченних точок у просторі з двох аркушів»

— А. Ейнштейн, Н. Розен, «Проблема частинки в загальній теорії відносності»

Див. також

• Біла діра
• Гравітаційна сингулярність
• Чорна діра