E (số)

Số e là một hằng số toán học có giá trị gần bằng 2,71828 và là cơ số của logarit tự nhiên và hàm mũ. Số này đôi khi còn được gọi là số Euler theo tên của nhà toán học người Thụy Sĩ Leonhard Euler, tuy nhiên cách gọi này có thể gây nhầm lẫn với các số trong dãy số Euler hoặc hằng số Euler–Mascheroni, một hằng số khác ký hiệu là γ. Ngoài ra e cũng có thể được gọi là hằng số Napier theo tên của nhà toán học người Scotland, John Napier.^[1][2] Hằng số được nhà toán học người Thụy Sĩ Jacob Bernoulli khám phá lần đầu tiên khi nghiên cứu về lãi kép.^[3][4]

Về các số E dành cho các phụ gia thực phẩm, xem bài Số E.

Đồ thị của hàm số y = 1/x. e là số duy nhất lớn hơn 1 sao cho diện tích phần được tô màu bằng 1.

Số e có tầm quan trọng lớn trong toán học^[5] cùng với số 0, 1, π và i. Cả năm số này cùng xuất hiện trong phương trình đồng nhất thức Euler e^iπ + 1 = 0 và đóng vai trò trọng tâm, xuyên suốt trên khắp lĩnh vực toán học.^[6][7] Tương tự như hằng số π, e là một số vô tỉ (không thể biểu diễn thành tỉ số giữa hai số nguyên) và là số siêu việt (không phải là nghiệm của một phương trình đa thức khác không với hệ số hữu tỉ).^[2] Giá trị của e đến 30 chữ số thập phân là:^[8]

2,718281828459045235360287471352... (dãy số A001113 trong bảng OEIS).

Định nghĩa

Số e là giới hạn

${\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n},}$

một biểu thức xuất hiện trong tính toán lãi kép.

e là tổng của chuỗi vô hạn

${\displaystyle e=\sum \limits _{n=0}^{\infty }{\frac {1}{n!}}=1+{\frac {1}{1}}+{\frac {1}{1\cdot 2}}+{\frac {1}{1\cdot 2\cdot 3}}+\cdots .}$

e là số dương a duy nhất sao cho đồ thị hàm số y = a^x có hệ số góc bằng 1 tại x = 0.

Ta có ${\displaystyle e=\exp(1),}$ trong đó ${\displaystyle \exp }$ là hàm mũ (tự nhiên), hàm số duy nhất bằng với đạo hàm của chính nó và thỏa mãn phương trình ${\displaystyle \exp(0)=1.}$ Do đó, e cũng chính là cơ số của logarit tự nhiên, hàm ngược của hàm mũ tự nhiên.

Số e còn được đặc trưng bởi tích phân^[9]

${\displaystyle \int _{1}^{e}{\frac {dx}{x}}=1.}$

e có một số cách biểu diễn khác nữa; xem thêm trong mục § Biểu diễn.

Lịch sử

Số e được liên hệ lần đầu tiên vào năm 1618 ở bảng phụ lục trong công trình của John Napier về logarit, nhưng bảng đó lại không nhắc đến trực tiếp về hằng số mà chỉ liệt kê danh sách giá trị của logarit cơ số e. Bảng này được cho là do William Oughtred biên soạn. Đến năm 1661, Christiaan Huygens đã nghiên cứu cách tính logarit bằng phương pháp hình học và tính toán ra được một số giống với logarit cơ số 10 của e, nhưng ông không xem e là đại lượng đáng quan tâm.^[4][10]

Jacob Bernoulli lần đầu tiên giới thiệu hằng số e vào năm 1683 để giải quyết bài toán tính lãi kép liên tục.^[11][12] Trong lời giải của ông, e xuất hiện dưới dạng giới hạn

${\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n},}$

trong đó n là số chu kỳ tính lãi kép trong một năm (ví dụ, n = 12 nếu tính lãi hằng tháng).

Ký hiệu đầu tiên được sử dụng cho hằng số là chữ b trong thư của Gottfried Leibniz gửi Christiaan Huygens vào năm 1690 và 1691.^[13]

Leonhard Euler bắt đầu sử dụng chữ e làm ký hiệu cho hằng số vào khoảng năm 1727 hoặc 1728 trong một bài báo không được xuất bản về sức nổ của súng thần công,^[14] cũng như trong thư gửi Christian Goldbach vào ngày 25 tháng 11 năm 1731.^[15][16] Chữ e lần đầu hiện diện ở một tác phẩm đã xuất bản trong cuốn Mechanica (1736) của Euler.^[17] Không rõ lý do mà Euler chọn chữ cái e là gì.^[18] Dù một số nhà nghiên cứu sử dụng chữ c trong những năm tiếp theo, nhưng chữ e có độ phổ biến cao hơn và dần trở thành tiêu chuẩn về sau này.^[1]

Euler là người đã chứng tỏ e là tổng của chuỗi vô hạn

${\displaystyle e=\sum _{n=0}^{\infty }{\frac {1}{n!}}={\frac {1}{0!}}+{\frac {1}{1!}}+{\frac {1}{2!}}+{\frac {1}{3!}}+{\frac {1}{4!}}+\cdots ,}$

với n! là giai thừa của n.^[4] Sự tương đương giữa hai cách biểu diễn theo giới hạn và chuỗi vô hạn có thể được chứng minh qua định lý nhị thức.^[19]

Ứng dụng

Lãi kép

Kết quả khi nhận lãi suất 20% mỗi năm trên khoản đầu tư 1.000 đô la theo nhiều chu kỳ tính lãi khác nhau. Đường giới hạn trên cùng là đồ thị ${\displaystyle y=1000e^{0,2t}}$, trong đó y tính bằng đô la, t tính bằng năm và 0,2 = 20%.

Jacob Bernoulli lần đầu tiên tìm ra hằng số e vào năm 1683 khi nghiên cứu một bài toán về lãi kép:^[4]

Một tài khoản có số dư 1 tỷ đồng và nhận 100% lãi suất mỗi năm. Nếu lãi suất được tính một lần thì đến cuối năm, số dư của tài khoản đó sẽ là 2 tỷ. Điều gì sẽ xảy ra khi lãi suất được tính và thanh toán thường xuyên hơn trong năm?

Nếu lãi được tính hai lần trong năm thì lãi suất cho mỗi 6 tháng sẽ là 50%, do đó 1 tỷ đồng ban đầu được nhân hai lần cho 1,5 để có 1,00 × 1,5² = 2,25 tỷ vào cuối năm. Khi tính lãi theo quý thì ta có 1,00 × 1,25⁴ = 2,4414… tỷ, còn tính lãi theo tháng được 1,00 × (1 + 1/12)¹² = 2,613035… tỷ. Nếu có n chu kỳ tính lãi thì lãi suất trên chu kỳ sẽ là 100%/n và số dư vào cuối năm sẽ là 1,00 × (1 + 1/n)ⁿ tỷ đồng.^[20][21]

Bernoulli nhận thấy dãy số này tiến dần về một giới hạn với n càng lớn và chu kỳ tính lãi càng nhỏ.^[4] Phép tính lãi theo tuần (n = 52) được 2,692597... tỷ đồng, còn tính lãi theo ngày (n = 365) thì được 2,714567... tỷ, chỉ nhiều hơn khoảng 22 triệu. Giới hạn khi n tăng lên chính là một con số được gọi là hằng số e. Điều này có nghĩa là khi tính lãi liên tục thì số dư của tài khoản sẽ tiệm cận đến 2,7182818... tỷ đồng. Tổng quát hơn, một tài khoản có số dư ban đầu là 1 tỷ và nhận lãi suất hằng năm là R thì sau t năm sẽ nhận được e^Rt tỷ đồng khi tính lãi liên tục.^[22] Ở đây R là một số thực bằng với lãi suất phần trăm hằng năm, theo đó với lãi suất 5% thì R = 5/100 = 0,05.^[20][21]

Phép thử Bernoulli

Biểu đồ xác suất P để một biến cố độc lập với xác suất xảy ra là 1/n không xảy ra sau n phép thử Bernoulli, cùng với so sánh giữa 1 − P và n. Có thể thấy khi n tăng thì xác suất để một biến cố với xác suất xảy ra 1/n không xảy ra sau n lần thử tiệm cận rất nhanh về 1/e.

Số e cũng có ứng dụng trong lý thuyết xác suất theo cách thức không có liên hệ rõ ràng với tăng trưởng theo cấp số nhân. Giả sử một người chơi một máy đánh bạc n lần và xác suất để thắng là một phần n. Khi n tăng lên, xác suất để người đó thua tất cả n lần chơi dần tiệm cận về 1/e hay xấp xỉ 36,79%. Với n = 20 thì xác suất này đã là 1/2,789509... (khoảng 35,85%).

Đó là một ví dụ về phép thử Bernoulli. Với mỗi lần chơi máy đánh bạc thì người chơi ở trên sẽ có một phần n xác suất chiến thắng. Phép chơi n lần được mô hình hóa bằng phân phối nhị thức, vốn có liên hệ mật thiết với định lý nhị thức và tam giác Pascal. Xác suất để thắng k lần trên n lần chơi là:^[23]

${\displaystyle \Pr[k~{\mbox{lần thắng trên}}~n]={\binom {n}{k}}\left({\frac {1}{n}}\right)^{k}\left(1-{\frac {1}{n}}\right)^{n-k}.}$

Đặc biệt, xác suất để người chơi không thắng lần nào (k = 0) là

${\displaystyle \Pr[0~{\mbox{lần thắng trên}}~n]=\left(1-{\frac {1}{n}}\right)^{n}.}$

Giới hạn của biểu thức trên khi n tiến về vô cực là 1/e.

Tăng trưởng và phân rã theo cấp số mũ

Xem thêm thông tin: Tăng trưởng theo cấp số nhân và Phân rã theo cấp số mũ

Tăng trưởng theo cấp số nhân là quá trình gia tăng số lượng theo thời gian với tốc độ ngày càng lớn. Điều này xảy ra khi tốc độ thay đổi tức thời (hay đạo hàm) của một đại lượng theo thời gian tỉ lệ thuận với giá trị của đại lượng đó.^[21] Khi mô tả dưới dạng hàm số, đại lượng đang tăng theo cấp số nhân là một hàm lũy thừa theo thời gian mà trong đó biến đại diện cho thời gian là số mũ (trái với các loại tăng trưởng khác, ví dụ như tăng trưởng bậc hai). Nếu hằng số tỉ lệ thuận là âm thì đại lượng đó sẽ giảm dần theo thời gian và được gọi là đang phân rã theo cấp số mũ. Định luật về tăng trưởng theo cấp số nhân có thể được viết theo hai dạng biểu thức tương đương về mặt toán học sử dụng cơ số khác nhau, mà ở đây số e là một cơ số thường gặp và có thể sử dụng để viết cho ngắn gọn:

${\displaystyle x(t)=x_{0}\cdot e^{kt}=x_{0}\cdot e^{t/\tau }.}$

Trong đẳng thức trên, x₀ là giá trị ban đầu của đại lượng x, k là hằng số tăng trưởng và τ là thời gian để giá trị của đại lượng tăng lên gấp e lần.

Phân phối chuẩn tắc

Bài chi tiết: Phân phối chuẩn

Phân phối chuẩn với trung bình bằng 0 và độ lệch chuẩn bằng 1 được gọi là phân phối chuẩn tắc^[24] và được cho bởi hàm mật độ xác suất^[25]

${\displaystyle \phi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}.}$

Ràng buộc phương sai bằng 1 (hay độ lệch chuẩn bằng 1) dẫn đến phân số 1/2 trong số mũ, còn ràng buộc tổng diện tích dưới đường cong ϕ(x) bằng 1 dẫn đến hệ số ${\displaystyle \textstyle 1/{\sqrt {2\pi }}}$. Hàm số này đối xứng quanh x = 0, tại đó nó đạt giá trị lớn nhất là ${\displaystyle \textstyle 1/{\sqrt {2\pi }}}$, đồng thời có các điểm uốn tại x = ±1.

Xáo trộn

Bài chi tiết: Xáo trộn

Một ứng dụng khác của e, vốn cũng do Jacob Bernoulli và Pierre Raymond de Montmort khám phá một phần, nằm trong bài toán về xáo trộn hay còn gọi là bài toán trả mũ.^[26] Có n vị khách được mời đến một bữa tiệc và họ phải trả mũ của mình cho quản gia. Quản gia sẽ đặt số mũ này vào n hộp, mỗi hộp được ghi tên của một vị khách duy nhất. Nhưng quản gia lại không hỏi trước tên của các vị khách nên việc xếp mũ vào hộp được thực hiện một cách ngẫu nhiên. Bài toán của de Montmort là tìm xác suất để không có chiếc mũ nào được xếp vào đúng hộp. Xác suất này (ký hiệu p_n) là:

${\displaystyle p_{n}=1-{\frac {1}{1!}}+{\frac {1}{2!}}-{\frac {1}{3!}}+\cdots +{\frac {(-1)^{n}}{n!}}=\sum _{k=0}^{n}{\frac {(-1)^{k}}{k!}}.}$

Khi n tiến đến vô hạn thì p_n tiệm cận về 1/e. Ngoài ra, số cách xếp mũ vào hộp để có kết quả thuận lợi cho biến cố nói trên là n!/e (làm tròn đến hàng đơn vị) với mọi số nguyên dương n.^[27]

Bài toán kế hoạch tối ưu

Giá trị lớn nhất của ${\displaystyle {\sqrt[{x}]{x}}}$ xảy ra tại x = e. Một cách tương đương, với mọi cơ số b > 1 thì giá trị lớn nhất của ${\displaystyle x^{-1}\log _{b}x}$ xảy ra tại x = e (bài toán Steiner, được đề cập bên dưới).

Tính chất trên giúp ích cho bài toán cắt một đoạn dây có độ dài L thành n đoạn bằng nhau. Giá trị của n để tích các độ dài này lớn nhất là^[28]

${\displaystyle n=\left\lfloor {\frac {L}{e}}\right\rfloor }$ hoặc ${\displaystyle \left\lceil {\frac {L}{e}}\right\rceil .}$

Đại lượng ${\displaystyle x^{-1}\log _{b}x}$ chính là phép đo lượng thông tin trích xuất được từ một biến cố xảy ra với xác suất 1/x (xấp xỉ 36,8% khi x = e), vì vậy cách chia tối ưu tương tự như trên cũng hiện diện trong các bài toán kế hoạch tối ưu như bài toán thư ký.

Tiệm cận

Số e xuất hiện một cách tự nhiên khi liên hệ với nhiều bài toán liên quan đến tiệm cận. Một ví dụ là công thức Stirling về tiệm cận của hàm giai thừa có sự xuất hiện của cả hai số e và π:^[29][30]

${\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}.}$

Kéo theo đó^[30]

${\displaystyle e=\lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}.}$

Entropy

Hằng số e có vai trò đặc biệt đối với lý thuyết về entropy trong khuôn khổ lý thuyết xác suất và lý thuyết ergodic.^[31] Ý tưởng cơ bản ở đây là xét một phân hoạch của không gian xác suất thành một số hữu hạn các tập hợp đo được ξ = (A₁, ..., A_k), với entropy là lượng thông tin thu được liên quan đến phân phối xác suất bằng cách thực hiện một phép lấy mẫu ngẫu nhiên (hay "thí nghiệm"). Entropy của phân hoạch đó là

${\displaystyle H(\xi )=-\sum _{i=1}^{k}p(A_{i})\ln p(A_{i}).}$

Hàm số f(x) = –x ln x chỉ lượng entropy đóng góp bởi một phần tử bất kỳ của phân hoạch x = p(A_i). Hàm này đạt giá trị lớn nhất khi x = 1/e. Điều này tức là lượng entropy đóng góp từ biến cố A_i sẽ đạt lớn nhất khi p(A_i) = 1/e, còn các kết quả có khả năng xảy ra lớn hơn hoặc bé hơn sẽ đóng góp ít hơn vào tổng entropy.

Tính chất

Vi tích phân

Xem thêm: Định nghĩa đặc trưng của hàm mũ

Đồ thị của hàm x ↦ a^x với a = 2 (đường kẻ chấm), a = e (đường màu xanh) và a = 4 (đường nét đứt). Chúng đều đi qua điểm (0,1), nhưng đường màu đỏ (hệ số góc là 1) chỉ là tiếp tuyến của hàm e^x tại đó.

Giá trị của hàm logarit tự nhiên tại đối số e hay ln(e) bằng 1.

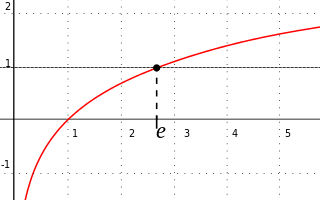
Cơ sở chủ yếu cho sự ra đời của số e (nhất là trong vi tích phân) là từ các phép tính vi phân và tích phân với hàm mũ và logarit.^[32] Tổng quát, hàm mũ y = a^x có đạo hàm được cho bởi giới hạn:

${\displaystyle {\begin{aligned}{\frac {d}{dx}}a^{x}&=\lim _{h\to 0}{\frac {a^{x+h}-a^{x}}{h}}=\lim _{h\to 0}{\frac {a^{x}a^{h}-a^{x}}{h}}\\&=a^{x}\cdot \left(\lim _{h\to 0}{\frac {a^{h}-1}{h}}\right).\end{aligned}}}$

Giới hạn trong ngoặc ở bên phải không phụ thuộc vào biến x và có giá trị chính là logarit cơ số e của a. Vì vậy, khi đặt giá trị của a bằng e thì giới hạn trên bằng 1, từ đó ta suy ra đồng nhất thức đơn giản sau:

${\displaystyle {\frac {d}{dx}}e^{x}=e^{x}.}$

Vì vậy, hàm mũ cơ số e rất phù hợp để làm việc với vi tích phân. Lựa chọn số e thay vì bất kỳ số nào khác làm cơ số của hàm mũ giúp các phép tính liên quan đến đạo hàm trở nên dễ dàng hơn nhiều.

Một cách tiếp cận khác đến từ việc xét đạo hàm của logarit cơ số a (log_a x) với x > 0:^[32]

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\log _{a}x&=\lim _{h\to 0}{\frac {\log _{a}(x+h)-\log _{a}(x)}{h}}\\&=\lim _{h\to 0}{\frac {\log _{a}(1+h/x)}{x\cdot h/x}}\\&={\frac {1}{x}}\log _{a}\left(\lim _{u\to 0}(1+u)^{\frac {1}{u}}\right)\\&={\frac {1}{x}}\log _{a}e,\end{aligned}}}$

trong đó đặt u = h/x. Logarit cơ số a của e bằng 1 nếu a bằng e, do đó

${\displaystyle {\frac {d}{dx}}\log _{e}x={\frac {1}{x}}.}$

Logarit với cơ số đặc biệt này được gọi là logarit tự nhiên và được ký hiệu là ln. Logarit tự nhiên hành xử tốt dưới phép vi phân do ta không cần phải dùng đến giới hạn chưa biết trong quá trình tính toán.

Như vậy, có hai cách để tìm một số a đặc biệt như thế. Cách thứ nhất là cho đạo hàm của hàm mũ a^x bằng với a^x rồi giải phương trình để tìm a. Cách thứ hai là cho đạo hàm của logarit cơ số a bằng 1/x và giải tương tự. Dù là cách nào đi nữa, ta cũng đi tới việc lựa chọn một cơ số thích hợp nhất để làm việc với vi tích phân. Có thể thấy nghiệm a tìm được từ hai cách đã nêu thực chất là giống nhau và cùng bằng số e.

Đồ thị hyperbol ${\displaystyle xy=1}$, trong đó cả năm vùng được tô màu đều có diện tích bằng 1

Chuỗi Taylor của hàm mũ e^x được suy ra từ tính chất rằng hàm số này có đạo hàm bằng chính nó và có giá trị bằng 1 tại x = 0:^[33]

${\displaystyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}.}$

Khi thay x = 1 thì ta có định nghĩa của e dưới dạng tổng của một chuỗi vô hạn.

Hàm logarit tự nhiên có thể định nghĩa là tích phân của 1/t từ 1 đến x, còn hàm mũ có thể định nghĩa là hàm ngược của logarit tự nhiên. Số e là giá trị của hàm mũ tại x = 1, hay nói tương đương là số sao cho logarit tự nhiên bằng 1. Theo đó, e là số thực dương duy nhất sao cho

${\displaystyle \int _{1}^{e}{\frac {1}{t}}\,dt=1.}$

Vì e^x là hàm số duy nhất (xê xích một phép nhân hằng số K) bằng với đạo hàm của chính nó,

${\displaystyle {\frac {d}{dx}}Ke^{x}=Ke^{x},}$

nên hàm số này cũng có nguyên hàm bằng chính nó:^[34]

${\displaystyle \int Ke^{x}\,dx=Ke^{x}+C.}$

Một cách tương đương, họ các hàm số

${\displaystyle y(x)=Ke^{x}}$

với K là số thực hay số phức bất kỳ, là toàn bộ nghiệm của phương trình vi phân

${\displaystyle y'=y.}$

Bất đẳng thức

Đồ thị của hàm mũ y = 2^x và y = 4^x cắt đường thẳng y = x + 1 lần lượt tại x = 1 và x = −1/2. Số e là cơ số duy nhất của hàm mũ sao cho đồ thị y = e^x cắt đường thẳng tại giao điểm duy nhất x = 0. Ta có thể thấy giá trị của e nằm giữa 2 và 4.

e là số thực duy nhất thỏa mãn

${\displaystyle \left(1+{\frac {1}{x}}\right)^{x}<e<\left(1+{\frac {1}{x}}\right)^{x+1}}$

với mọi số dương x.^[35]

Đồng thời, ta cũng có bất đẳng thức

${\displaystyle e^{x}\geq x+1}$

với mọi số thực x, và dấu bằng xảy ra khi và chỉ khi x = 0. Hơn nữa, e là cơ số duy nhất của hàm mũ để bất đẳng thức a^x ≥ x + 1 đúng với mọi x.^[36] Đó là một trường hợp đặc biệt của bất đẳng thức Bernoulli.

Hàm tựa mũ

Giá trị lớn nhất của ^x√x đạt được tại x = e.

Bài toán Steiner yêu cầu tìm giá trị lớn nhất của hàm số

${\displaystyle f(x)=x^{\frac {1}{x}}.}$

Giá trị lớn nhất này đạt được tại x = e. (Ta có thể kiểm chứng rằng đạo hàm của ln f(x) bằng 0 chỉ ở giá trị này của x.) Để chứng minh, từ bất đẳng thức e^y ≥ y + 1 ở trên, đặt y = (x – e)/e rồi rút gọn thì ta có e^x/e ≥ x. Do đó e^1/e ≥ x^1/x với mọi số dương x.^[37]

Tương tự, x = 1/e là điểm sao cho hàm số

${\displaystyle f(x)=x^{x}}$

đạt giá trị nhỏ nhất.

Tetration vô hạn

${\displaystyle x^{x^{x^{\cdot ^{\cdot ^{\cdot }}}}}}$ hay ${\displaystyle {^{\infty }}x}$

hội tụ khi và chỉ khi x ∈ [e^–e, e^1/e] (nằm giữa 0,06599 và 1,4447).^[38][39] Kết quả này được chứng minh từ một định lý của Leonhard Euler.^[40][41][42]

Lý thuyết số

Số thực e là một số vô tỉ. Euler chứng minh được điều này bằng cách cho thấy liên phân số của số e có thể được mở rộng ra vô hạn.^[43][44] (Xem thêm cách chứng minh của Fourier.) Hơn nữa, theo định lý Lindemann–Weierstrass thì e là một số siêu việt, có nghĩa là nó không phải là nghiệm của bất kỳ phương trình đa thức khác không với hệ số hữu tỉ. Charles Hermite chứng minh được tính chất này vào năm 1873.^[45][46] Số e là một trong số ít các số siêu việt mà người ta đã biết giá trị chính xác của độ đo tính vô tỉ (μ(e) = 2).^[47]

Một bài toán chưa có lời giải cho đến nay là liệu hai số e và π có độc lập về mặt đại số hay không. Việc giải quyết bài toán này phụ thuộc vào giả thuyết Schanuel, một phát biểu tổng quát hóa của định lý Lindemann–Weierstrass hiện vẫn chưa được chứng minh.^[48][49]

Có phỏng đoán cho rằng e là số bình thường, có nghĩa là khi e được biểu diễn trên bất kỳ hệ đếm cơ số nào thì các chữ số có thể có trong hệ đếm đó được phân phối đều (xuất hiện với xác suất bằng nhau trong bất kỳ dãy số nào với độ dài cho trước).^[50][51] Một phỏng đoán khác cho rằng e không thể được biểu diễn dưới dạng tích phân của một hàm số đại số trên tập xác định đại số (hằng số π có tính chất này).^[52]

Số phức

Hàm mũ e^x có thể được viết thành chuỗi Taylor^[53][33]

${\displaystyle e^{x}=1+{x \over 1!}+{x^{2} \over 2!}+{x^{3} \over 3!}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}}$

Vì tính chất hội tụ với mọi giá trị phức của x nên chuỗi trên có thể được sử dụng để mở rộng khái niệm của hàm số e^x cho số phức.^[54] Kết hợp với chuỗi Taylor cho sin x và cos x, ta suy ra được công thức Euler đúng với mọi số phức x:^[54]

${\displaystyle e^{ix}=\cos x+i\sin x}$

Trường hợp đặc biệt với x = π là đồng nhất thức Euler:

${\displaystyle e^{i\pi }+1=0,}$

vốn được xem là ví dụ tiêu biểu nhất về vẻ đẹp của toán học do nó cho thấy mối liên hệ sâu sắc giữa những con số cơ bản nhất trong toán học. Đồng nhất thức Euler được áp dụng trực tiếp để chứng minh π là số siêu việt và cho thấy bài toán cầu phương hình tròn là không thể giải được.^[55][56] Từ đồng nhất thức trên, ta cũng suy ra trong nhánh đơn trị chính của logarit,^[54]

${\displaystyle \ln(-1)=i\pi .}$

Ngoài ra, khi áp dụng các công thức lũy thừa, ta có

${\displaystyle (\cos x+i\sin x)^{n}=\left(e^{ix}\right)^{n}=e^{inx}=\cos(nx)+i\sin(nx)}$

với mọi số nguyên n, cũng chính là công thức de Moivre.^[57]

Hai biểu thức biểu diễn sin x và cos x theo hàm mũ có thể được suy ra từ chuỗi Taylor ở trên:^[54]

${\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}},\qquad \cos x={\frac {e^{ix}+e^{-ix}}{2}}.}$

Biểu thức cos x + i sin x đôi khi còn được viết tắt là cis(x).^[58][57]

Biểu diễn

Bài chi tiết: Danh sách biểu diễn của e

Số e có thể được biểu diễn theo nhiều cách khác nhau, dưới dạng chuỗi vô hạn, tích vô hạn, liên phân số hay giới hạn của một dãy. Ngoài giới hạn và chuỗi đã cho ở trên, e còn có dạng liên phân số^[59][60]

${\displaystyle e=[2;1,2,1,1,4,1,1,6,1,...,1,2n,1,...]}$ (dãy số A003417 trong bảng OEIS)

hoặc được viết thành

${\displaystyle e=2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{4+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}}}}}}}.}$

Tích vô hạn sau có giá trị bằng e:^[28]

${\displaystyle e={\frac {2}{1}}\left({\frac {4}{3}}\right)^{1/2}\left({\frac {6\cdot 8}{5\cdot 7}}\right)^{1/4}\left({\frac {10\cdot 12\cdot 14\cdot 16}{9\cdot 11\cdot 13\cdot 15}}\right)^{1/8}\cdots .}$

Nhiều cách biểu diễn khác của e dưới dạng chuỗi, dãy số, liên phân số và tích vô hạn cũng đã được chứng minh.

Biểu diễn ngẫu nhiên

Ngoài các biểu thức giải tích chính xác, e còn có thể được tính gần đúng thông qua kỹ thuật ngẫu nhiên. Một trong những kỹ thuật đó bắt nguồn từ việc cho trước một dãy vô hạn các biến độc lập ngẫu nhiên X₁, X₂,... lấy từ phân phối đều trên [0, 1]. Gọi V là số n nhỏ nhất để tổng của n quan sát đầu tiên lớn hơn 1:

${\displaystyle V=\min \left\{n\mid X_{1}+X_{2}+\cdots +X_{n}>1\right\}.}$

Khi đó giá trị kỳ vọng của V là e hay E(V) = e.^[61][62]

Số chữ số đã biết

Số chữ số đã biết của e đã tăng lên đáng kể từ khi máy tính được phát minh do sự gia tăng hiệu suất máy tính và nhiều cải tiến về thuật toán.^[63][64]

Số chữ số thập phân đã biết của e

Năm	Số chữ số	Tính toán thực hiện bởi
1690	1	Jacob Bernoulli[11]
1714	13	Roger Cotes[65]
1748	23	Leonhard Euler[66]
1853	137	William Shanks[67]
1871	205	William Shanks[68]
1884	346	J. Marcus Boorman[69]
1926	707	Derrick Henry Lehmer[70]
1944	808	Peder Pedersen[71]
1949	2.010	John von Neumann (trên ENIAC)[72]
1961	100.265	Daniel Shanks và John Wrench[73]
1978	116.000	Steve Wozniak trên Apple II[74]

Từ khoảng năm 2010, sự ra đời của máy tính để bàn hiện đại tốc độ cao đã làm tăng tính khả thi của quá trình tính toán hàng nghìn tỷ chữ số của e trong một khoảng thời gian chấp nhận được. Tính đến ngày 24 tháng 12 năm 2023, e đã được tính đến 35 nghìn tỷ chữ số thập phân.^[75]

Tính toán chữ số

Một cách để tìm các chữ số của e là thông qua chuỗi^[28]

${\displaystyle e=\sum _{k=0}^{\infty }{\frac {1}{k!}}.}$

Có một kỹ thuật tính toán nhanh hơn sử dụng hai hàm đệ quy p(a, b) và q(a, b) định nghĩa như sau:

${\displaystyle {\binom {p(a,b)}{q(a,b)}}={\begin{cases}{\binom {1}{b}},&{\text{nếu }}b=a+1{\text{,}}\\{\binom {p(a,m)q(m,b)+p(m,b)}{q(a,m)q(m,b)}},&{\text{nếu ngược lại, trong đó }}m=\lfloor (a+b)/2\rfloor .\end{cases}}}$

Biểu thức

${\displaystyle 1+{\frac {p(0,n)}{q(0,n)}}}$

cho giá trị là tổng từng phần thứ n của chuỗi nói trên. Phương pháp này sử dụng phép chia đôi để tính e với số phép toán số học một chữ số ít hơn và giảm độ phức tạp bit xuống. Kết hợp kỹ thuật trên cùng các phương pháp nhân số nguyên dựa trên biến đổi Fourier nhanh giúp quá trình tính toán chữ số của e được thực hiện rất nhanh chóng.^[28]

Trong văn hóa máy tính

Trong sự xuất hiện của văn hóa Internet, nhiều tổ chức và cá nhân đã đôi lúc tỏ lòng kính trọng và tôn vinh số e. Một trong những ví dụ đầu tiên là khi nhà khoa học máy tính Donald Knuth cho số phiên bản của phần mềm Metafont do ông phát triển tiến dần về số e. Các phiên bản lần lượt là 2, 2.7, 2.71, 2.718,...^[76] Một ví dụ khác là hồ sơ IPO của Google năm 2004, trong đó công ty đặt mục tiêu huy động được đúng 2.718.281.828 đô la Mỹ, tức là e tỷ đô la làm tròn đến hàng đơn vị.^[77]

Google cũng đã từng làm một biển quảng cáo đặt tại trung tâm thung lũng Silicon và sau đó tại Cambridge, Massachusetts, Seattle, Washington và Austin, Texas, trong đó ghi "{first 10-digit prime found in consecutive digits of e}.com" (tạm dịch "{số nguyên tố có 10 chữ số đầu tiên trong dãy chữ số liên tiếp của e}.com").^[78] Số nguyên tố có 10 chữ số đầu tiên trong e là 7427466391, bắt đầu từ chữ số thứ 99.^[79] Khi giải được bài toán và truy cập vào website được quảng cáo (hiện không còn tồn tại) thì người giải được dẫn đến một bài toán khó hơn là tìm số thứ năm trong dãy số 7182818284, 8182845904, 8747135266, 7427466391. Dãy số này bao gồm các số có 10 chữ số thuộc dãy chữ số liên tiếp của e có tổng các chữ số bằng 49. Số thứ năm cần tìm trong dãy là 5966290435, bắt đầu từ chữ số thứ 127.^[80] Sau khi giải bài toán thứ hai thì người truy cập được dẫn đến trang web Google Labs để có cơ hội nộp sơ yếu lý lịch.^[81]

Phiên bản chính thức cuối cùng của trình thông dịch Python 2 là 2.7.18, một mã số phiên bản gần giống nhất với giá trị xấp xỉ của e.^[82]

Xem thêm

• Pi