内心有三线 ,这就是说,从三角形
,这就是说,从三角形 的内心到边
的内心到边 、
、 、
、 的有向距离和实际距离有序三元组
的有向距离和实际距离有序三元组 成比例,这里
成比例,这里 是三角形
是三角形 内切圆的半径。注意到记号
内切圆的半径。注意到记号 用比例冒号区分三线和实际有向距离。实际距离有序三元组
用比例冒号区分三线和实际有向距离。实际距离有序三元组 ,能从比例
,能从比例 得到,利用面积关系不难算得
得到,利用面积关系不难算得

这里 ,
,  ,
,  分别是边长
分别是边长 、
、 、
、 ,
, 的面积。(“逗号记法”应该避免使用。因为记号
的面积。(“逗号记法”应该避免使用。因为记号 意味着是一个有序三元组,不允许
意味着是一个有序三元组,不允许 之类运算;然而“比号记法”允许
之类运算;然而“比号记法”允许 。)
。)
设 、
、 和
和 不仅表示三角形的顶点,也是在相应顶点的角。一些熟知点的三线如下:
不仅表示三角形的顶点,也是在相应顶点的角。一些熟知点的三线如下:
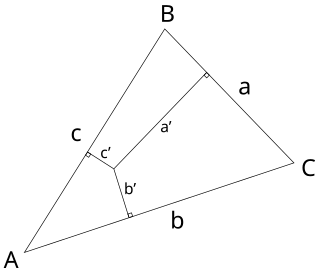



- 内心

- A-旁心

- B-旁心

- C-旁心

- 外心

- 垂心

- 九点圆圆心

- 重心

- 类似重心

注意到,内心一般不是重心,重心有重心坐标1:1:1(它们和实际有向面积 、
、 、
、 成比例,这里
成比例,这里 重心)。
重心)。























































