扭棱四角反角柱

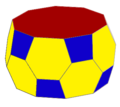
扭棱四角反角柱（英文：Snub square antiprism）是约翰逊多面体的其中一个，其所引为J₈₅^[1]。它无法由帕雷托立体（正多面体）和阿基米得立体（半正多面体）经过切割、增补而得来。扭棱四角反角柱是约翰逊多面体中的基本立体之一。约翰逊多面体是凸多面体，面皆由正多边形组成但不属于均匀多面体，共有92种。这些立体最早在1966年由诺曼·约翰逊（英语：Norman Johnson (mathematician)）（Norman Johnson）命名并给予描述^[2]。

扭棱四角反角柱

类别	约翰逊多面体 J84 - J85 - J86
识别
名称	扭棱四角反角柱
参考索引	J85
鲍尔斯缩写 （verse-and-dimensions的wikia：Bowers acronym）	snisquap
数学表示法
施莱夫利符号	ss{2,8}
性质
面	26
边	40
顶点	16
欧拉特征数	F=26, E=40, V=16 （χ=2）
组成与布局
面的种类	8+16个三角形 2个正方形
顶点图	8个(35) 8个(34.4)
对称性
对称群	D4v群
特性
凸多面体
图像
（展开图）

性质

扭棱四角反角柱共由26个面、40条边和16顶点所组成^[3][4][5]。在其26个面中，有24个三角形和2个正方形^[3]。在其16个顶点中，有8个顶点是5个三角形的公共顶点^[5]，在顶点图中可以用[3⁵]来表示^[6]、另外8个顶点是4个三角形和1个正方形的公共顶点^[5]，在顶点图中可以用[3⁴,4]来表示^[6]。

构造

形如其名地，扭棱四角反角柱可以透过将四角反角柱套用扭棱变换来构造。在施莱夫利符号中可以表示为ss{2,8}，其中s{2,8}是四角反角柱^[7]，其中的扭棱是考克斯特扭棱；而在康威扭棱中，扭棱四角反角柱可以透过将四角锥套用康威扭棱来构造，在康威多面体表示法中可以表示为sY4^[8]。

体积与表面积

若一个扭棱四角反角柱边长为${\displaystyle a}$，则其表面积${\displaystyle A}$为：^[9]

${\displaystyle A=\left(2+6{\sqrt {3}}\right)a^{2}\approx 12.39230a^{2},}$^[10]

而其体积${\displaystyle V}$为：

${\displaystyle V=\xi a^{3},}$

其中${\displaystyle \xi \approx 3.60122}$是下列多项式的最大实根：

${\displaystyle 531441x^{12}-85726026x^{8}-48347280x^{6}[phone]x^{4}+4759488x^{2}-892448.}$^[11]

顶点坐标

令${\displaystyle k}$为下列三次式的正实根，约为${\displaystyle k\approx 0.82354}$：

${\displaystyle 9x^{3}+3{\sqrt {3}}\left(5-{\sqrt {2}}\right)x^{2}-3\left(5-2{\sqrt {2}}\right)x-17{\sqrt {3}}+7{\sqrt {6}}.}$

和h约为${\displaystyle h\approx 1.35374}$：

${\displaystyle h={\frac {{\sqrt {2}}+8+2{\sqrt {3}}k-3\left(2+{\sqrt {2}}\right)k^{2}}{4{\sqrt {3-3k^{2}}}}}.}$

则边长为2的扭棱四角反角柱的顶点坐标由下列顶点的轨道的并集在绕z轴旋转90°和绕垂直于z轴并与x轴夹角22.5°的直线旋转180°所产生的空间对称群之群作用下给出：^[12]

${\displaystyle (1,1,h),\,\left(1+{\sqrt {3}}k,0,h-{\sqrt {3-3k^{2}}}\right)}$

扭棱反角柱

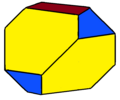
类似的造方式之多面体还有扭棱三角反角柱（施莱夫利符号：ss{2,6}）为经过扭棱变换的三角反角柱（可以视为一个对称性较低的正八面体），其结果为伪二十面体（可以视为一个对称性较低的正二十面体）。另一个为扭棱五角反角柱（施莱夫利符号：ss{2,10}）甚至是更高边数的扭棱反角柱，但其结果不会是由正三角形构成的凸多面体。边数更少的扭棱二角反角柱（施莱夫利符号：ss{2,4}）对应另一个约翰逊多面体——扭棱锲形体，但必须在二角反角柱中保留两个退化的对角面（以红色绘制）。这些都可以视为一系列扭棱反角柱无穷序列的一项。^[7]

扭棱反角柱

对称性	D2d, [2+,4], (2*2)	D3d, [2+,6], (2*3)	D4d, [2+,8], (2*4)	D5d, [2+,10], (2*5)
反角柱	s{2,4} A2 （顶点：4、 边：8、 面：6）	s{2,6} A3 （页面存档备份，存于互联网档案馆） （顶点：6、 边：12、 面：8）	s{2,8} A4 （页面存档备份，存于互联网档案馆） （顶点：8、 边：16、 面：10）	s{2,10} A5 （页面存档备份，存于互联网档案馆） （顶点：10、 边：20、 面：12）
截角反角柱	ts{2,4} tA2 （顶点：16、边：24、面：10）	ts{2,6} tA3 （页面存档备份，存于互联网档案馆） （顶点：24、 边：36、 面：14）	ts{2,8}（英语：truncated square antiprism） tA4 （页面存档备份，存于互联网档案馆） （顶点：32、 边：48、 面：18）	ts{2,10} tA5 （页面存档备份，存于互联网档案馆） （顶点：40、 边：60、 面：22）
对称性	D2, [2,2]+, (222)	D3, [3,2]+, (322)	D4, [4,2]+, (422)	D5, [5,2]+, (522)
扭棱反角柱	J84	二十面体	J85	凹
		sY3 （页面存档备份，存于互联网档案馆） = HtA3	sY4 （页面存档备份，存于互联网档案馆） = HtA4	sY5 （页面存档备份，存于互联网档案馆） = HtA5
	ss{2,4} （顶点：8、 边：20、 面：14）	ss{2,6} （顶点：12、 边：30、 面：20）	ss{2,8} （顶点：16、 边：40、 面：26）	ss{2,10} （顶点：20、 边：50、 面：32）

参见

• 约翰逊多面体
• 多面体
• 帕雷托立体
• 半正多面体