拱线进动

此条目介绍的是天体轨道的旋转。关于旋转轴进动，请见“轴向进动”。关于轨道倾角的变化，请见“轨道倾角变化”。

拱线进动（或拱线前进）是在天体力学中^[1]连接天体轨道拱点的线（拱线）的进动（逐渐旋转）。拱点是轨道上距离其主天体最远（远点）和最近（近点）的点。拱线进动是近心点幅角（近点幅角）的第一个时间导数，是轨道的六个主要轨道元素之一。当轨道轴线与轨道运动方向相同时，视为正拱线进动。拱线转动周期是轨道前进360°所需的时间间隔^[2]，它使地球绕轨道运行约112,000年，完成一个周期并返回相同的方向^[3]。

每一颗围绕太阳运行的行星都遵循一个椭圆轨道，该轨道随时间逐渐旋转（拱线进动）。此图显示了正的近日点进动（近日点的前进），轨道轴与行星的轨道运动方向相同。为了视觉化，这个椭圆的离心率和轨道的进动率被夸大了。太阳系中的大多数轨道离心率低得多，进动速度慢得多，使其接近圆形和静止。

主要的轨道元素（或参数）。拱点的线以蓝色显示，并用ω表示。拱线进动是ω随时间的变化率， dω/dt.

月球绕地球轨道动画-极地视图
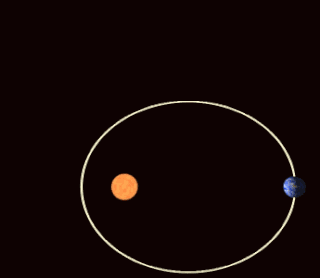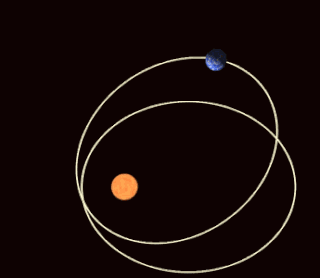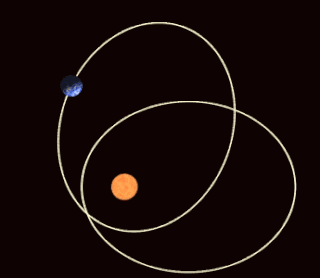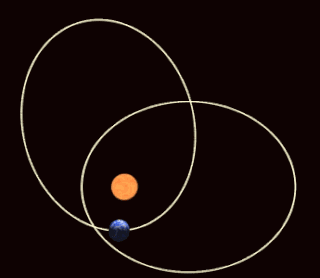
  月球 ·   地球

历史

古希腊天文学家喜帕恰斯注意到月球轨道的拱线进动（即月球远地点的公转，周期约为8.85年）^[4]；它在安提基特拉机械（约公元前80年）中进行了校正（假设值为8.88年/整个周期，校正到当前测量值的0.34%以内）^[5]。太阳拱线的进动（作为一种不同于分点进动的运动）在二世纪由亚历山大的托勒密首次量化。他还计算了进动对天体运动的影响^[6][7][8]。地球和其它行星的拱线进动是众多现象的结果，其中一部分一直很难解释，直到20世纪水星拱线进动的最后一个未知部分才被准确解释。

计算

多种因素可能导致近星点进动，如广义相对论、恒星四极矩、恒星-行星相互潮汐变形和其它行星的摄动^[9]。

ω_total = ω_{General Relativity} + ω_quadrupole + ω_tide + ω_{perturbations}

对于水星，由于一般相对论效应，近日点进动率为每世纪43″（弧秒）。相较之下，由于太阳系其它行星的摄动而产生的进动为每世纪532″，而太阳的扁率（四极矩）造成的贡献可忽略不计，为每世纪0.025″^[10][11]。

根据经典力学，如果恒星和行星被认为是纯球形质量，那么它们将服从一个简单的1/r² 平方反比定律，将力与距离联系起来，从而根据伯特兰定理执行闭合椭圆轨道。非球形质量效应是由外部势能的应用引起的：旋转体的离心势能导致两极之间的扁平化，附近质量的重力引起潮汐凸起。旋转和净潮汐凸起产生引力四极场 （1/r³）导致轨道进动。 仅考虑最低阶效应，孤立的非常热木星的总拱线进动是，并且大致按重要性顺序排列

ω_total = ω_{tidal perturbations} + ω_{General Relativity} + ω_{rotational perturbations} + ω_{rotational *} + ω_{tidal *}

行星潮汐凸起是主导项，超过广义相对论和恒星四极的影响超过一个数量级。潮汐凸起的良好近似结果有助于了解这些行星的内部。对于周期最短的行星，行星内部每年会产生几度的进动。WASP-12b每年的角度高达19.9°^[12][13]。

牛顿旋转轨道定理

主条目：牛顿旋转轨道定理

牛顿汇出了一个早期的定理，试图解释拱线进动。这个定理是“历史上”值得注意的，但它从未被广泛使用，它提出了被发现不存在的力，使这个定理无效。直到1995年，这一旋转轨道定理在三个多世纪的时间里基本上一直是未知的和未开发的^[14]。 牛顿提出，在不影响粒子径向运动的情况下，粒子角运动的变化可以通过添加一个力来解释，该力以距离的倒数变化^[15]。牛顿使用泰勒级数的前身，将他的定理推广到所有的力定律，前提是与圆形轨道的偏差很小，这对太阳系中的大多数行星都有效^{[来源请求]}。然而，在不放弃牛顿万有引力定律的平方反比定律的情况下，他的定理并没有解释月球的拱线进动。此外，通过牛顿旋转轨道定理计算的拱线进动率不如通过摄动理论等较新方法计算的准确^{[来源请求]}。

轨道随时间的变化。

广义相对论

主条目：广义相对论中的开普勒问题

这是在广义相对论中，行星随着轨道的变化进行运行的模拟环绕图

行星水星的近日点近动在19世纪中期被于尔班·勒威耶注意到，并由爱因斯坦的广义相对论解释。

1910年代，有几个人根据狭义相对论计算了近日点的进动。他们通常获得的值仅为正确值的1/6，即7''/年^[16][17]。

爱因斯坦证明，对于一颗行星，其轨道的半长轴为{mvar|a}}，轨道的离心率为{mvar|e}}，公转周期为T，那么在弧度的一个旋转周期内，相对论效应引起的拱线进动为

${\displaystyle \varepsilon =24\pi ^{3}{\frac {a^{2}}{T^{2}c^{2}\left(1-e^{2}\right)}}}$

此处的c是光速^[18]。以水星为例，长轴的一半大约7010579000000000000♠5.79×10¹⁰ 米，其轨道离心率为0.206，公转周期为87.97天或7006760000000000000♠7.6×10⁶ s。从这些和光速（其值是〜7008300000000000000♠3×10⁸ m/s），可以计算出一个公转周期内的拱线进动为ε = 6993502800000000000♠5.028×10⁻⁷弧度 （6995288000000000000♠2.88×10⁻⁵度或0.104″）。在一百年内，水星绕太阳旋转约415圈，因此在这段时间内，由于相对论效应，拱线进动约为43〃，这几乎与之前测量值中无法解释的部分完全对应。

长期气候

地球的拱线进动缓慢地增加了它的近心点幅角；椭圆相对于恒星旋转一次大约需要7005112000000000000♠112,000年^[19]。相对于恒星，地球的极轴，以及至点和分点，以大约7004260000000000000♠26,000年的周期前进。这两种形式的“岁差”结合在一起，使椭圆耗时在7004208000000000000♠20,800和7004290000000000000♠29,000年（平均而言是7004230000000000000♠23,000年）相对于春分点旋转一次，也就是说，近日点返回到同一日期（给定一个完美跟踪季节的民用历）^[20]。

这种异常和热带循环之间的相互作用在地球上的长期气候变化中很重要，称为米兰科维奇循环。米兰科维奇循环是理解拱线进动效应的核心。 在火星也有相等的现象。

右图说明了岁差对北半球季节的影响，相对于近日点和远日点。 请注意，在特定季节扫过的区域会随时间变化。轨道力学要求季节的长度与季节象限的扫掠面积成比例，因此当轨道离心率极端时，轨道远端的季节持续时间可能会更长。

为了便于观察，夸大了轨道上的离心率和近日心率与近日点对季节的影响。显示的季节在北半球，在轨道运行期间的任何给定时间，南半球的季节都将相反。随之而来的一些气候影响主要是由于南半球普遍存在的海洋。

相关条目

• 轴向进动
• 节点进动
• 下摆线
• 罗塞塔（轨道）
• 螺旋描记器