畸变

此条目介绍的是影像上在投影后的变化。关于其他信号的变化，请见“失真”。

在几何光学中，畸变（英语：distortion）是光学系统的横向放大率随物点光束的主光线和主光轴间所成的夹角而变，致使像的几何形状与物不能严格相似的现象。畸变成像偏离直线投影（英语：rectilinear projection）（直线在投影后仍维持直线的投影），属于一种像差，即在像场中横向放大率随着离光轴的距离改变而改变的一种像差。

当横向放大率随夹角增加而增大时，所产生的畸变称为正畸变（positive distortion）或称枕形畸变 （pillow distortion），反之为负畸变（negative distortion）或称桶形畸变（barrel distortion）^[1][2]。

畸变和球面像差、彗形像差、色差、佩兹瓦尔像场弯曲及像散不同，后面几种像差会影响影像的精细度，但不会改变图案（直线在投影后仍是直线，但会因为像差而变模糊），而畸变会改变图案本身形状。畸变与物像点离光轴的垂直高度的立方成正比，因此，物像四角的畸变比物像的四边的畸变程度大^[3]:56。

分类

桶形

枕形

胡形

畸变的例子

畸变可能是不规则的，且有许多不同的模式。但很常见的畸变是辐射对称的，是因为镜头的对称性所产生。这类畸变可以分为桶形畸变或枕形畸变^[4][5]。

桶形畸变

桶形畸变（barrel distortion）下，影像的放大率随着和光轴的距离减少。看到的效果是类似影像放在球面（或木桶）上的效果。鱼眼镜头可以取半个球面的影像，就是利用这种畸变将无穷宽的视野缩到有限的区域内。变焦镜头的桶形畸变出现在一半焦距的位置，在广角范围的端点最严重^[6]。 凹球面透镜较常出现桶形畸变。

枕形畸变

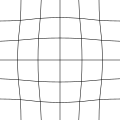
枕形畸变（pincushion distortion），影像的放大率随着和光轴的距离增加。视觉的效果是不通过图形中心的直线会往内弯曲，类似枕形（英语：pincushion）。 凸球面透镜较常出现枕形畸变。

胡形畸变

胡形畸变（mustache distortion）是上述两种的混合，较少见，但不算非常罕见，在靠近影像中心处是枕形畸变，往外扩展时慢慢变成枕形畸变，在图的上半部的横线会类似翘八字胡（英语：handlebar mustache）。

词语由来

上述畸变的名称来自有类似外形的日常事物。

• 
  在桶形畸变中，直线会往外膨胀，类似木桶。
• 
  在枕形畸变中，方形的四角会往外伸长，类似座垫。
• 
  在胡形畸变中，水平线会先在中心部位突出，再往另一个方向弯曲，类似翘八字胡（英语：handlebar mustache）

出现畸变的情形

globe effect（右边）和没有globe effect（左边）比较的动画

摄影中的畸变特别和变焦镜头有关，特别是大画幅镜头，不过也会在定焦镜头上出现，和其焦距有关。例如佳能 EF 50mm 镜头 f/1.4 在极短焦距下会有桶形畸变。广角镜头可能会出现桶形畸变，且常出现在容易出现在变焦镜头的广角端点，枕形畸变会出现在较旧或是低阶的远摄镜头上。胡形畸变特别会在变焦镜头的视野末端出现，特别是后焦距镜头，最近也在大范围变焦镜头（像是尼康 18–200 mm）上出现。

在光学仪器中（例如双筒望远镜）会有一些枕形畸变，目的是为了抵消globe effect（英语：globe effect）。

径向畸变可以由其对同心圆（例如箭靶）的影响来理解

在理解这类畸变时，需记得这些是径向畸变，探讨的光学系统有旋转对称（省略非径向的缺陷），因此正确的测试影像会是一组均匀分隔的同心圆（类似箭靶）。可以看出这些畸变会让同心圆变成不是均匀分隔。像枕形畸变就是外围的圆圈彼此之间的距离会较远。而桶形畸变就是外围的圆圈彼此之间的距离会较近。

软件修正

有未修正桶形畸变的图（26mm）

桶形畸变已被修正的图（图中的电脑是ENIAC电脑）

径向畸变主要是以低阶径向成分为主^[7]，可以用Brown畸变模型来修正^[8]，因为Conrady早期的研究，也称为Brown–Conrady模型^[9]。 Brown–Conrady模型可以修正径向畸变以及因为各镜头没有对正而产生的切线畸变。切线畸变也称为“离心畸变”。可参考Zhang^[10]有关径向畸变的进一步讨论。Brown-Conrady畸变模型为

$${\displaystyle {\begin{alignedat}{3}x_{\mathrm {u} }=x_{\mathrm {d} }&+(x_{\mathrm {d} }-x_{\mathrm {c} })(K_{1}r^{2}+K_{2}r^{4}+\cdots )+(P_{1}(r^{2}+2(x_{\mathrm {d} }-x_{\mathrm {c} })^{2})\\&+2P_{2}(x_{\mathrm {d} }-x_{\mathrm {c} })(y_{\mathrm {d} }-y_{\mathrm {c} }))(1+P_{3}r^{2}+P_{4}r^{4}\cdots )\\y_{\mathrm {u} }=y_{\mathrm {d} }&+(y_{\mathrm {d} }-y_{\mathrm {c} })(K_{1}r^{2}+K_{2}r^{4}+\cdots )+(2P_{1}(x_{\mathrm {d} }-x_{\mathrm {c} })(y_{\mathrm {d} }-y_{\mathrm {c} })\\&+P_{2}(r^{2}+2(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}))(1+P_{3}r^{2}+P_{4}r^{4}\cdots ),\end{alignedat}}}$$

其中

• ${\displaystyle (x_{\mathrm {d} },\ y_{\mathrm {d} })}$是用特定透镜透视到影像平面的畸变影像点
• ${\displaystyle (x_{\mathrm {u} },\ y_{\mathrm {u} })}$是用理想针孔相机透视到影像平面的无畸变影像点
• ${\displaystyle (x_{\mathrm {c} },\ y_{\mathrm {c} })}$是畸变中心
• ${\displaystyle K_{n}}$是第${\displaystyle n}$次径向畸变系数
• ${\displaystyle P_{n}}$是第${\displaystyle n}$次切线畸变系数
• ${\displaystyle r}$ = ${\displaystyle {\sqrt {(x_{\mathrm {d} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {d} }-y_{\mathrm {c} })^{2}}}}$，畸变点以及畸变中心的欧几里得距离^[7]

桶形畸变的${\displaystyle K_{1}}$会是负值，而枕形畸变对应值则是正值。胡形畸变会有非单调的径向畸变几何数列，在特定的${\displaystyle r}$处会变号。

若要为轴向畸变建模，以下的除法模型^[11]可以有比Brown-Conrady偶数阶模型更准确的结果^[12]。

$${\displaystyle {\begin{aligned}x_{\mathrm {u} }&=x_{\mathrm {c} }+{\frac {x_{\mathrm {d} }-x_{\mathrm {c} }}{1+K_{1}r^{2}+K_{2}r^{4}+\cdots }}\\y_{\mathrm {u} }&=y_{\mathrm {c} }+{\frac {y_{\mathrm {d} }-y_{\mathrm {c} }}{1+K_{1}r^{2}+K_{2}r^{4}+\cdots }},\end{aligned}}}$$

参数和以前定义的相同。针对轴向畸变，此模型比Brown–Conrady模型要好用，需要的项次较少，即可更精确的描述严重的畸变^[12]。若使用此模型，大部分的相机只需要一项即可描述^[13]。

软件可以用图像扭转的作法，对图像加反向的畸变来复原影像。这需要确认已畸变的像素对应未畸变的哪一个像素，因为模型非线性，此对应不是显然的。

畸变或去畸变都需要两组系数，或是找到非线性模型的反函数，一般来言，反函数是没有解析解的。标准的作法包括近似、局部线性化以及迭代法都可以使用。各精准度以及计算需要的资源各有不同。

若是使用一阶的除法模型，其去畸变问题存在解析解^[12]，畸变的像素为

$${\displaystyle {\begin{aligned}x_{\mathrm {d} }&=x_{\mathrm {c} }+{\frac {x_{\mathrm {u} }-x_{\mathrm {c} }}{2K_{1}r_{u}^{2}}}(1-{\sqrt {1-4K_{1}r_{u}^{2}}})\\y_{\mathrm {d} }&=y_{\mathrm {c} }+{\frac {y_{\mathrm {u} }-y_{\mathrm {c} }}{2K_{1}r_{u}^{2}}}(1-{\sqrt {1-4K_{1}r_{u}^{2}}}),\end{aligned}}}$$

其中

• ${\displaystyle r_{u}}$ = ${\displaystyle {\sqrt {(x_{\mathrm {u} }-x_{\mathrm {c} })^{2}+(y_{\mathrm {u} }-y_{\mathrm {c} })^{2}}}}$是点相对中心的欧氏距离。

相关条目

• 歪像
• 视角
• 圆柱透视（英语：Cylindrical perspective）
• 质地梯度（英语：Texture gradient）
• 水下视觉（英语：Underwater vision）
• 晕影
• 球面像差