五阶六边形镶嵌

在几何学中，五阶六边形镶嵌（英语：Order-5 hexagonal tiling）是由六边形组成的双曲面正镶嵌图，在施莱夫利符号中用{6,5}表示。五阶六边形镶嵌即每个顶点皆为五个六边形的公共顶点，顶点周围包含了五个不重叠的六边形，因此无法因此无法在平面作出，但可以在双曲面上作出^[1]，或以正则地区图的形式存在。

五阶六边形镶嵌

庞加莱圆盘模型
类别	双曲正镶嵌
对偶多面体	六阶五边形镶嵌
数学表示法
考克斯特符号 （英语：Coxeter-Dynkin diagram）
施莱夫利符号	{6,5}
威佐夫符号 （英语：Wythoff symbol）	5 | 6 2
组成与布局
顶点图	65
对称性
对称群	[6,5], (*652)
旋转对称群 （英语：Rotation_groups）	[6,5]+, (652)
图像
六阶五边形镶嵌 （对偶多面体）

性质

五阶六边形镶嵌是指每个顶点皆为五个六边形的公共顶点所构成的镶嵌结构。一般而言这种镶嵌结构仅能存在于双曲面上并无穷延伸^[2]。然而透过取出区面的局部将其转成其他亏格的环面则可将其变换为有限的正则地区图^[3]。在施莱夫利符号中五阶六边形镶嵌可以用{6,5}表示，这个符号表是每个顶点皆为五个六边形的公共顶点。而在正则地区图中，五阶六边形镶嵌会表达为{6,5}_p，其中下标的p表示这个正则地区图对应的皮特里多边形为p边形^[4]。

正则地区图

做为有限的正则地区图，五阶六边形镶嵌从亏格为9开始存在^[5]，其中可定向的{6,5}正则地区图有皮特里多边形为六边形、八边形、十边形、十二边形等的正则地区图^[6]，不可定向的有皮特里多边形为四边形、五边形、六边形和十边形的正则地区图^[7]。

五阶六边形{6,5}正则地区图

可定向性	亏格	施莱夫利符号	对应多面体	面数	边数	顶点数
可定向[6]	1	{6,5}	双曲无限面体 （双曲正镶嵌）
	9	{6,5}4	二十面体	20	60	24
		{6,5}10	二十面体	20	60	24
	17	{6,5}8	四十面体	40	120	48
	41	{6,5}10	一百面体	100	300	120
		{6,5}20	一百面体	100	300	120
	45	{6,5}6	一百一十面体	110	330	132
		{6,5}12	一百一十面体	110	330	132
	49	{6,5}6	一百二十面体	120	360	144
	55	{6,5}10	一百三十五面体	135	405	162
	65	{6,5}10	一百六十面体	160	480	192
	81	{6,5}40	二百面体	200	600	240
	89	{6,5}6	二百二十面体	220	660	264
		{6,5}12	二百二十面体	220	660	264
不可定向[7]	10	{6,5}4	十面体	10	30	12
		{6,5}5	十面体	10	30	12
		{6,5}10	十面体	10	30	12
	42	{6,5}5	五十面体	50	150	60
	46	{6,5}6	五十五面体	55	165	66
	50	{6,5}6	六十面体	60	180	72
	50	{6,5}6	六十面体	60	180	72
	66	{6,5}6	八十面体	80	240	96
	90	{6,5}6	一百一十面体	110	330	132

相关多面体与镶嵌

相关多面体

皮特里大十二面体

皮特里大十二面体

以不同颜色表示每个面
类别	皮特里对偶 正则地区图
数学表示法
施莱夫利符号	{5,5/2}π
性质
面	10
边	30
顶点	12
欧拉特征数	F=10, E=30, V=12 （χ=-8）
二面角	(不存在)
对称性
对称群	Ih, H3, [5,3], *532
特性
扭歪、正则

皮特里大十二面体是大十二面体的皮特里对偶，可以透过将原有大十二面体上取皮特里多边形构成，换句话说，皮特里大十二面体为由大十二面体的皮特里多边形构成的立体^[8][9]。由于大十二面体的皮特里多边形为扭歪六边形，因此无法确立其封闭范围，故无法计算其表面积和体积。

大十二面体

皮特里大十二面体

由于大十二面体与小星形十二面体对应相同的正则地区图^[10]，因此皮特里大十二面体对应的正则地区图也与皮特里小星形十二面体相同，皆由10个面、30条边和12个顶点组成^[11]。

皮特里大十二面体是一个不可定向且亏格为10的几何结构^[10]。皮特里大十二面体由10个扭歪六边形组成，每个顶点都是5个扭歪六边形的公共顶点，其对应的正则地区图为五阶六边形镶嵌，并具有五边形的皮特里多边形，在施莱夫利符号中可以用{6,5}₅表示^[10]。

大十二面体的皮特里多边形

构成皮特里大十二面体的扭歪六边形面

皮特里小星形十二面体

皮特里小星形十二面体

以不同颜色表示每个面
类别	皮特里对偶 正则地区图
数学表示法
施莱夫利符号	{5/2,5}π
性质
面	10
边	30
顶点	12
欧拉特征数	F=10, E=30, V=12 （χ=-8）
二面角	(不存在)
对称性
对称群	Ih, H3, [5,3], *532
特性
扭歪、正则

皮特里小星形十二面体是小星形十二面体的皮特里对偶，可以透过将原有小星形十二面体上取皮特里多边形构成，其拓朴结构与皮特里大十二面体同构^[12]。是施莱夫利符号为{6,5}的120阶元素对称性抽象多面体的一种具象化结果^[13]。 皮特里小星形十二面体、小星形十二面体、大十二面体、皮特里大十二面体的关系如下：^[12]

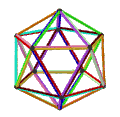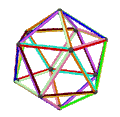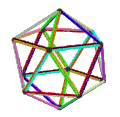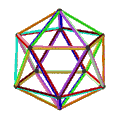${\displaystyle \left\{6,\,{\frac {5}{2}}\right\}}$ 皮特里大十二面体

${\displaystyle {\ce {<->[\pi]}}}$

${\displaystyle \left\{5,\,{\frac {5}{2}}\right\}}$ 大十二面体

${\displaystyle {\ce {<->[\delta]}}}$

${\displaystyle \left\{{\frac {5}{2}},\,5\right\}}$ 小星形十二面体

${\displaystyle {\ce {<->[\pi]}}}$

${\displaystyle \left\{6,\,5\right\}}$ 皮特里小星形十二面体

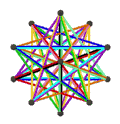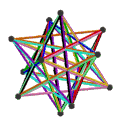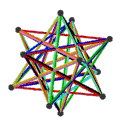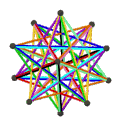其中，“${\displaystyle {\ce {<->[\pi]}}}$”表示互为皮特里对偶；“${\displaystyle {\ce {<->[\delta]}}}$”表示互为对偶多面体。

小星形十二面体

皮特里小星形十二面体

大十二面体与小星形十二面体对应相同的正则地区图^[10]，皆由10个面、30条边和12个顶点组成^[11]，且每个顶点都是5个扭歪六边形的公共顶点，对应的正则地区图同为五阶六边形镶嵌，并具有五边形的皮特里多边形，在施莱夫利符号中可以用{6,5}₅表示^[10]。然而其构成面面有些许不同，且来自不同原像，因此可以被视为{6,5}的不同具象化方式^[13]。

小星形十二面体的皮特里多边形

小星形十二面体的皮特里多边形 正交投影

构成皮特里小星形十二面体 的扭歪六边形面

相关镶嵌图

该镶嵌在拓朴学中也和每个顶点为五个多边形的公共顶点的多面体及镶嵌相关，这类几何结构施莱夫利符号皆为{n,5}、考克斯特符号（英语：Coxeter-Dynkin diagram）为，其中n从2到无穷。^[14]

球面镶嵌		双曲面镶嵌
{2,5}	{3,5}	{4,5}	{5,5}	{6,5}	{7,5}	{8,5}	...	{∞,5}

该镶嵌在拓朴学上顶点图为6⁵，其余顶点图为6ⁿ的几何结构有：^[14]

球面	欧氏	双曲镶嵌
{6,2}	{6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}	...	{6,∞}

五阶六边形镶嵌可以透过康威多面体变换成一系列镶嵌图：

正六边形/五边形镶嵌
对称性：[6,5], (*652)							[6,5]+, (652)	[6,5+], (5*3)	[1+,6,5], (*553)
{6,5}	t{6,5}	r{6,5}	2t{6,5}=t{5,6}	2r{6,5}={5,6}	rr{6,5}	tr{6,5}	sr{6,5}	s{5,6}	h{6,5}
对偶镶嵌
V65	V5.12.12	V5.6.5.6	V6.10.10	V56	V4.5.4.6	V4.10.12	V3.3.5.3.6	V3.3.3.5.3.5	V(3.5)5

[(5,5,3)] 反射对称性均匀镶嵌

参见

• 四阶五边形镶嵌
• 正六边形镶嵌