热门问题
时间线
聊天
视角
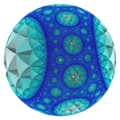
七阶四面体堆砌
来自维基百科,自由的百科全书
Remove ads
在几何学中,七阶四面体堆砌是一种位于双曲三维非紧空间的双曲正堆砌,由正四面体组成,在施莱夫利符号中用{3,3,7}来表示,考克斯特-迪肯符号中以![]()
![]()
![]()
![]()
![]()
![]()
![]() 表示[1] 。每个棱都是七个正四面体的公共棱。
表示[1] 。每个棱都是七个正四面体的公共棱。
性质
由于正四面体不能堆满三维空间,让棱成为五个正四面体的公共棱之后,剩下的空间无法再放入一个正四面体,因此六阶四面体堆砌就只能密铺于双曲空间[2],若再放入一个正四面体则无法存于双曲紧凑空间,即图形发散,无法收敛于无穷远处,也就是说七阶四面体堆砌是一种位于非紧空间的双曲正堆砌,不满足紧空间与仿紧空间的特性。
七阶四面体堆砌的每个棱都是7个正四面体的公共棱、每个顶点都是4个正四面体的公共棱,其在顶点周围的排列方式同为正四面体之面的排列方式,因此七阶四面体堆砌的顶点图为正四面体。此处顶点图的正四面体与七阶四面体堆砌组成胞的正四面体无直接关联,仅是恰巧都是正四面体。
相关多胞体与堆砌
七阶四面体堆砌是一种由正四面体组成的堆砌,其他胞也由正四面体组成多胞体与堆砌或蜂巢体包含:
参见
参考文献
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads