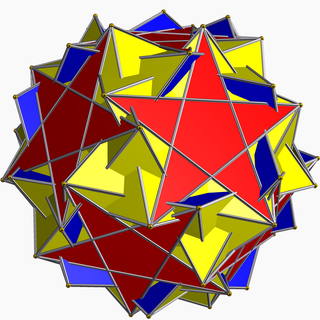
反扭稜小星形十二面體

在幾何學中，反扭稜小星形十二面體是一種星形均勻多面體，索引為U₆₀^[5]，是中逆五角六十面體（英語：Medial inverted pentagonal hexecontahedron）的對偶多面體^[7]，並且與扭稜小星形十二面體拓樸同構^[8]。

反扭稜小星形十二面體

類別	均勻星形多面體
對偶多面體	中逆五角六十面體（英語：Medial inverted pentagonal hexecontahedron）
識別
名稱	反扭稜小星形十二面體 Inverted snub dodecadodecahedron
參考索引	U60, C76, W114
鮑爾斯縮寫 （verse-and-dimensions的wikia：Bowers acronym）	isdid
數學表示法
考克斯特符號 （英語：Coxeter-Dynkin diagram）	[1][2]
施萊夫利符號	sr{5⁄3,5}
威佐夫符號 （英語：Wythoff symbol）	| 5⁄3 2 5[3][4][5] | 2 5⁄3 5[6]:180[7]
性質
面	84
邊	150
頂點	60
歐拉特徵數	F=84, E=150, V=60 （χ=-6）
組成與佈局
面的種類	20個正三角形 12個正五邊形 12個正五角星
頂點圖	3.3.5.3.5⁄3
對稱性
對稱群	Ih, [5,3]+, 532
圖像
3.3.5.3.5⁄3 （頂點圖） 中逆五角六十面體（英語：Medial inverted pentagonal hexecontahedron） （對偶多面體）

性質

反扭稜小星形十二面體共由84個面、150條邊和60個頂點組成^[5]，歐拉示性數為-6^[3]。在其84個面中，有60個正三角形面、12個正五邊形面和12個正五角星面^[9]其60個頂點每個頂點都是1個正十角星、1個五角星和3個三角形的公共頂點，並且這些面在頂都周圍皆是依照三角形、反向相接的五角星、三角形、三角形、五邊形和三角形的順序排列，在頂點圖中可以用(3,5⁄3,3,3,5)^[5][10]、(5⁄3,3,3,5,3)^[1][3]或(5.3.5⁄3.3.3)^[11]來表示。

表示法

反扭稜小星形十二面體在考克斯特—迪肯符號（英語：Coxeter-Dynkin diagram）中可以表示為^[1][2]，在施萊夫利符號中可以表示為sr{5⁄3,5}，在威佐夫記號中可以表示為| 5⁄3 2 5 ^[3][4][5]或| 2 5⁄3 5^[6]:180[7]。

二面角

反扭稜小星形十二面體有三種二面角，分別為五邊形面和三角形面的二面角、三角形面和三角形面的二面角以及五角星面和三角形面的二面角。其中五邊形面和三角形面的二面角的值為多項式4100625 x⁸-32805000 x⁷[phone] x⁶-119799000 x⁵[phone] x⁴-20763000 x³+7189740 x²-2234280 x+201601之正實根（約為0.132650687）的平方根（約為0.36421242）的反餘弦值，約為68.640878254度^[12]；三角形面和三角形面的二面角的值為多項式6561 x⁴-20412 x³+30942 x²-20556 x+4489之正實根（約為0.4216231174）的負平方根的反餘弦值，約為130.490738467度^[12]；五角星面和三角形面的二面角的值為多項式4100625 x⁸-32805000 x⁷[phone] x⁶-119799000 x⁵[phone] x⁴-20763000 x³+7189740 x²-2234280 x+201601之正實根（約為0.9627736877）的平方根（約為0.9812103178）的反餘弦值，約為11.124480107度。^[12]

尺寸

若反扭稜小星形十二面體的邊常為單位長，則其外接球半徑為多項式${\displaystyle 64x^{4}-192x^{3}+180x^{2}-65x+8}$之較小正實根（約為0.72527）的平方根^[12]，約為0.8516302^[13]。

相關多面體

兩個反扭稜小星形十二面體可以複合成均勻複合體，稱為二複合反扭稜小星形十二面體（英語：Compound of two inverted snub dodecadodecahedra）^[14]。

二複合反扭稜小星形十二面體（英語：Compound of two inverted snub dodecadodecahedra）

參見

• 均勻多面體列表（英語：List_of_uniform_polyhedra）
• 扭稜小星形十二面體