热门问题
时间线
聊天
视角
子集
集合A是集合B的子集,是指A的所有元素都是B當中的元素 来自维基百科,自由的百科全书
Remove ads
子集(英語:subset)亦稱部分集合,為某集合中部分元素的集合;這時某集合則被稱作這個子集的超集或母集。子集與超集的關係被稱為「包含」。
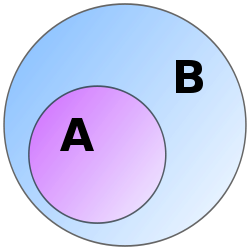
如果集合的任意一個元素都是集合的元素(,亦可寫作),則集合稱為集合的子集,記為或,讀作「集合包含於集合」或「集合包含集合」。
即:,有,則。
若和為集合,且的所有元素都是的元素,則可表示為:
- 是的子集(或稱包含於 );
- 是的超集/母集(或稱包含 );
任何集合皆是自身的子集()。而的子集中不等於的集合,稱為真子集,若是的真子集,寫作。
Remove ads
定義
假設有和兩個集合,如果中的每個元素都在中,則:
- 是的子集,記作
- 也可以說
- 是的超集,記作
如果是的子集,但不等於(即中至少存在一個元素不在中),則:
- 是的真子集,記作
- 也可以說
- 是的真超集,記作
Remove ads
符號
ISO 80000-2標準中定義了兩種符號搭配:[1]
Remove ads
舉例
性質

命題1:空集是任意集合的子集。
這個命題說明:包含是一種偏序關係。
命題2:若是集合,則:
- 自反性:
- 反對稱性:
- 若且,則
- 傳遞性:
- 若且,則
這個命題說明:對任意集合,的冪集按包含排序是一個有界格,與上述命題相結合,則它是一個布爾代數。
命題3:若是集合的子集,則:
- 存在並運算:
- 若且,則
- 存在交運算:
- 若且,則
命題4:對任意兩個集合和,下列表述等價:
Remove ads
參考文獻
參見
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads







































