拋物線的求積

對拋物線的求積（希臘語：Τετραγωνισμὸς παραβολῆς）是古希臘數學家阿基米德的一篇幾何學論文，成文於公元前三世紀。此論文源自阿基米德寄往他的朋友多西修斯的信中（其中包括有關拋物線的24個命題），最終證明了拋物線與直線之間的面積是其內切三角形的面積的 ${\displaystyle 4/3}$ 倍。

這裡展現了拋物線圍成的弓形（即需要求的區域）

論文中陳述使用的是窮竭法。阿基米德將所求區域分割成無限個三角形，三角形的面積則形成了一個等比數列。阿基米德計算了這個等比數列的加和，然後證明了這個加和是拋物線圓缺的面積。此為古代數學窮竭法中最精妙的用法，直到17世紀積分學的發展，卡瓦列里的求積公式取代它之前，它一直是無與倫比的。^[1]

理論概述

Archimedes inscribes a certain triangle into the given parabolic segment.

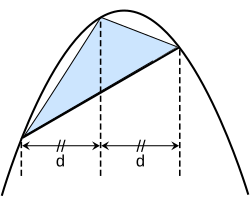
此處的弓形是指由拋物線和直線結合的區域。^[2]為了求得弓形的面積，阿基米德考慮了一個內接確定的三角形，這個三角形的底是拋物線的弦，除弦上兩點之外的三角形第三點在拋物線上的切線平行於弦，根據命題1（拋物線的求積），如果從第三個頂點畫一條平行於軸線的線能將弦分成相等的兩條線段，則拋物線弓形的面積是該內接三角形面積的4/3。

論文結構

阿基米德給出了主定理的兩個證明。 第一種使用力學，阿基米德認為，當放置在適當的槓桿上的一個位置上時，線段的「重量」將能夠平衡三角形的「重量」。 第二個更著名的證明是使用純幾何，特別是窮竭法。

在這二十四個命題中，前三個命題都未經歐幾里得的《圓錐曲線要點》（歐幾里得在圓錐曲線研究中丟的一部著作）所引用。 命題四和命題五確定了拋物線的基本性質； 命題6至17給出了主定理的機械證明； 命題18至24給出了幾何證明。

幾何證明

分割拋物線

阿基米德的方法：將拋物線弓形分割成任意數量的三角形

證明的主要思想是將拋物線與線段之間的面積分割為無數個三角形。如右圖所示，每一個三角形都以同樣的方式內接於一個拋物線弓形，比如藍色三角形被整個弓形面積所內接，綠色三角形則內接於藍色三角形占據後剩下面積的弓形中。

三角形的面積

在第18至21個命題中，阿基米德證明了每個綠色三角形的面積是藍色三角形面積的八分之一。 從現代數學的角度來看，這是因為綠色三角形的寬度為一半，高度的四分之一。^[3]

通過擴展，每個黃色三角形的面積是綠色三角形的八分之一，每個紅色三角形的面積是黃色三角形的八分之一，依此類推。 使用窮竭法，可以得出拋物線段的總面積為

${\displaystyle {\text{S}}\;=\;T\,+\,2\left({\frac {T}{8}}\right)\,+\,4\left({\frac {T}{8^{2}}}\right)\,+\,8\left({\frac {T}{8^{3}}}\right)\,+\,\cdots .}$

這裡的 T 代表大藍色三角形的面積，第二項代表兩個綠色三角形的總面積，第三項代表四個黃色三角形的總面積，依此類推。 可以很容易的得出^[4]

${\displaystyle {\text{S}}\;=\;\left(1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots \right)T.}$

級數求和

阿基米德證明 1/4 + 1/16 + 1/64 + ... = 1/3

為了完成證明，阿基米德證明了

${\displaystyle 1\,+\,{\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots \;=\;{\frac {4}{3}}.}$

上面的式子是等比數列—每個連續項是前一項的四分之一。在現代數學中，該公式是等比數列的求和公式的特例。

這裡阿基米德使用純粹的幾何的方法求和。^[5]如圖所示。 此圖片顯示了一個單位正方形，該正方形已被分解為多個較小的正方形。 每個連續的紫色方塊的面積為前一個方塊的四分之一，紫色的總面積為總和。

${\displaystyle {\frac {1}{4}}\,+\,{\frac {1}{16}}\,+\,{\frac {1}{64}}\,+\,\cdots .}$

但是，每個紫色正方形和與之對應的一組黃色正方形中的任何一個都全等，因此紫色正方形的面積覆蓋了單位正方形面積的1/3。 因此，上述序列之和為4/3。^[6]

其他

• 無窮小演算
• 1/4 + 1/16 + 1/64 + 1/256 + …