標準偏差

標準偏差^[1][2]（standard deviation，std dev，SD）又稱標準差^[3][4]、中誤差^[5]，在統計學中，是衡量一組變量值相對於其算術平均值（期望值）變異程度（離散程度）的指標^[6]。標準差越小（低），表示這些變量值越傾向於聚集在數據集的算術平均值（也視作期望值）附近；反之，標準差越大（高），則意味著這些變量值分布得越分散。

關於均方差或均方誤差（MSE），請見「均方誤差」。

關於均方根誤差（RMSE），請見「均方根誤差」。

提示：此條目的主題不是標準誤差。

圖中紅藍兩組數據平均值相同，但標準差不同。紅色數據的標準差較藍色數據的標準差要小。

標準差通常用於界定哪些數據屬於異常值（離群值），而哪些不屬於異常值。在數學文本和方程式中，通常用小寫希臘字母 σ 表示母體標準差（population SD），用小寫拉丁字母 s 表示樣本標準差（sample SD）。在實際研究中，我們通常無法獲取母體所有數據，因此會抽取樣本來推斷母體，藉由樣本的變異度來推估計母體的變異度。

在機率統計中，標準差最常作為評估一組數值的離散程度之用。標準偏差（標準差）的操作型定義為：

一群數值與其算術平均數之差異的平方，再取算術平均數，此時得變異數（variance，σ²，s²）又稱方差，最後取二次方根；即「變異數開主平方根」。

標準差可反映組內個體間的離散程度，也可表示內部符合精度，作為在一定條件下衡量測量精度的一種數值指標。標準差與期望值之比為標準離差率。

標準差具有兩種性質：

1. 為非負數值（因為平方後再做平方根）；
2. 與測量資料具有相同單位（這樣才能比對）。

一個總量的標準差或一個隨機變數的標準差，及一個子集合樣品數的標準差之間，有所差別。標準差的概念由卡爾·皮爾森引入到統計中。

闡述及應用

在隨機分布中的離均差

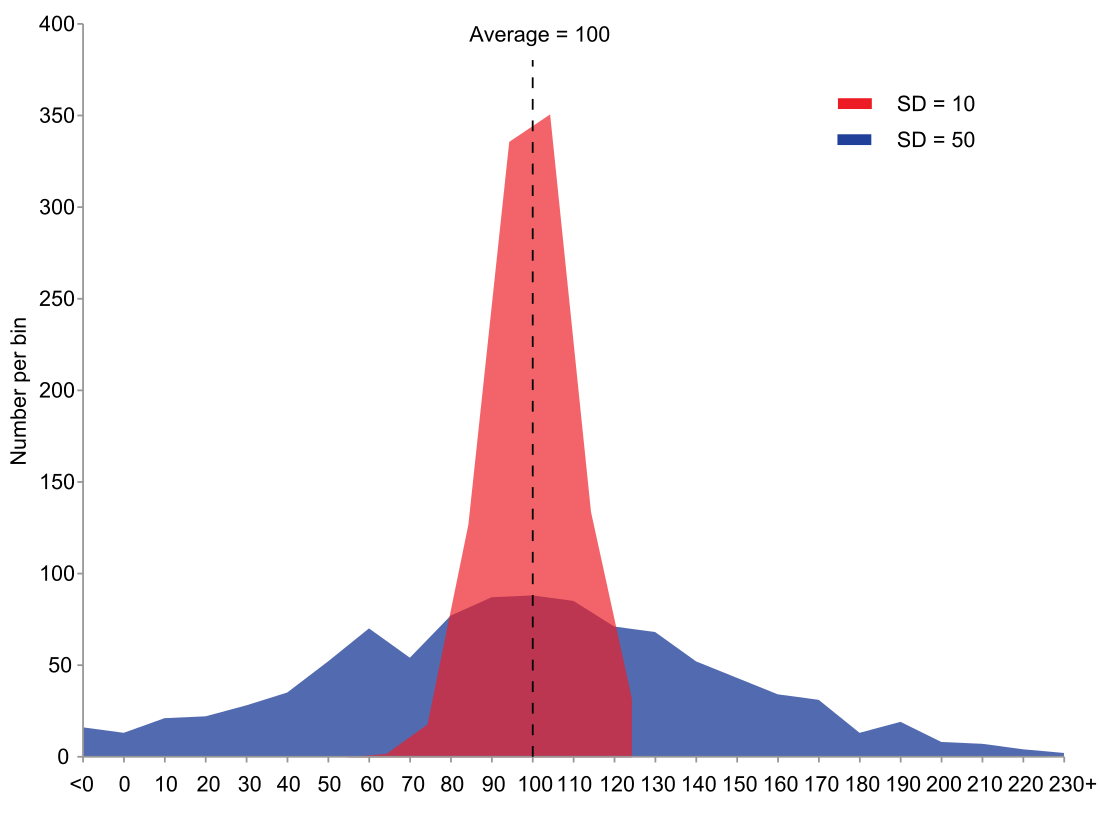
簡單來說，標準差是一組數值自平均值分散開來的程度的一種測量觀念。一個較大的標準差，代表大部分的數值和其平均值之間差異較大；一個較小的標準差，代表這些數值較接近平均值。

例如，兩組數的集合{0, 5, 9, 14}和{5, 6, 8, 9}其平均值都是7，但第二個集合具有較小的標準差。

表述「相差${\displaystyle k}$個標準差」，即在 ${\displaystyle {\overline {X}}\pm kS}$ 的樣本（sample）範圍內考量。

標準差可以當作不確定性的一種測量。例如在物理科學中，做重複性測量時，測量數值集合的標準差代表這些測量的精確度。當要決定測量值是否符合預測值，測量值的標準差佔有決定性重要角色：如果測量平均值與預測值相差太遠（同時與標準差數值做比較），則認為測量值與預測值互相矛盾。這很容易理解，因為如果測量值都落在一定數值範圍之外，可以合理推論預測值是否正確。

標準差應用於投資上，可作為量度回報穩定性的指標。標準差數值越大，代表回報遠離過去平均數值，回報較不穩定故風險越高。相反，標準差數值越小，代表回報較為穩定，風險亦較小。

母體的標準差

基本定義

${\displaystyle \sigma ={\sqrt {{\frac {1}{N}}\sum _{i=1}^{N}(x_{i}-\mu )^{2}}}}$

${\displaystyle \mu }$為平均值。

母體為隨機變數

一隨機變數${\displaystyle X}$的標準差定義為：

${\displaystyle \sigma ={\sqrt {\operatorname {E} ((X-\operatorname {E} (X))^{2})}}={\sqrt {\operatorname {E} (X^{2})-(\operatorname {E} (X))^{2}}}}$

須注意並非所有隨機變數都具有標準差，因為有些隨機變數不存在期望值。 如果隨機變數${\displaystyle X}$為${\displaystyle x_{1},\cdots ,x_{n}}$具有相同機率，則可用上述公式計算標準差。

離散隨機變數的標準差

若${\displaystyle X}$是由實數${\displaystyle x_{1},x_{2},...,x_{n}}$構成的離散隨機變數（英語：discrete random variable），且每個值的機率相等，則${\displaystyle X}$的標準差定義為：

${\displaystyle \sigma ={\sqrt {{\frac {1}{N}}\left[(x_{1}-\mu )^{2}+(x_{2}-\mu )^{2}+\cdots +(x_{N}-\mu )^{2}\right]}}}$　，其中　${\displaystyle \mu ={\frac {1}{N}}(x_{1}+\cdots +x_{N})}$

換成用${\displaystyle \sum }$來寫，就成為：

${\displaystyle \sigma ={\sqrt {{\frac {1}{N}}\sum _{i=1}^{N}(x_{i}-\mu )^{2}}}}$　，其中　${\displaystyle \mu ={\frac {1}{N}}(x_{1}+\cdots +x_{N})}$

目前為止，與母體標準差的基本公式一致。

然而若每個${\displaystyle x_{i}}$可以有不同機率${\displaystyle p_{i}}$，則${\displaystyle X}$的標準差定義為：

${\displaystyle \sigma ={\sqrt {\sum _{i=1}^{N}p_{i}(x_{i}-\mu )^{2}}}}$　，其中　${\displaystyle \mu =\sum _{i=1}^{N}p_{i}x_{i}.}$

這裡，${\displaystyle \mu }$為${\displaystyle X}$的數學期望值。

連續隨機變數的標準差

若${\displaystyle X}$為機率密度${\displaystyle p(X)}$的連續隨機變數（英語：continuous random variable），則${\displaystyle X}$的標準差定義為：

${\displaystyle \sigma ={\sqrt {\int (x-\mu )^{2}\,f(x)\,dx}}}$

其中${\displaystyle \mu }$為${\displaystyle X}$的數學期望值：

${\displaystyle \mu =\int x\,f(x)\,dx}$

標準差的特殊性質

對於常數${\displaystyle c}$和隨機變數${\displaystyle X}$和${\displaystyle Y}$：

${\displaystyle \sigma (X+c)=\sigma (X)}$

${\displaystyle \sigma (cX)=c\cdot \sigma (X)}$

${\displaystyle \sigma (X+Y)={\sqrt {\sigma ^{2}(X)+\sigma ^{2}(Y)+2\cdot {\mbox{cov}}(X,Y)}}}$

其中：

• ${\displaystyle {\mbox{cov}}(X,Y)}$表示隨機變數${\displaystyle X}$和${\displaystyle Y}$的共變異數。
• ${\displaystyle \sigma ^{2}(X)}$表示${\displaystyle [\sigma (X)]^{2}}$，即${\displaystyle Var(X)}$（${\displaystyle X}$的變異數），對${\displaystyle Y}$亦同。

樣本的標準差

在真實世界中，找到一個母體的真實的標準差並不實際。大多數情況下，母體標準差是通過隨機抽取一定量的樣本並計算樣本標準差估計的。

從一大組數值${\displaystyle X_{1},\cdots ,X_{N}}$當中取出一樣本數值組合${\displaystyle x_{1},\cdots ,x_{n}:n<N}$，常定義其樣本標準差：

${\displaystyle s={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}}$

樣本變異數${\displaystyle s^{2}}$是對母體變異數${\displaystyle \sigma ^{2}}$的不偏估計。之所以${\displaystyle s}$中的分母要用${\displaystyle n-1}$而不是像母體樣本差那樣用${\displaystyle n}$，是因為${\displaystyle \left(x_{i}-{\bar {x}}\right)}$的自由度為${\displaystyle n-1}$，這是由於存在約束條件${\displaystyle \sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)=0}$。

範例

這裡示範如何計算一組數的標準差。例如一群孩童年齡的數值為{5, 6, 8, 9}：

• 第一步，計算平均值${\displaystyle {\overline {x}}}$︰

${\displaystyle {\overline {x}}={\frac {1}{N}}\sum _{i=1}^{N}x_{i}}$

當${\displaystyle {\begin{smallmatrix}N=4\end{smallmatrix}}}$（因為集合裏有4個數），分別設為：

${\displaystyle {\begin{aligned}x_{1}&=5,\\x_{2}&=6,\\x_{3}&=8,\\x_{4}&=9,\end{aligned}}}$

則平均值為

${\displaystyle {\begin{aligned}{\overline {x}}&={\frac {1}{4}}\sum _{i=1}^{4}x_{i}&(N=4)\\&={\frac {1}{4}}\left(x_{1}+x_{2}+x_{3}+x_{4}\right)\\&={\frac {1}{4}}\left(5+6+8+9\right)\\&=7.\end{aligned}}}$

• 第二步，計算標準差${\displaystyle \sigma \,}$︰

${\displaystyle {\begin{aligned}\sigma &={\sqrt {{\frac {1}{N}}\sum _{i=1}^{N}(x_{i}-{\overline {x}})^{2}}}\\&={\sqrt {{\frac {1}{4}}\sum _{i=1}^{4}(x_{i}-{\overline {x}})^{2}}}&(N=4)\\&={\sqrt {{\frac {1}{4}}\sum _{i=1}^{4}(x_{i}-7)^{2}}}&({\overline {x}}=7)\\&={\sqrt {{\frac {1}{4}}\left[(x_{1}-7)^{2}+(x_{2}-7)^{2}+(x_{3}-7)^{2}+(x_{4}-7)^{2}\right]}}\\&={\sqrt {{\frac {1}{4}}\left[(5-7)^{2}+(6-7)^{2}+(8-7)^{2}+(9-7)^{2}\right]}}\\&={\sqrt {{\frac {1}{4}}\left((-2)^{2}+(-1)^{2}+1^{2}+2^{2}\right)}}\\&={\sqrt {{\frac {1}{4}}\left(4+1+1+4\right)}}\\&={\sqrt {\frac {10}{4}}}\\&\approx 1.58114\,.\end{aligned}}}$

常態分布的規則

主條目：常態分布

深藍區域是距平均值小於一個標準差之內的數值範圍，在常態分布中，此範圍所佔比率為全部數值之68%；兩個標準差之內（深藍，藍）的比率合起來為95%；三個標準差之內（深藍，藍，淺藍）的比率合起來為99.7%。

在實際應用上，常考慮一組數據具有近似於常態分布的機率分布。若其假設正確，則約68%數值分布在距離平均值有1個標準差之內的範圍，約95%數值分布在距離平均值有2個標準差之內的範圍，以及約99.7%數值分布在距離平均值有3個標準差之內的範圍。稱為「68-95-99.7法則」。

${\displaystyle f(x;\mu ,\sigma ^{2})={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}}$

${\displaystyle {\text{Proportion}}=\operatorname {erf} \left({\frac {z}{\sqrt {2}}}\right)}$

${\displaystyle {\text{Proportion}}\leq x={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {z}{\sqrt {2}}}\right)\right]}$.^[7]

Percentage within(z)

z(Percentage within)

數字比率 標準差值	機率	包含之外比例
	百分比	百分比	比例
0.318 639σ	25%	75%	3 / 4
6999674490000000000♠0.674490σ	7001500000000000000♠50%	7001500000000000000♠50%	1 / 7000200000000000000♠2
6999994458000000000♠0.994458σ	68%	32%	1 / 3.125
1σ	7001682689492000000♠68.2689492%	7001317310508000000♠31.7310508%	1 / 7000315148720000000♠3.1514872
7000128155200000000♠1.281552σ	80%	20%	1 / 5
7000164485400000000♠1.644854σ	90%	10%	1 / 10
7000195996400000000♠1.959964σ	95%	5%	1 / 20
2σ	7001954499736000000♠95.4499736%	7000455002640000000♠4.5500264%	1 / 7001219778950000000♠21.977895
7000257582900000000♠2.575829σ	99%	1%	1 / 100
3σ	7001997300204000000♠99.7300204%	6999269979600000000♠0.2699796%	1 / 370.398
7000329052700000000♠3.290527σ	99.9%	0.1%	1 / 7003100000000000000♠1000
7000389059200000000♠3.890592σ	99.99%	0.01%	1 / 7004100000000000000♠10000
4σ	7001999936660000000♠99.993666%	6997633400000000000♠0.006334%	1 / 7004157870000000000♠15787
7000441717300000000♠4.417173σ	99.999%	0.001%	1 / 7005100000000000000♠100000
7000450000000000000♠4.5σ	99.9993204653751%	0.0006795346249%	1 / 7005147159535800000♠147159.5358 3.4 / 7006100000000000000♠1000000 (每一邊)
7000489163800000000♠4.891638σ	7001999999000000000♠99.9999%	6996100000000000000♠0.0001%	1 / 7006100000000000000♠1000000
5σ	7001999999426697000♠99.9999426697%	6995573303000000000♠0.0000573303%	1 / 7006174427800000000♠1744278
7000532672399999999♠5.326724σ	7001999999900000000♠99.99999%	6995100000000000000♠0.00001%	1 / 7007100000000000000♠10000000
7000573072900000000♠5.730729σ	7001999999990000000♠99.999999%	6994100000000000000♠0.000001%	1 / 7008100000000000000♠100000000
7000600000000000000♠6σ	7001999999998027000♠99.9999998027%	6993197300000000000♠0.0000001973%	1 / 7008506797346000000♠506797346
7000610941000000000♠6.109410σ	7001999999999000000♠99.9999999%	6993100000000000000♠0.0000001%	1 / 7009100000000000000♠1000000000
7000646695100000000♠6.466951σ	7001999999999900000♠99.99999999%	6992100000000000000♠0.00000001%	1 / 7010100000000000000♠10000000000
7000680650200000000♠6.806502σ	7001999999999990000♠99.999999999%	6991100000000000000♠0.000000001%	1 / 7011100000000000000♠100000000000
7σ	99.9999999997440%	6990256000000000000♠0.000000000256%	1 / 7011390682215445000♠390682215445

標準差與平均值之間的關係

一組數據的平均值及標準差常常同時作為參考的依據。從某種意義上說，如果用平均值來考量數值的中心的話，則標準差也就是對統計的分散度的一個「自然」的測度。因為由平均值所得的標準差要小於到其他任何一個點的標準差。較確切的敘述為：設${\displaystyle X_{1},\cdots ,X_{N}}$為實數，定義函數：

${\displaystyle \sigma (\mu )={\sqrt {{\frac {1}{N}}\sum _{i=1}^{N}(x_{i}-\mu )^{2}}}}$

使用微積分或者通過配方法，不難算出${\displaystyle \sigma (\mu )}$在下面情況下具有唯一最小值：

${\displaystyle \mu ={\overline {x}}}$

幾何學解釋

從幾何學的角度出發，標準差可以理解為一個從${\displaystyle n}$維空間的一個點到一條直線的距離的函數。舉一個簡單的例子，一組數據中有3個值，${\displaystyle X_{1},X_{2},X_{3}}$。它們可以在3維空間中確定一個點${\displaystyle P=(X_{1},X_{2},X_{3})}$。想像一條通過原點的直線${\displaystyle L={(r,r,r):r\in \mathbb {R} }}$。如果這組數據中的3個值都相等，則點${\displaystyle P}$就是直線${\displaystyle L}$上的一個點，${\displaystyle P}$到${\displaystyle L}$的距離為0，所以標準差也為0。若這3個值不都相等，過點${\displaystyle P}$作垂線${\displaystyle PR}$垂直於${\displaystyle L}$，${\displaystyle PR}$交${\displaystyle L}$於點${\displaystyle R}$，則${\displaystyle R}$的坐標為這3個值的平均數：

${\displaystyle R=({\overline {x}},{\overline {x}},{\overline {x}})}$

運用一些代數知識，不難發現點${\displaystyle P}$與點${\displaystyle R}$之間的距離（也就是點${\displaystyle P}$到直線${\displaystyle L}$的距離）是${\displaystyle \sigma {\sqrt {3}}}$。在${\displaystyle n}$維空間中，這個規律同樣適用，把${\displaystyle 3}$換成${\displaystyle n}$就可以了。