泰勒斯定理

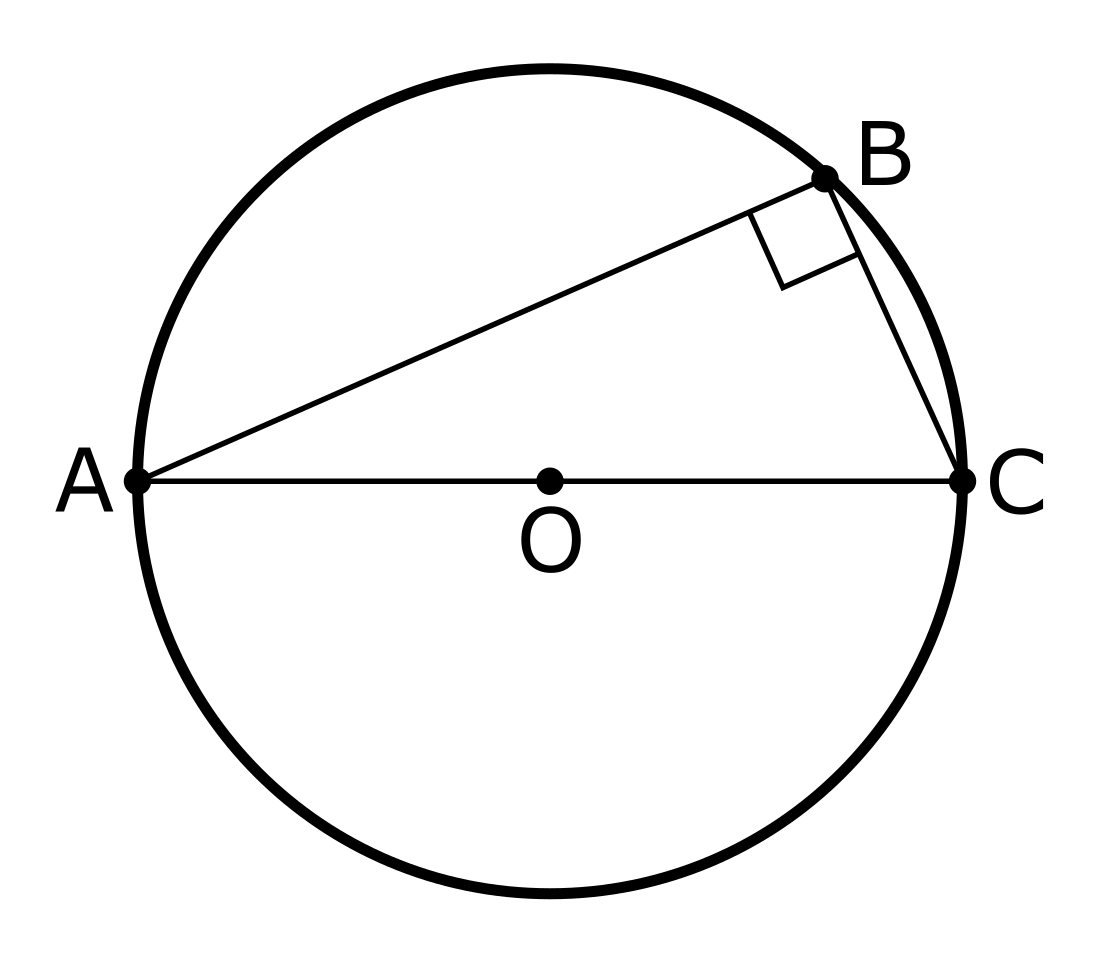
泰勒斯定理（英語：Thales' theorem）以古希臘思想家、科學家、哲學家泰勒斯的名字命名，其內容為：若${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$是圓周上的三點，且${\displaystyle AC}$是該圓的直徑，那麼${\displaystyle \angle ABC}$必然為直角。或者說，直徑所對的圓周角是直角。該定理在歐幾里得《幾何原本》第三卷中被提到並證明^[1]。

泰勒斯定理：如果${\displaystyle AC}$是直徑，那麼${\displaystyle \angle ABC}$是直角。

泰勒斯定理的逆定理同樣成立，即：直角三角形中，直角的頂點在以斜邊為直徑的圓上。

證明

證法一

以下證明主要使用兩個定理：

• 三角形的內角和等於180°
• 等腰三角形的兩個底角相等

• 
  泰勒斯定理的動態演示圖。
• 
  證明圖。

設${\displaystyle O}$為圓心，因為${\displaystyle OA=OB=OC}$，所以${\displaystyle \bigtriangleup OAB}$和${\displaystyle \bigtriangleup OBC}$都是等腰三角形。因為等腰三角形底角相等，故有${\displaystyle \angle OBC=\angle OCB}$，且${\displaystyle \angle BAO=\angle ABO}$。設${\displaystyle \alpha =\angle BAO}$，${\displaystyle \beta =\angle OBC}$。在${\displaystyle \bigtriangleup ABC}$中，因為三角形的內角和等於180°，所以有

${\displaystyle \alpha +\left(\alpha +\beta \right)+\beta =180^{\circ }}$

${\displaystyle {2}\alpha +{2}\beta =180^{\circ }}$

${\displaystyle {2}(\alpha +\beta )=180^{\circ }}$

${\displaystyle \therefore \angle ABC=\alpha +\beta =90^{\circ }.}$

證法二

泰勒斯定理也可以用三角學方法證明，證明如下：

令${\displaystyle O=(0,0)}$, ${\displaystyle A=(-1,0)}$, ${\displaystyle C=(1,0)}$。此時，${\displaystyle B}$就是單位圓${\displaystyle (\cos \theta ,\sin \theta )}$上的一點。我們將通過證明${\displaystyle AB}$與${\displaystyle BC}$垂直，即它們的斜率之積等於–1，來證明這個定理。計算${\displaystyle AB}$和${\displaystyle BC}$的斜率：

${\displaystyle m_{AB}={\frac {y_{B}-y_{A}}{x_{B}-x_{A}}}={\frac {\sin \theta }{\cos \theta +1}}}$

${\displaystyle m_{BC}={\frac {y_{B}-y_{C}}{x_{B}-x_{C}}}={\frac {\sin \theta }{\cos \theta -1}}}$

並證明它們的積等於–1:

${\displaystyle {\begin{aligned}&m_{AB}\cdot m_{BC}\\=&{\frac {\sin \theta }{\cos \theta +1}}\cdot {\frac {\sin \theta }{\cos \theta -1}}\\=&{\frac {\sin ^{2}\theta }{\cos ^{2}\theta -1}}\\=&{\frac {\sin ^{2}\theta }{-\sin ^{2}\theta }}\\=&-1\end{aligned}}}$

注意以上證明過程中運用了畢達哥拉斯三角恆等式${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}$。

逆定理的證明

此證明使用兩線的向量形成直角三角形，若且唯若其內積為零。設有直角三角形${\displaystyle ABC}$，和以${\displaystyle AC}$為直徑的圓${\displaystyle O}$。設${\displaystyle O}$在原點，以方便計算。則${\displaystyle AB}$和${\displaystyle BC}$的內積為：

${\displaystyle (A-B)\cdot (B-C)=(A-B)\cdot (B+A)=|A|^{2}-|B|^{2}=0}$

${\displaystyle |A|=|B|}$

故${\displaystyle A}$和${\displaystyle B}$與圓心等距，即${\displaystyle B}$在圓上。

一般化以及有關定理

泰勒斯定理是「同弧所對的圓周角是圓心角的一半」的一個特殊情況。

以下是泰勒斯定理的一個相關定理：

如果${\displaystyle AC}$是一個圓的直徑，則：

• 若${\displaystyle B}$在圓內，則${\displaystyle \angle ABC>90^{\circ }}$
• 若${\displaystyle B}$在圓上，則${\displaystyle \angle ABC=90^{\circ }}$
• 若${\displaystyle B}$在圓外，則${\displaystyle \angle ABC<90^{\circ }}$

歷史

泰勒斯並非此定理的首名發現者，古埃及人和巴比倫人一定已知這特性，可是他們沒有給出證明。