拉回 (範疇論)

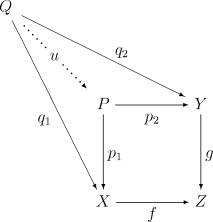
在數學分支範疇論中，拉回（也稱為纖維積或笛卡爾方塊）是由具有公共上域的兩個態射 ${\displaystyle f:X\rightarrow Z}$ 與 ${\displaystyle g:Y\rightarrow Z}$ 組成的圖表的極限。拉回經常寫作

${\displaystyle P=X\times _{Z}Y.\,}$

泛性質

明確地說，態射 ${\displaystyle f}$ 和 ${\displaystyle g}$ 的拉回由一個對象 ${\displaystyle P}$ 和兩個態射 ${\displaystyle p_{1}:P\rightarrow X}$與 ${\displaystyle p_{2}:P\rightarrow Y}$ 組成，使得圖表

交換。並且拉回 ${\displaystyle (P,p_{1},p_{2})}$ 對這個圖表必須是通用的。這便是說，任何其它這樣的三元組 ${\displaystyle (Q,q_{1},q_{2})}$ 一定存在惟一的 ${\displaystyle u:Q\rightarrow P}$ 使得圖表

交換。和所有泛構造一樣，拉回如果存在必然在同構的意義下是惟一的。

弱拉回

一個cospan ${\displaystyle X\rightarrow Z\leftarrow Y}$ 的弱拉回是在cospan上面的錐只須滿足弱泛性質，這就是說中間映射 ${\displaystyle u:Q\rightarrow P}$ 不必是惟一的。

例子

在集合範疇中，${\displaystyle f}$ 與 ${\displaystyle g}$ 的拉回是集合

${\displaystyle X\times _{Z}Y=\{(x,y)\in X\times Y|f(x)=g(y)\},\,}$

以及投影映射的限制 ${\displaystyle \pi _{1}}$ 與 ${\displaystyle \pi _{2}}$ 映到 ${\displaystyle X\times _{Z}Y}$。

• 這個例子啟發另一種方式考慮拉回：作為態射 ${\displaystyle f\circ p_{1}}$, ${\displaystyle g\circ p_{2}:X\times Y\rightarrow Z}$ 的等化子，這裡${\displaystyle X\times Y}$是 ${\displaystyle X}$ 和 ${\displaystyle Y}$的二元積

而 ${\displaystyle p_{1}}$與 ${\displaystyle p_{2}}$是自然投影。這說明拉回在任何具有二元積和等化子的範疇中存在。事實上，由極限存在定理，在具有有終對象、二元積和等化子的範疇中所有有限極限存在。

拉回的另一個例子來自纖維叢理論：給定一個纖維映射 ${\displaystyle \pi :E\rightarrow B}$ 以及一個連續映射 ${\displaystyle f:X\rightarrow B}$，拉回 ${\displaystyle X\times _{B}E}$ 是 ${\displaystyle X}$ 上的纖維叢，稱為拉回叢。伴隨的交換圖表是纖維叢映射。

在任何具有終對象Z的範疇中，拉回 ${\displaystyle X\times _{Z}Y}$ 恰好是普通積 ${\displaystyle X\times Y}$。

性質

• 如果 ${\displaystyle X\times _{Z}Y}$ 存在，那麼 ${\displaystyle Y\times _{Z}X}$ 也存在，且存在態射 ${\displaystyle X\times _{Z}Y\cong Y\times _{Z}X}$。
• 單態射在拉回下不變：如果箭頭 ${\displaystyle f}$ 單，那麼它就是箭頭 ${\displaystyle p_{2}}$。例如，在集合範疇中，如果 ${\displaystyle X}$ 是 ${\displaystyle Z}$ 的子集，那麼對任何 ${\displaystyle g:Y\rightarrow Z}$，拉回 ${\displaystyle X\times _{Z}Y}$ 是 ${\displaystyle X}$ 在 ${\displaystyle g}$ 下的逆像。
• 同構態射也不變，因此 ${\displaystyle X\times _{X}Y\cong Y}$ 對任何映射 ${\displaystyle Y\rightarrow X}$ 成立。

又見

• 拉回的範疇對偶稱為推出。
• 微分幾何中的拉回。
• 關係代數中的相等連接。

參考文獻

• Adámek, Jiří, Herrlich, Horst, & Strecker, George E.; (1990). Abstract and Concrete Categories （頁面存檔備份，存於網際網路檔案館） (4.2MB PDF). Originally publ. John Wiley & Sons. ISBN 0-471-60922-6. (now free on-line edition).
• Cohn, Paul M.; Universal Algebra (1981), D.Reidel Publishing, Holland, ISBN 90-277-1213-1 (Originally published in 1965, by Harper & Row).

外部連結

• 有趣的網頁給出了有限集合中拉回的例子，作者為Jocelyn Paine。