組內相關

喺統計學上，組內相關（參見英文：ICC）係用嚟衡量數據集中每一組有幾「內部一致」嘅基準：想像有拃數據，有若干個個案，而呢啲個案可以分做若干組，如果拃數據計出嚟嘅組內相關高，就表示同一組嘅個案嘅數值傾向彼此之間接近；要計組內相關可以有幾條唔同嘅式用。^[1]

詮釋方法

設每個藍點為數據中嘅一個個案，每條俾直線串埋一齊嘅藍點係同一組，而打戙軸反映佢哋喺某變數上嘅數值。

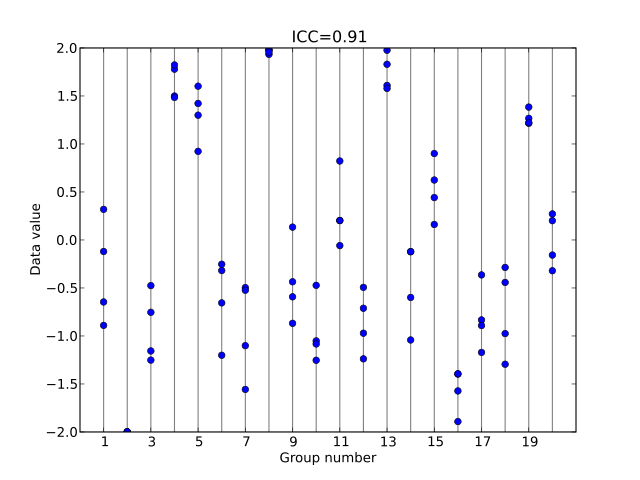
組內相關數值高（接近 1）嘅話，就表示同組個案傾向相似，好似噉（由同一條直線串埋一齊嘅藍點好接近）：

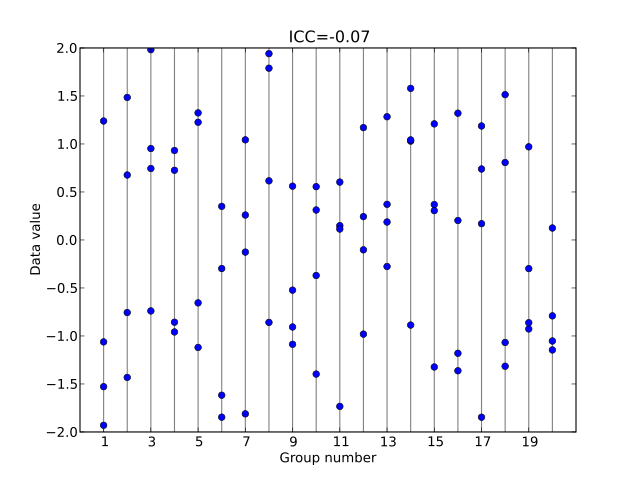
組內相關數值低（接近 0）嘅話，就表示同組個案冇咩特別相似性，好似噉（由同一條直線串埋一齊嘅藍點唔係咁接近）：

現代定義

組內相關嘅現代常用定義係：假設總變異由

• 群組層變異 ${\displaystyle \sigma _{\text{zou2 gaan1}}^{2}}$ 同
• 個體層變異 ${\displaystyle \sigma _{\text{zou2 noi6}}^{2}}$

所組成^[2]，噉組內相關值就等於^[3]：

${\displaystyle \mathrm {ICC} \;=\;{\frac {\sigma _{\text{zou2 gaan1}}^{2}}{\sigma _{\text{zou2 gaan1}}^{2}\;+\;\sigma _{\text{zou2 noi6}}^{2}}}}$

組內相關愈接近 0，就愈表示大部份嘅變異嚟自個體層，群組間冇咩明顯差異；組內相關接近 1，就代表大部份嘅變異嚟自群組層，唔同群組爭好遠。一般嚟講，組內相關愈高，就愈表示需要用多層模型嚟去處理，以正確捕捉群組層面變數嘅影響。

睇埋

• ANOVA
• 統計相關
• 聚類分析
• 多層模型
• 遺傳度