蒙地卡羅方法

蒙地卡羅方法（參見英文：Monte Carlo method）係一柞用隨機性嘅做法嚟應付決定型系統嘅演算法：如果話一個系統係「決定型」嘅，意思係指個系統冇隨機喺裏面，但就算一個系統係決定型嘅，個系統依然有可能會係複雜到難以用決定嘅方法解決^[1]。蒙地卡羅方法源於一九四零年代。

用蒙地卡羅方法迫近常態分佈。

基本概念

用蒙地卡羅方法估計 π 數值嘅圖解；圖上高嘅字，顯示計出嚟個 π 數值同 n（模擬次數）之間嘅關係－n 愈大，計出嚟嘅 π 值就愈接近真嘅圓周率。

睇埋：隨機

蒙地卡羅方法最基本嘅流程如下^[2]：

1. 界定個系統啲輸入嘅可能數值為何（定義域）；
2. 搵個概率分佈（受定義域限制）做輸入數值嘅來源；
3. 用個概率分佈，隨機噉產生一個輸入；
4. 對個輸入做決定型嘅運算；
5. 將步驟 3 同 4 重複 n 咁多次，得到 n 個輸出，再結合數據－例如計嗰 n 個輸出嘅平均值。

舉個簡化例子，想像用蒙地卡羅方法嚟估計圓周率（π）嘅值^[2]：

1. 畫一個正方形，再喺個正方形入面畫個 90° 嘅扇形，任何嘅輸入坐標 (x,y)) 都實會喺個正方形裏面（定義域）；
2. 用個均勻分佈產生一個輸入坐標數值，均勻分佈意思係指每個坐標可能數值出現嘅機率都完全一樣^{[註 1]}；
3. 喺產生出嚟輸入坐標數值嘅位置度畫一點；
4. 將步驟 2 同 3 重複 n 咁多次，然後數吓有幾多點係喺個扇形裏面（同原點距離細過 1）嘅，設呢個數值做 m，如果 n 嘅數值大到接近無限大嘅話，以下呢點會成立：

   ${\displaystyle {\frac {m}{n}}={\frac {\pi }{4}}}$

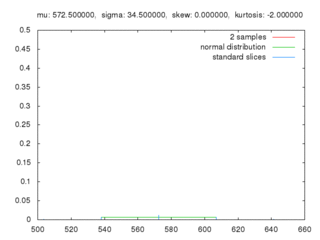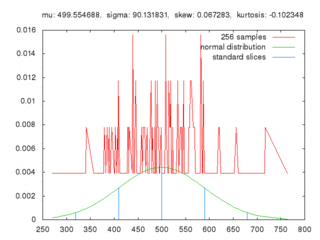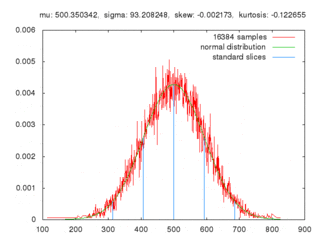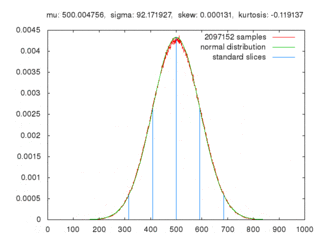
蒙地卡羅方法係用緊「隨機抽樣」嚟嘗試得到近似值：研究者想模擬嗰個系統可能係決定型嘅，但呢個系統可能極其複雜，實用上冇辦法用決定型嘅方式嚟計數；於是研究者就用蒙地卡羅方法。

領域應用

應用統計

睇埋：統計學

遊戲 AI

睇埋：蒙地卡羅樹搜尋

電腦圖像

睇埋

• 複雜系統
• 蒙地卡羅

註釋

1. 睇埋隨機數生成。