متعدد وجوه

في الهندسة، متعدد الوجوه^{[عر 1]} هو شكل ثلاثي الأبعاد ذو وجوه مضلعة مسطحة وحروف مستقيمة وزوايا أو رؤوس مدببة. قد يشير مصطلح "متعدد الوجوه" إما إلى شكل مجسّم أو إلى سطحه المحيط. يشيع استخدام مصطلحي متعدد الوجوه المجسّم وسطح متعدد الوجوه للتمييز بين المفهومين. أيضًا، غالبًا ما يُستخدم مصطلح "متعدد الوجوه" للإشارة ضمنًا إلى البنية الكاملة التي يتكوَّن منها متعدد الوجوه المجسّم، وسطحه، ووجوهه، وحروفه، ورؤوسه.

  ميّز عن متعدد أكناف.

أمثلة عن متعددات الوجوه

رباعي وجوه (مجسم أفلاطوني) اثنا عشري وجوه مُستنجَم صغير  [لغات أخرى]‏ (متعدد وجوه كبلر وبوانسو) ذو وجوه اثنا عشري عشروني (مجسم أرخميدي) مُوَازي وجوه مكعبي مكعبي ثماني عظيم[الإنجليزية] (متعدد وجوه نجمي محتتن[الإنجليزية]) ثلاثوني وجوه معينية  [لغات أخرى]‏ (مجسم كاتالان) متعدد وجوه طاراني[الإنجليزية]
التعريف	مثال ثلاثي الأبعاد لمتعدد أكناف الأكثر عمومية في أي عدد من الأبعاد.
الخواص	عدد الوجوه، التصنيف الطبولوجي ومميزة أويلر، الثنوية، أشكال الرؤوس، مساحة السطح والحجم، الخطوط كما في الخطوط المتقاصرة والأقطار، لامتغير دين، عالي التناظر.
ع ن ت

لمتعدد الوجوه تعريفاتٌ عديدة. ومع ذلك، يُفهم متعدد الوجوه عادةً على أنه تعميم لمضلع ثنائي الأبعاد وتخصيص ثلاثي الأبعاد لمتعدد الأكناف، وهو مفهوم أكثر عمومية في أي عدد من الأبعاد. لمتعدد الوجوه العديد من الخصائص العامة التي تشمل عدد الوجوه، والتصنيف الطبولوجي حسب مميزة أويلر، والثِّنْوِيَّة، وأشكال الرؤوس، ومساحة السطح، والحجم، والخطوط الداخلية، ولامتغير دين، والتناظر. ويعني تناظر متعدد الوجوه أن مظهر متعدد الوجوه لا يتغير بالتحويل مثل الدوران والانعكاس.

يُعرَّف متعدد الوجوه المحدب تعريفًا جيدًا بعدة تعريفات معيارية متكافئة، أحدها هو متعدد الوجوه الذي هو مجموعة محدبة، أو سطح متعدد الوجوه الذي يحده. كل متعدد الوجوه المحدب هو غلاف محدب لرؤوسه، والغلاف المحدب لمجموعة منتهية من النقاط هو متعدد الوجوه. يوجد العديد من عائلات متعددات الوجوه المحدبة، وأكثر الأمثلة شيوعًا هي المكعبات وعائلة الأهرام.

التسمية

يُسمى متعدد الوجوه أيضًا متعدد الأوجه^{[عر 2]} أو كثير الوجوه أو متعدد السطوح^{[عر 3]} أو كثير السطوح^{[عر 4]} أو المجسم^{[عر 5]} مع أن الأخيرة يقصد بها عمومًا منطقة من الفضاء ثلاثي الأبعاد محاطة بسطحٍ مغلقٍ ثنائي الأبعاد؛ وبخصوص مفهومَي الوجه والسطح، فالأول هو شكل مُسطَّح مُضلَّع يُشكِّل جزء من المحيط الخارجي لمتعدد الوجوه، في حين أن الثاني هو في الحقيقة كامل المحيط الخارجي، شاملًا جميع وجوه المتعدد.^{[عر 6]}

أما عن الاسم الإنجليزي polyhedron، فقد أتى من اليونانية (πολύεδρον)، وفيها يعني المقطع πολύ (poly) «كثير» ويعني المقطع ἕδρον (hedron) «قاعدة» أو «جانب شكل مُجسَّم».^[1]

التعريف

يُميَّز عند تعريف متعددات الوجوه بين المحدَّبة منها وتلك التي لا يشترط أن تكون محدبة، فالأولى لها تعريف دقيق يمكن التعبير عنه بعدد من الصيغ المعيارية المكافئة. أما الأخرى، فما زال تعريفها المُعمَّم إشكاليًا، فقد اقترحت مجموعة من التعاريف الشكلية متفاوتة الدقة لوصفها، لكن لم يُعمَّم أي منها وبقيت مقصورة على سياقات مُحدَّدة.^[2] تستبعد بعض هذه التعاريف أشكالًا، غالبًا ما تُعدّ متعددات الوجوه، مثل متعددات الوجوه ذاتية التقاطع^{[الإنجليزية]}، أو تتضمن أشكالًا، لا تُعدّ غالبًا متعددات وجوه صحيحة، مثل المجسمات التي لا تكون حدودها متنوعاتٍ. كما لاحظ برانكو غرونباوم^{[الإنجليزية]}:^[3][ا]

"يُمكِن تتبع أصل مشكلة نظرية متعددات الوجوه وصولًا إلى إقليدس، ومرورًا بكتّاب مثل كبلر وبوانسو وكوشي والكثيرين غيرهم... كلهم أخفقوا، على اختلاف عصورهم، في تحديد ماهية متعددات الوجوه".

يوجد، مع ذلك، اتفاق عام على أن متعدد الوجوه مجسّمٌ أو سطح يمكن وصفه برؤوسه، وهي نقاط زاويّة، وحروفه، وهي قطع مستقيمة تربط بين أزواج معينة من الرؤوس، ووجوهه، وهي مضلعات ثنائية الأبعاد، ويُقبل في بعض الأحيان أن له حجمًا داخليًا معينًا ثلاثي الأبعاد. يمكن التمييز بين هذه التعريفات المختلفة وفقًا لطريقة وصفها لمتعدد الوجوه: مجسم، أو سطح، أو اعتمادًا على خصائصه المجرَّدة التي تحددها هندسة الوقوع^{[الإنجليزية]}.^[4]

• لمتعدد الوجوه تعريف شائع وبسيط: مجسَّم يمكن تغطية حدوده بعدد محدود من المُستوِيات،^[5]، ويمكن صياغة العبارة السابقة بأسلوب آخر: مجسَّم يتكوَّن من اتحاد عدد منتهٍ من متعددات الوجوه المحدَّبة.^[6] وتتطلب التحسينات الطبيعية لهذا التعريف أن يكون المجسَّم محدودًا، وأن يكون له جزء داخلي مترابط، وربما يكون له أيضًا حدود مترابطة. يمكن تعريف وجوه مثل متعدد الوجوه هذا على أنها المُرَكِّبات المترابطة لأجزاء الحدود داخل كل مستوٍ من المستويات التي تغطيه، والحروف والرؤوس على أنها القطع المستقيمة والنقاط التي تلتقي عندها الوجوه. لكن، لا تتضمَّن متعدِّدات الوجوه المُعرَّفة بهذه الطريقة متعدِّدات الوجوه النجمية ذاتية التقاطع، التي قد لا تُشكِّل وجوهها مضلعات بسيطة، وقد تنتمي بعض حروفها إلى أكثر من وجهين.^[7]
• التعريفات القائمة على فكرة السطح المحيط بدلًا من المجسم شائعة أيضًا.^[8] على سبيل المثال، يعرّف أورورك متعدد الوجوه مجموعة وجوه ناتجة عن اتحاد مضلعات محدبة مُرتّبة في الفضاء ترتيبًا يجعل تقاطع أي مضلعين من المجموعة: رأسًا مشتركًا أو حرفًا مشتركًا أو مجموعةً فارغةً مشتركةً، ويجعل اتحادهما متنوعةً.^[9] إذا كان الجزء المستوي من هذا السطح ليس مضلعًا محدبًا في حد ذاته، فإن أورورك يشترط إمكانية تقسيمها إلى مضلعات محدبة أصغر، مع زوايا ثنائية وجوه مسطحة بينها. يُعرِّف غرونباوم متعدد الوجوه غير ذاتي التقاطع، مُعمِّمًا ما سبق كما يأتي: جماعة من المضلعات البسيطة التي تُشكِّل متنوعةً مطمورةً، يقع كل رأس من رؤوسهاعلى ثلاثة أحرف على الأقل، ويتقاطع كل وجهين فقط في رؤوس وحروف مشتركة لكل منهما.^[10] يُعرِّف كرومويل متعددات الوجوه في كتابه^{[الإنجليزية]} تعريفًا مشابهًا لكن دون قيد وجود ثلاثة أحرف على الأقل لكل رأس. ومرة أخرى، لا يشمل هذا النوع من التعريفات متعددات الوجوه ذاتية التقاطع.^[8] تشكِّل المفاهيم المماثلة أساس التعريفات الطبولوجية لمتعدِّدات الوجوه باعتبارها تقسيمات فرعية لمتنوعة طبولوجية إلى أقراص طبولوجية (الوجوه) التي يُشترط أن تكون تقاطعاتها الزوجية نقاطًا (رؤوسًا) أو أقواسًا طبولوجية (حروفًا) أو المجموعة الخالية. ومع ذلك، توجد متعددات الوجوه الطبولوجية (حتى مع جميع الوجوه مثلثة) التي لا يمكن تحقيقها على هيئة متعددات الوجوه غير ذاتية التقاطع.^[11]

الهرم المربع ومتعدد الأكناف المجرد المرتبط به. هنا، يمكن تعريف عناصر الهرم المربع على أنها مجموعة مرتبة جزئيًّا.

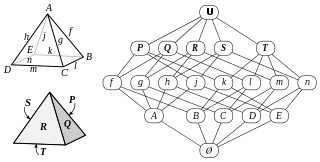
• تعتمد إحدى المقاربات الحديثة على نظرية متعددات الوجوه المجردة^{[الإنجليزية]} التي تُعرِّف متعددات الوجوه بأنها مجموعات مرتبة جزئيًا عناصرها رؤوس المتعدد وحروفه ووجوهه. يكون عنصر الرأس ذا ترتيب جزئي أقل من عنصر الحرف عندما يكون الرأس جزءًا من الحرف، وهذا صحيح لوصف العلاقة بين عنصري الحرف والوجه أيضًا. بالإضافة إلى ذلك، يمكن تضمين عنصر سفلي خاص من هذا الترتيب الجزئي (يمثل المجموعة الفارغة) وعنصر علوي يمثل متعدد الوجوه بأكمله. إذا كانت مقاطع الترتيب الجزئي بين العناصر التي تفصل بينها ثلاثة مُستَوَيات (أي بين كل وجه والعنصر السفلي، وبين العنصر العلوي وكل رأس) لها نفس بنية التمثيل المجرد للمضلع، فإن هذه المجموعات المرتبة جزئيًا تحمل نفس المعلومات التي يحملها متعدد الوجوه الطبولوجي.^{[بحاجة لمصدر]} ومع ذلك، غالبًا ما تُخفَّف هذه المتطلبات، بحيث لا يُشترط سوى أن تكون المقاطع بين العناصر التي تفصل بينها مُستَوَيان متماثلان في البنية مثل التمثيل المجرد لقطعة مستقيمة^[12] (وهذا يعني أن كل حرف يحتوي على رأسين وينتمي إلى وجهين، وأن كل رأس على وجه ينتمي إلى حرفين من ذلك الوجه). يمكن وصف متعددات الوجوه الهندسية المُعرَّفة بطرق أخرى وصفًا تجريديًّا بهذه الطريقة، ولكن من الممكن أيضًا استخدام متعدِّدات الوجوه المجرَّدة لأنها أساس لتعريف متعدِّدات الوجوه الهندسية. عادةً ما يُعتبَر "تحقيق" متعدِّد الوجوه المجرَّد بمثابة تطبيق من رؤوس متعدِّد الوجوه المجرَّد إلى نقاط هندسية، بحيث تكون نقاط كل وجه في نفس المستوي. يمكن عندئذٍ تعريف متعدد الوجوه الهندسي على أنه تحقيق لمتعدد الوجوه المجرَّد.^[13] كما أُخِذت بعين الاعتبار عمليات التحقيق التي تحذف شرط استواء الوجه، أو تفرض متطلبات إضافية للتناظر، أو التي تُقْرِن الرؤوس بأفضية ذات أبعاد أعلى.^[12] على عكس التعريفات القائمة على المجسّم والسطح، يعمل هذا جيدًا تمامًا مع متعددات الوجوه النجمية. لكن، من دون قيود إضافية، يسمح هذا التعريف بوجود متعددات وجوه منحلة أو غير أمينة (على سبيل المثال، عن طريق تطبيق جميع الرؤوس إلى نقطة واحدة)، ولم تُحْسَم مسألة كيفية تقييد التحقيقات لتجنب هذه الانحلالات.

يُفهم عادةً، من التعريفات السابقة، أن متعدد الوجوه مثال ثلاثي الأبعاد لمتعدد الأكناف. مثلًا، للمضلع جسم ثنائي الأبعاد وليس له أي وجه، في حين أن لمتعدد الأكناف رباعي الأبعاد جسم رباعي الأبعاد ومجموعة إضافية من "الخلايا" ثلاثية الأبعاد. بخلاف ذلك، يُستخدَم مصطلح "متعدد الوجوه" في بعض أدبيات الهندسة الرياضية ذات الأبعاد العليا لوصف شيء مختلف عن متعدد الأكناف ثلاثي الأبعاد، ومختلف عن متعدد الأكناف بطريقة ما. تُعرِّف بعض المصادر، على سبيل المثال، متعدد الوجوه المحدَّب بأنه تقاطع عدد محدود من أنصاف الأفضية^{[الإنجليزية]}، ومتعدد الأكناف بأنه متعدد وجوه محدود.^[14][15] تقتصر هذه المقالة على تناول متعددات الوجوه ثلاثية الأبعاد.

المميزات العامة

التصنيف الطبولوجي

المقالة الرئيسة: متعدد وجوه طاراني^{[الإنجليزية]} ومميزة أويلر

مُوَازي الوجوه الرباعي نصف السداسي^{[الإنجليزية]}، وهو متعدد وجوه ذاتي التقاطع غير قابل للتوجيه له أربعة أوجه مثلثة (أحمر) وثلاثة أوجه مربعة (أصفر). كما هو الحال مع شريط موبيوس أو قارورة كلاين، يمكن أن يصل مسار مستمر على طول سطح متعدد الوجوه هذا إلى نقطة على الجانب المقابل للسطح من نقطة البداية، مما يجعل من المستحيل فصل السطح إلى داخل وخارج. (من الناحية الطبولوجية، متعدد الوجوه هذا هو مستوٍ إسقاطي حقيقي^{[الإنجليزية]}).

بعض متعددات الوجوه لها جانبان مختلفان لسطحها. على سبيل المثال، يمكن إعطاء كلٍ من الجزء الداخلي والخارجي لنموذج ورقي لمتعدد الوجوه المحدب بلون مختلف (على الرغم من أن اللون الداخلي سيكون مخفيًا عن الأنظار). متعددات الوجوه هذه قابلة للتوجيه^{[الإنجليزية]}. وينطبق الأمر نفسه على متعددات الوجوه غير المحدبة التي لا تحتوي على تقاطعات ذاتية. يمكن تلوين بعض متعددات الوجوه غير المحدبة غير ذاتية التقاطع بالطريقة نفسها ولكن بها مناطق مقلوبة "من الداخل إلى الخارج" بحيث يظهر كلا اللونين من الخارج في أماكن مختلفة؛ وهذه لا تزال تعتبر قابلةً للتوجيه. ومع ذلك، بالنسبة لبعض متعددات الوجوه الأخرى ذاتية التقاطع ذات الوجوه المضلعة البسيطة مثل مُوَازي الوجوه الرباعي نصف السداسي^{[الإنجليزية]} لا يمكن تلوين جانبي كل وجه بلونين مختلفين بحيث يكون للوجهين المتجاورين ألوان متناسقة. في هذه الحالة يُقال إن متعدد الوجوه غير قابل للتوجيه. قد لا يكون من الواضح ما يعنيه أن تكون الوجوه المتجاورة ملونة تلوينًا متناسقًا بالنسبة إلى متعددات الوجوه ذات الوجوه المتقاطعة ذاتيًّا، لكن بالنسبة إلى هذه المتعددات يظل من الممكن تحديد ما إذا كانت قابلة للتوجيه أو غير قابلة للتوجيه لأن مُجمَّع خلوي^{[الإنجليزية]} طبولوجي له الوقوعات نفسها بين رؤوسها وحروفها ووجوهها.^[16]

يمكن اعتماد مميزة أويلر للتمييز بدقة بين سطوح متعددات الوجوه، تضم صيغتها أعداد رؤوس متعدد الوجوه ${\displaystyle V}$ وحروفه ${\displaystyle E}$ ووجوهه ${\displaystyle F}$، وهي ترتبط بعضها مع بعض لإنتاج العدد ${\displaystyle \chi }$ كما يأتي:

${\displaystyle \chi =V-E+F\ }$

تُستخدم صيغة مميزة أويلر نفسها أيضًا لأنواع أخرى من السطوح الطبولوجية. وهي من لامتغيرات السطح، ما يعني أنه عند تقسيم السطح الواحد إلى رؤوس وحروف ووجوه بأكثر من طريقة، تكون مميزة أويلر هي نفسها لهذه التقسيمات الجزئية. بالنسبة إلى متعدد الوجوه المحدب، أو بشكل أعم أي متعدد وجوه بسيط الارتباط له سطح كرة طبولوجية، فإن مميزته تساوي دائمًا 2. بالنسبة إلى الأشكال الأكثر تعقيدًا، ترتبط خاصية أويلر بعدد الثقوب أو المقابض أو القبعات المتصالبة شبه الطارية في السطح وتكون أقل من 2.^[17] جميع متعددات الوجوه ذات مميزات أويلر فردية العدد غير قابلة للتوجيه. قد يكون الشكل المعطى ذو مميزة أويلر زوجية قابلًا للتوجيه أو غير قابل للتوجيه. على سبيل المثال، الطاراني وحيد الثقب وقارورة كلاين لهما ${\displaystyle \chi =0}$، حيث يكون الأول قابلًا للتوجيه والأخرى غير قابلة للتوجيه.^[16]

يلزم، في العديد من طرق تعريف متعدد الوجوه، أن يكون سطحه متنوعةً، ولكن هذا ليس شرطًا لازمًا في التعاريف كلها. يعني أن يكون سطح متعدد الوجوه متنوعةً أن كل حرف هو جزء من حدود وجهين بالضبط، ولا يُسمَح بأشكال مثل اتحاد مكعبين يلتقيان فقط على طول حرف مشترك، وأن كل رأس يتقاطع مع دورة واحدة متناوبة من الحروف والوجوه، أي لا يُسمَح بأشكال مثل اتحاد مكعبين يشتركان في رأس واحد فقط. إن تصنيف المتنوعات^{[الإنجليزية]} لمتعددات الوجوه المُعرَّفة بهذه الطرق، يعني أن النمط الطبولوجي للسطح يتحدد تمامًا من خلال الجمع بين خاصية أويلر وقابلية للتوجيه. على سبيل المثال، لو كان سطح أي متعدد وجوه متنوعةً قابلةً للتوجيه وكانت مميزة أويلر له مساوية 2، فيلزم أن يكون كرة طبولوجية.^[16]

متعدد الوجوه الطاراني^{[الإنجليزية]} متعدد وجوه مميزة أويلر فيه أقل من 0 أو مساوية لها، أو ما يعادل جنسه^{[الإنجليزية]} 1 أو أكثر. من الناحية الطبولوجية، سطوح مثل متعددات الوجوه هذه هي سطوح طارية بها ثقب واحد أو أكثر في المنتصف.^[18] أحد الأمثلة البارزة على ذلك هو متعدد وجوه سيلاشي^{[الإنجليزية]}، الذي ينجز تطبيق هيوود^{[الإنجليزية]} هندسيًا.

الثِّنْوِيَّة

المقالة الرئيسة: متعدد وجوه ثنوي

ثماني الوجوه ثنوي للمكعب

لكل متعددِ وجوهٍ مُحدَّب متعددُ وجوهٍ ثِنْوِيٌّ له:

• وجوه بدلًا من رؤوس الأصل.
• رؤوس بدلًا من وجوه الأصل.
• عدد حروف الأصل نفسها.

يمكن الحصول على ثنوي متعدد الوجوه المحدب عن طريق عملية التحويل المعاكس القطبي.^[19] توجد متعدِّدات الوجوه الثنوية في أزواج، وثنوي الثنوي هو متعدد الوجوه الأصل نفسه. بعض مُتعدِّدات الوجوه تكون ثنوية ذاتيًّا، ما يعني أن ثنوي مُتعدِّد الوجوه يكون مطابقًا لمتعدد الوجوه الأصلي.^[20]

متعددات الوجوه المجردة لها أيضًا ثنويات، يُحصَل عليها عن طريق عكس الترتيب الجزئي التي يُعرِّف متعدد الوجوه للحصول على رتبته الثنوية أو رتبته المعاكسة^{[الإنجليزية]}.^[13] وهذه لها نفس مميزة أويلر وقابلية التوجيه مثل متعدد الوجوه الابتدائي. ومع ذلك، لا يصف شكل الثنوية هذا هيئة متعدد الوجوه الثنوي، بل يصف فقط بنيته التوافيقية. بالنسبة لبعض تعريفات متعددات الوجوه الهندسية غير المحدبة، توجد متعددات وجوه لا يمكن تحقيق ثنوياتها المجردة على شكل متعددات وجوه هندسية بموجب التعريف نفسه.^[10]

أشكال الرؤوس

المقالة الرئيسة: شكل رأس

من أجل كل رأس، يمكن تعريف شكل الرأس الذي يصف البنية المحلية لمتعدد الوجوه حول الرأس. تختلف التعاريف الدقيقة، لكن يمكن اعتبار شكل الرأس على أنه المضلع المكشوف الناتج عن قطع شريحة عبر متعدد الوجوه لأحد الرؤوس.^[8] بالنسبة للمجسمات الأفلاطونية ومتعددات الوجوه الأخرى عالية التناظر، يمكن اختيار هذه الشريحة لتمر عبر نقاط منتصف كل حرف واقع على الرأس،^[21] لكن قد لا يكون لمتعددات الوجوه الأخرى مستوٍ يمر عبر هذه النقاط. بالنسبة إلى متعددات الوجوه المحدبة، وبشكل أعم بالنسبة إلى متعددات الوجوه التي تكون رؤوسها في وضع مُحدَّب، يمكن اختيار هذه الشريحة باعتبارها مستويًا يفصل الرأس عن الرؤوس الأخرى.^[22] عندما يكون لمتعدد الوجوه مركز تناظر، فمن المعتاد اختيار هذا المستوي ليكون عموديًا على الخط المار بالرأس المعطى والمركز؛^[23] وبهذا الاختيار، تتحدد هيئة شكل الرأس وتبقى محددةً حتى بضبط الأبعاد. عندما لا تكون رؤوس متعدد الوجوه في وضع محدب، لن يكون هناك دائمًا مستوٍ يفصل كل رأس عن بقية الرؤوس. في هذه الحالة، من الشائع بدلًا من ذلك تشريح متعدد الوجوه بِكُرَة صغيرة مركزها عند الرأس.^[24] مرة أخرى، يُنتِج هذا هيئةً لشكل الرأس ثابتةً حتى بضبط الأبعاد. جميع هذه الخيارات تُؤدي إلى أشكال رأس ذات نفس البنية التوافيقية لمتعددات الوجوه التي يُمكن تطبيقها عليها، ولكنها قد تُعطيها هيئاتٍ هندسية مختلفة.

مساحة السطح والخطوط داخل متعددات الوجوه

مساحة سطح متعدِّد الوجوه هي مجموع مساحات وجوهه، وذلك من أجل تعريفات متعدِّدات الوجوه التي تكون مساحة الوجه فيها مُعرَّفة جيدًا. تقيس المسافة المتقاصرة بين أي نقطتين على سطح متعدد الوجوه طول أقصر منحنٍ يصل بين النقطتين، ويبقى داخل السطح. وفقًا لمبرهنة ألكسندروف للوحدانية^{[الإنجليزية]}، يُحدَّد كل متعدد وجوه محدَّب بالفضاء المتري للمسافات المتقاصرة على سطحه تحديدًا فريدًا. ولكن هذا لا ينطبق على متعدِّدات الوجوه غير المحدَّبة، فقد تتساوى مسافات السطح لدى بعضها مع بعض آخر، وقد تتساوى مسافات سطح بعضها مع تلك الخاصة بمتعددات وجوه محدَّبة.^[25]

عندما تربط القطع المستقيمة بين رأسين لا يقعان في الوجه نفسه، فإنها تشكِّل أقطارًا.^[26] ومع ذلك، لا تحتوي جميع متعددات الوجوه على مستقيمات قطرية، كما هو الحال في عائلة الأهرام،^{[بحاجة لمصدر]} ومتعدد وجوه شونهارت^{[الإنجليزية]} الذي يحتوي على ثلاثة مستقيمات قطرية تقع خارجها بالكامل، ومتعدد وجوه تشاسار^{[الإنجليزية]} لا تحوي مستقيمات قطرية (بل كل زوج من الرؤوس متصل بحرف).^[27]

الحجم

للمجسمات المتعددة الوجوه كمية مرتبطة بها تسمى الحجم تقيس مقدار الفضاء الذي تشغله. قد يكون لعائلات المجسمات البسيطة صيغ بسيطة لحجومها؛ على سبيل المثال، يمكن التعبير بسهولة عن أحجام الأهرام والمواشير ومتوازيات الوجوه بدلالة أطوال حروفها أو الإحداثيات الأخرى.

قد لا يكون لأحجام متعددات الوجوه الأكثر تعقيدًا صيغ بسيطة. يمكن حساب حجم مُتعدِّدات الوجوه منها عن طريق تقسيمه إلى أجزاء أصغر، بالتثليث الزاوي مثلًا. يُحسَب حجم المجسَّم الأفلاطوني، على سبيل المثال، بتقسيمه إلى أهرام متطابقة تكون قاعدة كل منها وجه من متعدد الوجوه وفي حين يكون مركز متعدد الوجوه قمة لها كلها.

يمكن انطلاقًا من مبرهنة التباعد استنتاج أن حجم المجسَّم متعدد الوجوه يُعطى بالعلاقة التالية: $${\displaystyle {\frac {1}{3}}\left|\sum _{F}(Q_{F}\cdot N_{F})\operatorname {area} (F)\right|}$$وفيها يُمثِّل ${\displaystyle F}$ وجوه المُتعدِّد، و${\displaystyle Q_{F}}$ نقطة كيفية على الوجه ${\displaystyle F}$، و${\displaystyle N_{F}}$ متجه الوحدة العمودي على الوجه ${\displaystyle F}$ والذي يشير إلى خارج المجسَّم، ويشير مُؤثِّر النقطة إلى عملية الجداء السُلَّمي.^[28] قد يكون حساب الحجم صعبًا في الأبعاد الأعلى، ويرجع ذلك جزئيًّا إلى صعوبة سرد وجوه المتعدد المحدّب المحدّد برؤوسه فقط، وتوجد خوارزميات مخصصة لتحديد الحجم في هذه الحالات.^[29]

لامتغير دين

المقالة الرئيسة: لامتغير دين

تؤكد مبرهنة بوياي وغيرفين على إمكانية تحويل أي مضلع إلى آخر له المساحة نفسها بتقطيعه إلى عدد غير منتهٍ من أجزاء المضلع ثم إعادة ترتيبها في فضاء ثنائي الأبعاد. كان السؤال المماثل لمتعددات الوجوه هو موضوع مسألة هلبرت الثالثة^{[الإنجليزية]}. حلّ ماكس دين هذه المسألة بإظهار أنه، على عكس حالة ثنائي الأبعاد، توجد متعددات الوجوه من نفس الحجم لا يمكن تقطيعها إلى متعددات وجوه أصغر وإعادة تجميعها مع بعضها البعض. ولإثبات ذلك اكتشف دين قيمة أخرى مرتبطة بمتعدد الوجوه، وهي لامتغير دين، بحيث لا يمكن تقطيع متعددَي الوجوه إلى بعضهما البعض إلا إذا كان لهما الحجم نفسه ولامتغير دين نفسه. وقد أثبت سيدلر^{[الإنجليزية]} لاحقًا أن هذه هي العقبة الوحيدة أمام التقطيع: يمكن تقطيع كل متعددَي الوجوه الإقليديين بنفس الأحجام ولامتغيرات دين وإعادة تجميعهما بعضهما في بعض.^{[فر 1]} لامتغير دين ليس عددًا، بل متجه في فضاء متجهي لانهائي الأبعاد، يُحدَّد من أطوال وزوايا ثنائية الوجوه لحروف متعدد الوجوه.^{[وب-إنج 1]}

تتناول مسألة هلبرت الثامنة عشر^{[الإنجليزية]}، فيما تتناوله، متعددات الوجوه المُبطلِّة الفضاء. يلزم أن تكون قيمة له لامتغير دين لأي متعدد الوجوه من هذا النوع مساوية للصفر.^{[ألم 1]} كما يُربَط لامتغير دين بمتعدد الوجوه الانثنائي^{[الإنجليزية]} بمبرهنة الكِّير القوي التي تنص على أن لامتغير دين لأي متعدد وجوه انثنائي يبقى غير متغير أثناء انثناءه.^[30]

التناظرات

بعض متعددات الوجوه التي تدور حول محاور تناظرها (في مجموعة ماتيماتيكا لمعهد الرياضيات والإحصاء لجامعة ساو باولو^{[الإنجليزية]})

العديد من متعددات الوجوه الأكثر دراسةً عالية التناظر. لا يتغيّر مظهرها بفعل الانعكاسات على المستوي أو الدوران حول المحاور التي تمر عبر رأسين أو حرفين أو وجهين متقابلين في الفضاء. قد يغيّر كل تناظر موقع عنصر معين، لكن مجموعة كل الرؤوس (وكذلك الوجوه والحروف) لا تتغير. تُسمَّى جماعة تناظرات متعدد الوجوه زمرة التناظر الخاصة به.^[31]

حسب عناصر متعدد وجوه

يُقال إن عناصر متعدد الوجوه: الرأس والوجه والحرف، التي تتراكب بعضها على بعض بفعل التناظرات، تُشكِّل مدار تناظر. إذا كانت هذه العناصر تقع في المدار نفسه، فقد يكون الشكل انتقاليًا على المدار. كلٌّ منها على حدة متساوي الوجوه^{[الإنجليزية]} (أو انتقالي الوجوه، ما يعني أن تحويلات التناظر تتضمن وجوه المتعددات في المدار)،^[32][ب] ومتساوي الحروف^{[الإنجليزية]} (أو انتقالي الحروف، أي يتضمن حروف متعددات الوجوه)،^[33] ومتساوي الرؤوس^{[الإنجليزية]} (أو انتقالي الرؤوس، أي يتضمن رؤوس متعددات الوجوه). على سبيل المثال، المكعب الذي تكون فيه جميع الوجوه في مدار واحد ويتضمن الدوران والانعكاسات في المدار يبقى دون تغيير في مظهره؛ ومن ثم، يكون المكعب انتقالي الوجوه. يحتوي المكعب أيضًا على التناظرين الآخرين من هذا القبيل.^[34]

عندما تنتمي ثلاثة من هذه التناظرات إلى مُتعدِّد الوجوه، يُعرَف بمتعدد الوجوه المنتظم.^[34] توجد تسعة متُعدِّدات الوجوه المنتظمة: خمسة مجسمات أفلاطونية (مكعب، وثماني الوجوه، وعشروني الوجوه، ورباعي الوجوه، واثنعشري الوجوه، وجميعها ذات وجوه مضلعة منتظمة) وأربعة متعددات وجوه كبلر وبوانسو. ومع ذلك، قد لا تمتلك بعض مُتعدِّدات الوجوه واحدًا أو اثنين من هذه التناظرات:

المكعب متعدد وجوه منتظم، لأن وجوهه وحروفه ورؤوسه انتقالية إلى أخرى، ومظهره لم يتغير.

• يُقال عن متعدد الوجوه انتقالي الرؤوس والحروف أنه شبه منتظم^{[الإنجليزية]}، مع أن له وجوهًا منتظمة، وثنويه انتقالي الوجوه والحروف.
• يُقال عن متعدد الوجوه انتقالي الرؤوس وغير انتقالي الحروف ذو الوجوه المضلعة المنتظمة أنه نصف منتظم^{[الإنجليزية]}،^[ج] ومثل متعددات الوجوه هذه هي الموشورات والموشورات التخالفية. وثنويها انتقالي الوجوه وليس انتقالي الرؤوس، وكل رأس منتظم.
• يُقال عن متعدد الوجوه انتقالي الرؤوس ذي الوجوه المضلعة المنتظمة أنه مُحتَتِن. قد ينقسم هذا الصنف إلى متعدد الوجوه المنتظم أو شبه المنتظم أو نصف المنتظم، وقد يكون محدبًا أو نجميًا. يكون الثنوي انتقالي الوجوه وله رؤوس منتظمة، لكنه ليس بالضرورة انتقالي الرؤوس. عادةً ما تُصنَّف مُتعدِّدات الوجوه المحتتنة وثنوياتها تقليديًا وفقًا لدرجة تناظرها، وما إذا كانت محدَّبة أم لا.
• يُقال عن متعدد الوجوه الانتقالي الوجوه والرؤوس (ولكن ليس بالضرورة انتقالي الحروف) أنه نبيل^{[الإنجليزية]}. متعددات الوجوه المنتظمة نبيلة أيضًا؛ فهي متعددات الوجوه المحتتنة النبيلة الوحيدة. ثنويات متعددات الوجوه النبيلة هي نفسها نبيلة.

قد لا يكون لبعض متعددات الوجوه تناظر انعكاسي بحيث يكون لها شكلان متخايلان، وهما انعكاسان لبعضهما البعض. ويُعرف هذا التناظر بامتلاكه لليدوانية. وتشمل الأمثلة على ذلك ذا الوجوه المكعبي الثماني الأفطس وذا الوجوه الاثنعشري العشروني الأفطس^{[الإنجليزية]}.

حسب الزمرة النقطية في ثلاثي الأبعاد

المقالة الرئيسة: زمر نقطية في الأبعاد الثلاثة^{[الإنجليزية]}

يمتلك رباعي الوجوه المنتظم تناظر رباعي وجوه كامل: دوران ثلاثي حول المحور يمر عبر كل من الرأس والوجه المثلث، ودوران ثنائي حول المحور عبر حرفين، وكذلك مستوي الانعكاس عبر وجهين وحرف واحد

للهرم المربع تناظر هرمي ${\displaystyle C_{4\mathrm {v} }}$. ويوضِّح أن مظهره ثابت بدوران كل ربع دورة كاملة حول محوره، ويمتلك تناظرًا انعكاسيًّا بالنسبة إلى أي مستوٍ عمودي يمر بمُنصِّف قاعدته

يُقصد بالزمرة النقطية لمتعددات الوجوه^{[الإنجليزية]} زمرة رياضية تتمتع بعمليات التناظر^{[الإنجليزية]} الخاصة بها بحيث يظل مظهر متعددات الوجوه محفوظًا أثناء التحويل في الفضاء الثلاثي الأبعاد. ويشمل التحويل المشار إليه هنا الدوران حول المحاور، والانعكاس على المستوي، والتعاكس عبر نقطة مركزية، وجمع بين هذه الثلاثة.^[35]

زمرة متعدد الوجوه^{[الإنجليزية]} هي زمرة التناظر المشتقة في الأصل من المجسَّمات الأفلاطونية الثلاثة: رباعي الوجوه وثمانيها وعشرونيها. ولهذه الزمر الثلاث زمر نقطية تُعرَف على الترتيب بتناظر رباعي الوجوه^{[الإنجليزية]} وتناظر ثماني الوجوه^{[الإنجليزية]} وتناظر عشروني الوجوه^{[الإنجليزية]}. ويركز كل منها على زمرة دوران متعددات الوجوه التي تُعرَف باسم "زمرة متعدد الوجوه اليدوانية"، في حين أن مجموعة التناظر الانعكاسية الإضافية تُعرَف باسم زمرة متعدد الوجوه الكاملة. تتضمن إحدى الزمر النقطية، وهي التناظر البيريتي^{[الإنجليزية]}، دوران تناظر رباعي الوجوه، بالإضافة إلى ثلاثة مُستوِيات من التناظر الانعكاسي وبعض الانعكاسات الدورانية^{[الإنجليزية]}. وعمومًا، تتلخص زمر متعدد الوجوه المذكورة في النقاط التالية:^[36]

• تناظر رباعي الوجوه اليدواني ${\displaystyle \mathrm {T} }$، وهو زمرة الدوران لرباعي الوجوه المنتظم، ومرتبتها اثنا عشر.
• تناظر رباعي الوجوه الكامل ${\displaystyle \mathrm {T} _{\mathrm {d} }}$، وهو زمرة التناظر لرباعي الوجوه المنتظم، ومرتبتها أربعة وعشرون.
• التناظر البيريتي ${\displaystyle \mathrm {T} _{\mathrm {h} }}$، وهو تناظر بيريتي الوجوه  ^{[لغات أخرى]}‏ وله مرتبة أربعة وعشرين.
• تناظر ثماني الوجوه اليدواني ${\displaystyle \mathrm {O} }$، وهو زمرة الدوران لكلٍّ من المكعب وثماني الوجوه المنتظم، ومرتبته أربعة وعشرون.
• تناظر ثماني الوجوه الكامل ${\displaystyle \mathrm {O} _{\mathrm {h} }}$، وهو زمرة التناظر لكلٍّ من المكعب وثماني الوجوه المنتظم، ومرتبته ثمانية وأربعون.
• تناظر عشروني الوجوه اليدواني ${\displaystyle \mathrm {I} }$، وهو زمرة الدوران لكلٍّ من عشروني الوجوه المنتظم واثنعشري الوجوه المنتظم، ومرتبته ستون.
• تناظر عشروني الوجوه الكامل ${\displaystyle \mathrm {I} _{\mathrm {h} }}$، وهي زمرة التناظر لكلٍّ من عشروني الوجوه المنتظم واثنعشري الوجوه المنتظم، ومرتبته مئة وعشرون.

قد تسمح الزمر النقطية في ثلاثة أبعاد أيضًا بالحفاظ على مظهر متعدد الوجوه من خلال الجريان حول محور ما. توجد ثلاث زمر نقطية مختلفة من هذه الزمر النقطية:

• التناظر الهرمي ${\displaystyle C_{n\mathrm {v} }}$، الذي يسمح بتدوير المحور المار عبر القمة وقاعدتها، وكذلك الانعكاس بالنسبة للمُستوِيات المتعامدة التي تمر بمُنصِّف القاعدة. يمكن إيجاد هذا تناظر الزمرة النقطية في الأهرامات،^[37] والقباب والطوارم.
• التناظر الموشوري ${\displaystyle D_{n\mathrm {h} }}$، على غرار التناظر الهرمي، ولكن مع تحويل إضافي عن طريق عكسه عبر مستوٍ أفقي. يمكن تحقيق ذلك من عائلة الموشورات وثنوياتها ثنائيات الأهرام.^[37]
• التناظر الموشوري التخالفي ${\displaystyle D_{n\mathrm {v} }}$، الذي يحافظ على التناظر من خلال تدوير نصفه السفلي وعكسه عبر المستوي الأفقي.^[37] يمكن إيجاد أمثلة في الموشورات التخالفية.

تتكوَّن الزمرة النقطية ${\displaystyle C_{n\mathrm {h} }}$ من الدوران حول محور التناظر والانعكاس على المستوي الأفقي. في حالة ${\displaystyle n=1}$، فإن زمرة التناظر تحافظ على التناظر فقط من خلال الدوران الكامل فقط، وعادةً ما يُرمز لها بـ ${\displaystyle C_{s}}$.^[38] قد يكون لمتعددات الوجوه دوران فقط للحفاظ على التناظر، ويمكن اعتبار زمرة التناظر هي الزمرة الدورية ${\displaystyle C_{n}}$.^[39] متعددات الوجوه مع الانعكاس الدوراني والدوران بالزمرة الدورية هي الزمرة النقطية ${\displaystyle S_{n}}$.^[40]

متعددات الوجوه المحدبة

من أعلى اليمين إلى أسفل اليسار: الهرم المسدس من عائلة الموشوريات، ورباعي الوجوه المبتور^{[الإنجليزية]} من عائلة المجسمات الأرخميدية، وعشروني الوجوه المثلوثة^{[الإنجليزية]} من عائلة مجسمات كاتالان، والموشور المثلث ثلاثي التعزيز^{[الإنجليزية]} ضمن عائلتَيْ دلتاويات الوجوه ومجسمات جنسون. كل هذه الأصناف متعددات وجوه محدبة.

كما ذُكر أعلاه، متعددات الوجوه المحدَّبة مُعرَّفة تعريفًا جيدًا، مع العديد من التعريفات المعيارية المكافئة. وغالبًا ما تُعرَّف على أنها تقاطعات محدودة لعدد منتهٍ من أنصاف الأفضية^{[الإنجليزية]}،^[14][15] أو على أنها غلاف محدب لعدد منتهٍ من النقاط،^[41] مقتصرة في كلتا الحالتين على التقاطعات أو الأغلفة التي لا يساوي حجمها صفرًا.

تشمل الأصناف المهمة من متعددات الوجوه المحدبة عائلة الموشوريات، والمجسمات الأفلاطونية، والمجسمات الأرخميدية وثنوياتها التي تدعى مجسمات كاتالان، ومتعددات الوجوه المحدبة التي تكون جميع وجوهها مضلعاتٍ منتظمة. الموشوريات هي متعددات الوجوه التي تقع رؤوسها على مستويين متوازيين ووجوهها على الأرجح أشباه منحرف ومثلثات.^[42] ومن الأمثلة على الموشوريات، الأهرام والأسافين ومتوازيات الوجوه والموشورات والموشور التخالفي والقباب والجذوع. أما المجسمات الأفلاطونية فهي متعددات الوجوه الخمسة القديمة - رباعي الوجوه، وثماني الوجوه، وعشروني الوجوه، والمكعب، واثنعشري الوجوه - التي صنفها أفلاطون في حواره "طيماوس" والتي تربط بين العناصر التقليدية الأربعة للطبيعة.^[43] المجسّمات الأرخميدية هي صنف المجسّمات الثلاثة عشر التي تكون جميع وجوهها مضلعات منتظمة وتكون رؤوسها متناظرة مع بعضها البعض؛^[د] ثنوياتها هي مجسمات كاتالان.^[45] مجسّمات جونسون هي صنف من متعددات الوجوه المحدبة التي تكون جميع وجوهها مضلعات منتظمة.^[46] وتشمل هذه دلتاويات الوجوه المحدبة، وهي متعددات وجوه محدبة تمامًا تكون جميع وجوهها مثلثات متساوية الأضلاع.^[47]

يمكن تصنيف متعددات الوجوه المحدبة إلى فئة متعددات الوجوه الابتدائية أو فئة متعددات الوجوه المؤلفة^{[الإنجليزية]}. هي متعددات الوجوه المحدبة المنتظمة الوجوه التي لا يمكن تحويلها إلى مُتعددَيْ وجوه أو أكثر عن طريق تشريحها بمستوٍ.^[48] على النقيض تمامًا من متعددات الوجوه المؤلفة، يمكن تعريفها بدلًا من ذلك بأنها متعددات الوجوه التي أُنشئت عن طريق ربط المزيد من متعددات الوجوه الابتدائية. على سبيل المثال، يعتبر الموشور المثلث ثلاثي التعزيز^{[الإنجليزية]} مؤلفًا لأنه يمكن إنشائه عن طريق ربط ثلاثة أهرام مربعة متساوية الحروف على الوجوه المربعة لموشور مثلث؛ وفيها الأهرام المربعة والموشور المثلث هي متعددات وجوه أولية.^[49]

متعدد وجوه قانوني

هيكل الموشور المثلث ثلاثي التعزيز على هيئة بيان

بعض متعددات الوجوه المحدبة تمتلك كرةً وسيطةً، وهي كرة مُماسّة لكل حروفها، ويكون نصف قطرها وسيطًا بين الكرة المحاطة والكرة المحيطة^{[الإنجليزية]} لمتعدد الوجوه الذي توجد فيه هذه الكرات الثلاث جميعها. كل متعدد الوجوه المحدَّب يكافئ من الناحية التوافيقية "متعدد وجوه قانوني"، وهو متعدد وجوه له كرة وسيطة يتطابق مركزه مع مركزه. تُحدَّد هيئة متعدد الوجوه القانوني (وليس أبعاده أو موضعه) بشكل فريد من خلال البنية التوافيقية لمتعدد الوجوه المُعطى.^[50]

ينتج عن أي متعدد الوجوه، أيًا كانت بنية الوجه، بيانٌ يُسمَّى هيكله^{[الإنجليزية]}، برؤوس وحروف مقابلة له. لهذه الأشكال تاريخ طويل: فقد ابتكر ليوناردو دا فنشي نماذج إطارية للمجسمات المنتظمة، التي رسمها لكتاب بتشولي "النسبة الإلهية"، وتظهر أشكال متعددة الوجوه مماثلة ذات إطار سلكي في لوحة "نجوم^{[الإنجليزية]}" التي رسمها ماوريتس إيشر.^[51] ومن أبرز ما يميز هذه المقاربة مبرهنة شتاينتس^{[الإنجليزية]}، التي تعطي توصيفًا نظريًا بيانيًا بحتًا لهيكل متعدد الوجوه المحدب: فهي تنص على أن هيكل كل متعدد وجوه محدب هو بيان مستوٍ ثلاثي الترابط^{[الإنجليزية]}، وكل بيان من هذا القبيل هو هيكل لبعض متعددات الوجوه المحدبة.^[52]

بيان هِرْشِل^{[الإنجليزية]} هو بيان مستوٍ بيان مترابط كافي الرؤوس^{[الإنجليزية]}، ويستوفي مبرهنة شتاينتس^{[الإنجليزية]}.^{[وب-إنج 2]} وينتج عن ذلك تساعي وجوه رباعية الأضلاع.^[53]

بعض مُتعدِّدات الوجوه لا تتمتع بخاصية التحدُّب، وتُسمَّى مُتعدِّدات الوجوه غير المحدَّبة. وهي متعددات الوجوه النجمية^{[الإنجليزية]} ومتعددات وجوه كبلر وبوانسو التي تُنشأ إما عن طريق الاستنجام أو الوَيْجَهَة. الاستنجام هو عملية تمديد الوجوه (داخل مُستوِياتها) بحيث تلتقي. الويجهة هي عملية إزالة أجزاء من متعدد الوجوه لإنشاء وجوه جديدة (أو وُجَيهات) دون إنشاء أي رؤوس جديدة.^[54][55] وُجَيه متعدد وجوه هو أي مضلع تكون زواياه رؤوسًا لمتعدد الوجوه وليس وجهًا.^[54] الاستنجام والويجهة عمليتان عكسيتان: ثنويات بعض المُستنجَمات هي ويجهة الثنوي إلى متعدد الوجوه الأصلي.

عائلات أخرى من متعددات الوجوه

متعددات الوجوه المالئة للفضاء

صور لأجزاء من الشِّهَاد المختلفة، المتكونة من متعددات الوجوه المالئة للفراغ. من أعلى اليمين إلى أسفل اليسار: الشهد المكعبي^{[الإنجليزية]}، شهد اثني عشريات الوجوه المعينية^{[الإنجليزية]}، وشهد ثمانيات الوجوه المبتورة^{[الإنجليزية]}، وتشكيلة رؤوس شهد رباعيات الوجوه وثمانياتها^{[الإنجليزية]}.

المقالة الرئيسة: شهد (هندسة)

يَرزُمُ متعدد الوجوه المالئ للفضاء بنسخ من نفسه لملء للفضاء. وغالبًا ما يُطلق على مثل هذا الرَّزْم المتقارب أو ملء الفضاء اسم "رَصْف الفضاء" أو "الشَّهْد". يجب أن يكون لمتعدد الوجوه المالئ للفضاء لامتغير دين يساوي صفرًا. تتضمن بعض الشِّهَاد أكثر من نوع واحد من متعددات الوجوه.

متعددات الوجوه الانثنائية

المقالة الرئيسة: متعدد وجوه انثنائي^{[الإنجليزية]}

من الممكن لبعض متعددات الوجوه تغيير هيئتها الكلية، مع الحفاظ على هيئات وجوهها كما هي، وذلك عن طريق تغيير زوايا حروفها. يُسمَّى متعدد الوجوه الذي يمكنه فعل ذلك بمتعدد الوجوه الانثنائي. وفقًا لمبرهنة كوتشي للجَسَاءَة^{[الإنجليزية]}، يجب أن يكون متعدد الوجوه الانثنائي غير محدب. يجب أن يظل حجم متعدد الوجوه الانثنائي ثابتًا أثناء انثناءه، وتُعرف هذه النتيجة بمبرهنة الكِير.^[56]

متعددات الوجوه المثالية

المقالة الرئيسة: متعدد وجوه مثالي^{[الإنجليزية]}

يمكن تعريف متعددات الوجوه المحدَّبة في الفضاء الزائدي^{[الإنجليزية]} ثلاثي الأبعاد بالطريقة نفسها التي تُعرَّف بها في الفضاء الإقليدي، باعتبارها أغلفة محدَّبة لمجموعات منتهية من النقاط. لكن، في الفضاء الزائدي، من الممكن أيضًا التفكير في النقاط المثالية^{[الإنجليزية]} والنقاط داخل الفضاء. متعدد الوجوه المثالي^{[الإنجليزية]} هو الغلاف المحدب لمجموعة منتهية من النقاط المثالية.^[57] وجوهه مضلعاتٍ مثالية، لكن حروفه محددة بخطوط زائدية كاملة بدلًا من قطع مستقيمة، ورؤوسه (النقاط المثالية التي يمثل غلافها المحدب) لا تقع داخل الفضاء الزائدي.

متعددات الوجوه الشَّبِيكيّة

يُطلَق على متعدِّدات الوجوه المحدَّبة التي تحتوي جميع رؤوسها على إحداثيات صحيحة متعدِّدات الوجوه الشبيكية^{[الإنجليزية]} أو متعدِّدات الوجوه الصحيحة. يحسب كثير حدود إيرهارت^{[الإنجليزية]} لمتعدد الوجوه الشبيكي عدد النقاط ذات الإحداثيات الصحيحة التي تقع داخل نسخة مضبوطة المقاس من متعدد الوجوه، باعتباره دالةً لعامل المقاس. تقع دراسة كثيرات الحدود هذه عند تقاطع التوافيقيات والجبر التبديلي.^[58] مثال على ذلك رباعي وجوه ريف^{[الإنجليزية]}.^[59]

يوجد تكافؤ بعيد المدى بين متعددات الوجوه الشبيكية وبعض المُنوَّعات الجبرية التي تسمى المُنَوَّعَات الطارية^{[الإنجليزية]}.^[60] وقد استخدم ستانلي هذا لإثبات معادلات دين وسومرفيل^{[الإنجليزية]} لمتعددات الأكناف المبسطة^{[الإنجليزية]}.^[61]

مُركَّب متعددات الوجوه

مُركَّب خمسة رباعيات الوجوه^{[الإنجليزية]}، النموذج 25 لِوينِنْغَر^{[الإنجليزية]}

يتكون مُركَّب متعددات الوجوه^{[الإنجليزية]} من اثنين أو أكثر من متعددات الوجوه التي تشترك في مركز مشترك. وغالبًا ما تشترك المُركَّبات المتناظرة في نفس الرؤوس التي تشترك فيها متعددات الوجوه الأخرى المعروفة، وقد تتشكل أيضًا في كثير من الأحيان عن طريق الاستنجام. وبعضها مدرج في قائمة نماذج ويننغر لمتعددات الوجوه^{[الإنجليزية]}.

متعددات الوجوه النُّطُقيّة

متعدد وجوه نطقي هو متعدد وجوه محدب يكون كل وجه فيه مضلعًا متناظرًا تحت الدوران حتى 180 درجة. يمكن أيضًا وصف متعددات الوجوه النطقية على أنها مجاميع منكوفسكي^{[الإنجليزية]} للقطع المستقيمة، وتشمل العديد من متعددات الوجوه المهمة المالئة للفضاء.^[62]

متعددات الوجوه المتعامدة

المقالة الرئيسة: متعدد وجوه متعامد^{[الإنجليزية]}

بعض متعددات الوجوه المتعامدة^{[الإنجليزية]} المصنوعة من قطع مكعبات سوما، وهي نفسها متعددات المكعبات

يُقال إن متعددات الوجوه متعامدة^{[الإنجليزية]} لأن جميع حروفها موازية لمحاور نظام الإحداثيات الديكارتية. هذا يعني أن جميع الوجوه تلتقي عند زوايا قائمة، لكن هذا الشرط أضعف: فعشروني وجوه يسن^{[الإنجليزية]} له وجوه تلتقي عند زوايا قائمة، لكن ليس له حروف مُوَازية للمحاور. وبصرف النظر عن متوازيات المستطيلات، فإن متعددات الوجوه المتعامدة غير محدَّبة. إنها المثائل الثلاثية الأبعاد للمضلعات المتعامدة الثنائية الأبعاد، والمعروفة أيضًا باسم المضلعات القائمة الزوايا^{[الإنجليزية]}. تُستخدم متعددات الوجوه المتعامدة في الهندسة الحوسبية، حيث مكنت بنيتها المقيدة من إحراز تقدم في المسائل التي لم تُحل في حالة متعددات الوجوه الكيفية، على سبيل المثال، بَسْط سطح متعدد وجوه إلى شبكة مضلعية.^[63] تعد متعددات المكعبات حالة خاصة من متعددات الوجوه المتعامدة التي يمكن تفكيكها إلى مكعبات متطابقة، وهي مثائل ثلاثية الأبعاد للدومينوات المتعددة^{[الإنجليزية]} المستوية.^[64]

التعميمات

لقد أصبح اسم "متعدد الوجوه" يُستخدم لمجموعة متنوعة من الكائنات التي لها خصائص بنيوية مشابهة لمتعددات السطوح التقليدية.

لامنتهيات الوجوه

لامنتهي الوجوه المسمى مِيكِيب (Mucube)

يحتوي سطح متعدد الوجوه الكلاسيكي على عدد محدود من الوجوه، مرتبطة في أزواج على طول الحروف. تُشكِّل لامنتهيات الوجوه^{[الإنجليزية]} صنفًا ذا صلة من الكائنات ذات الوجوه غير المنتهية. تتضمَّن أمثلة على لامنتهيات الوجوه ما يلي:

• تبليطات أو رُصُوف للمستوي،
• والبنى الشبيهة بالإسفنج التي تسمى لامنتهيات الوجوه المتخالفة^{[الإنجليزية]}.

متعددات الوجوه العُقَدِيَّة

المقالة الرئيسة: متعدد أكناف عقدي^{[الإنجليزية]}

توجد كائنات تُسمَّى متعددات الوجوه العقدية، والتي يكون الفضاء الأساسي لها هو فضاء هلبرت العُقدي وليس الفضاء الإقليدي الحقيقي. لا توجد تعريفات دقيقة إلا لمتعددات الوجوه العقدية المنتظمة، التي تكون زمر التناظر الخاصة بها زمر انعكاس عُقدية^{[الإنجليزية]}. ترتبط متعددات الوجوه العقدية رياضيًّا بالتشكيلات^{[الإنجليزية]} أكثر من ارتباطها بمتعددات الوجوه الحقيقية.^[65]

متعددات الوجوه المنحنية

تسمح بعض مجالات الدراسة بأن يكون لمتعدد الوجوه وجوه وحروف منحنية. يمكن أن تسمح الوجوه الثنائية الجوانب بوجود وجوه منحنية ذات مساحة موجبة.

• عندما يُقسَّم سطح الكرة على عدد منتهٍ من الأقواس العظمى (أيْ بمُستوِيات تمر عبر مركز الكرة)، تُسمَّى النتيجة متعدد الوجوه الكروي. يمكن إسقاط العديد من متعددات الأكناف المحدَّبة التي لها درجة ما من التناظر (على سبيل المثال، جميع المجسَّمات الأفلاطونية) على سطح كرة متحدة المركز لإنتاج متعدد الوجوه الكروي. ومع ذلك، فإن العملية العكسية ليست ممكنة دائمًا؛ فبعض متعددات الوجوه الكروية (مثل كَثُورات الوجوه^{[الإنجليزية]}) ليس لها مماثل مسطح الوجوه.^[66]
• إذا سُمح للوجوه أن تكون مقعرة ومحدبة أيضًا، فيمكن جعل الوجوه المتجاورة تلتقي معًا دون وجود فجوة. يمكن لبعض متعددات الوجوه المنحنية هذه أن تَرزُم معًا لملء الفضاء. يوجد نوعان مهمان هما الفقاعات في الزَّبَد والرغاوي مثل فقاعات وير وفيلان^{[الإنجليزية]}،^[67] والأشكال المستخدمة في العمارة.^[68]

متعددات وجوه ذات أبعاد أعلى

المقالة الرئيسة: متعدد وجوه نوني الأبعاد^{[الإنجليزية]}

منذ النصف الأخير من القرن العشرين، وُجد أن العديد من الإنشاءات الرياضياتية لها خصائص موجودة أيضًا في متعددات الوجوه التقليدية. وبدلًا من حصر مصطلح "متعدد الوجوه" في وصف متعدد الأكناف ثلاثي الأبعاد، اعتُمد لوصف أنواع مختلفة من البينات ذات الصلة ولكن متميزة.

عُرِّف متعدد الوجوه على أنه مجموعة من النقاط في فضاء حقيقي تآلفي (أو إقليدي) من أي بُعد n له جوانب مسطحة. ويمكن تعريفه بدلًا من ذلك على أنه تقاطع عدد منتهٍ من أنصاف الأفضية^{[الإنجليزية]}. وخلافًا لمتعدد السطوح الاصطلاحي، قد يكون متعدد الوجوه محدودًا أو غير محدود. وبهذا المعنى، فإن متعدد الأكناف هو متعدد وجوه محدود.^[14][15]

من الناحية التحليلية، يُعبَّر عن مثل متعدد الوجوه المحدَّب هذا تحليليًّا باعتباره مجموعة حلول لمنظومة من المتراجحات الخطية. يوفِّر تعريف متعدِّدات الوجوه بهذه الطريقة منظورًا هندسيًّا للمسائل في البرمجة الخطية.^[69]

نبذة تاريخية

قبل الإغريق

المسألة رقم 14 من بردية موسكو الرياضية، حول حساب حجم الجذع

ظهرت متعددات الوجوه في أوائل الأشكال المعمارية مثل المكعبات ومتوازيات المستطيلات، ويعود تاريخ أقدم الأهرام المصرية رباعية الأضلاع إلى القرن السابع والعشرين قبل الميلاد.^[70] تتضمن بردية موسكو الرياضية التي تعود إلى قرابة 1800-1650 قبل الميلاد أحد أولى دراسات مكتوبة عن متعددات الوجوه وأحجامها (وتحديدًا حجم الجذع).^[71] كما تضمنت رياضيات الإمبراطورية البابلية القديمة، التي تعود إلى نفس الفترة الزمنية تقريبًا التي ظهرت فيها بردية موسكو، حسابات أحجام متوازيات المستطيلات (وأسطوانات غير متعددة الوجوه)، وحسابات ارتفاع هذا الشكل اللازم للوصول إلى حجم معين.^[72]

سبق الإتروريون الإغريق في إدراكهم لبعض متعددات الوجوه المنتظمة على الأقل، كما يتضح من اكتشاف اثنعشريات الوجوه الإترورية المصنوعة من الحجر الصابوني في مونتي لوفا^{[الإنجليزية]}. وقد وُسِمَت أوجهه بتصاميم مختلفة، مما يوحي لبعض العلماء أنه ربما استُخدِم زهرًا للنرد.^{[وب-إنج 3]}

الإغريق

العناصر الخمسة مرسومة في مجسمات أفلاطونية كما رسمها كبلر في كتابه "تناغم العالم"

اكتشف علماء الرياضيات الإغريق ودرسوا متعددات الوجوه المحدبة المنتظمة، والتي عُرفت باسم المجسمات الأفلاطونية. ويرد أول وصف مكتوب لها في حوار لأفلاطون يحمل اسم طيماوس (قرابة 360 قبل الميلاد)، والذي يربط أربعة منها بالعناصر الأربعة والخامس بالشكل العام للكون. كُتبت معالجة رياضياتية أكثر لمتعددات الوجوه الخمسة هذه بعد فترة وجيزة في كتاب الأصول لإقليدس. كتب أحد الشارحين الأوائل عن إقليدس (ربما جيمينوس) أن نسبة هذه الأشكال إلى أفلاطون غير صحيحة: فقد عَرَف فيثاغورس رباعي الوجوه والمكعب وعشروني الوجوه، واكتشف ثياتيتوس (نحو 417 قبل الميلاد) الشكلين الآخرين، وهما ثماني الوجوه عشروني الوجوه.^[73] وسَّع أرخميدس دراسته في وقت لاحق لتشمل متعددات الوجوه المحتتنة المحدبة التي تحمل اسمه الآن، لكن عمله الأصيل ضاع، ولم يبقلى منه إلا مجسماته التي ذكرها ببس الرومي.^[74]

الصين القديمة

زهر نرد ذو أربعة عشر وجهًا يعود إلى حقبة الممالك المتحاربة

يعود تاريخ كل من زهر النرد المكعب وزهر النرد ذي الأربعة عشر وجهًا على شكل ثماني وجوه مبتور^{[الإنجليزية]} في الصين إلى حقبة الممالك المتحاربة.^[75]

وصف ليو هوي بحلول عام 236 الميلادية تقطيع المكعب إلى رباعي الوجوه المميز له (مُبسَّط قائم^{[الإنجليزية]}) والمجسمات ذات الصلة، مستخدمًا تجميعات هذه المجسمات باعتبارها أساسًا لحساب أحجام التربة التي يجب نقلها أثناء الحفريات الهندسية التطبيقية.^[76]

العصر الذهبي للإسلام

طالع أيضًا: الرياضيات في عصر الحضارة الإسلامية

ساهم علماء الحضارة الإسلامية في الحفاظ على المعرفة الإغريقية المرتبطة بمتعددات الوجوه ونقلها إلى الأجيال التالية بترجمتها إلى العربية.^[77] ثم أضافوا عليها من اكتشفاتهم، فأدرج ثابت بن قرة مثلًا في القرن التاسع الميلادي حساب الأحجام في دراساته،^{[عر 7]} وكتب عملاً عن ذي الوجوه المكعبي الثماني. بعد ذلك وصف أبو الوفاء البوزجاني في القرن العاشر الميلادي متعددات الوجوه الكروية شبه المنتظمة ومتعددات الوجوه المنتظمة المحدبة.^[78]

عصر النهضة

صورة ثنائية^{[الإنجليزية]}، منسوبة إلى ياكوبو دي بارباري، تُصوِّر لوكا بتشولي وتلميذ يدرس ذو الوجوه المكعبي الثماني المعيني من الزجاج نصف مملوء بالماء.^[79]

رسم ليوناردو دافنشي لمتعدد وجوه هيكلي (وتحديدًا ذو الوجوه المكعبي الثماني المعيني) لتصوير كتاب لِلوكا بتشولي

كما هو الحال مع مجالات أخرى من الفكر اليوناني التي حافظ عليها العلماء المسلمون وعززوها، انتعش الاهتمام الغربي بمتعددات الوجوه خلال عصر النهضة الإيطالية. حيث أنشأ الفنانون متعددات وجوه هيكلية وصوروها من الحياة باعتبارها جزءًا من تحقيقاتهم في المنظور.^[80] أصبحت متعددات الوجوه الطارانية^{[الإنجليزية]} المصنوعة من الخشب والمستخدمة لدعم العَمَرَات، تمرينًا شائعًا في الرسم المنظوري، وصُوِّرت في اللوحات الخشبية المُطَعَّمَة في تلك الفترة باعتبارها رمزًا للهندسة.^[81] كتب بييرو ديلا فرانشيسكا عن إنشاء مناظر منظورية لمتعددات الوجوه وأعاد اكتشاف العديد من المجسمات الأرخميدية. رسم ليوناردو دا فنشي نماذج هيكلية للعديد من متعددات الوجوه لتدوينها في كتاب للوكا بتشولي،^[82] مع نص مُنتَحَل إلى حد كبير من ديلا فرانشيسكا.^[83] ظهرت شبكات متعددات الوجوه في أعمال ألبرشت دورر.^[84]

تبحث العديد من الأعمال من تلك الفترة في متعددات الوجوه النجمية وغيرها بتفاصيل الأشكال الأفلاطونية الأساسية. توجد تَرْسِيَة^{[الإنجليزية]} رخامية في أرضية كنيسة القديس مرقس في البندقية، صممها باولو أوتشيلو، وهي تُصوِّر اثنعشري وجوه مستنجم.^[85] ومع انتشار عصر النهضة إلى خارج إيطاليا، صوّر فنانون لاحقون مثل فِنْتسل يَمْنِتْسَر^{[الإنجليزية]} ودُورَر وغيرهما أيضًا متعددات وجوه متزايدة التعقيد، وكثير منها جديد، في تنميشات إبداعية.^[86] استخدم يوهانس كبلر (1571-1630) المضلعات النجمية، وهي عادةً نجوم مُخَمَّسِيَّة، لإنشاء متعددات وجوه نجمية. ربما اكتُشفت بعض هذه الأشكال قبل زمن كبلر، لكنه كان أول من أدرك أنه يمكن اعتبارها ”منتظمة“ إذا أزالنا القيد الذي ينص على أن متعددات الوجوه المنتظمة يجب أن تكون مُحدَّبة.^[74]

ذُكِرَت صيغة أويلر لمتعددات الوجوه في الفترة نفسها، وهي معادلة خطية تربط بين عدد رؤوس متعدد الوجوه وعدد حروفه ووجوهه، للمجسمات الأفلاطونية في عام 1537م في مخطوطة غير منشورة لفرانشيسكو موروليكو.^[87]

بين القرنين 17 و19

ألَّف رينيه ديكارت، قرابة عام 1630، كتابه "حول عناصر المجسمات^{[الإنجليزية]}" الذي يدرس فيه متعددات الوجوه المحدبة باعتباره مفهومًا عامًا، لا يقتصر على المجسمات الأفلاطونية وتفاصيلها. وقد فُقد هذا العمل ولم يعاد اكتشافه حتى القرن التاسع عشر. كانت إحدى إسهاماته مبرهنة ديكارت عن العيب الزاوي الكلي^{[الإنجليزية]}، والتي ترتبط ارتباطًا وثيقًا بصيغة أويلر لمتعددات الوجوه.^[88] قدم ليونهارت أويلر، الذي سُميت الصيغة باسمه، هذه الصيغة في عام 1758 لمتعددات الوجوه عمومًا، وإن كان ذلك مع برهان غير صحيح.^[89] أصبح عمل أويلر، مع الحل الذي سبق وقدمه لأحجية جسور كونيغسبرغ السبعة، أساس المجال الجديد للطبولوجيا.^[90] طوّر هنري بوانكاريه وإنريكو بيتي^{[الإنجليزية]} وبرنهارت ريمان وآخرون في أواخر القرن التاسع عشر المفاهيم الأساسية لهذا المجال، بما في ذلك تعميمات صيغة متعددات الوجوه.^[91]

وسَّع لويس بوانسو نطاق عمل كبلر في أوائل القرن التاسع عشر، واكتشف متعددَيْ الوجوه النجميين المنتظمين المتبقيين. أثبت أغسطين لويس كوشي بعد فترة وجيزة اكتمال قائمة بوانسو، مع مراعاة افتراض غير مذكور بأن تسلسل رؤوس وحروف كل جانب مضلعي لا يمكن أن يقبل التكرار (وهو افتراض أُخذ بعين الاعتبار ولكن رُفِضَ في الأعمال الأولى لألبرشت لودفيغ فريدريش مايستر^{[الألمانية]}).^[92] أصبحت تعرف باسم متعددات وجوه كبلر وبوانسو، وأطلق آرثر كيلي عليها أسماءها المعتادة.^{[وب-إنج 4]} وفي الوقت نفسه، قاد اكتشاف الأبعاد الأعلى في أوائل القرن التاسع عشر لودفيغ شليفلي^{[الإنجليزية]} بحلول عام 1853 إلى فكرة متعددات الأكناف عالية الأبعاد.^[93] بالإضافة إلى ذلك، في أواخر القرن التاسع عشر، أكمل عالم البلورات الروسي يفغراف فيودوروف تصنيف متوازيات الوجوه، وهي متعددات الوجوه المحدبة التي تبلّط الفضاء عن طريق الانسحابات.^{[وب-إنج 5]}

بين القرنين 20 و21

طرح الرياضياتي الألماني ديفيد هلبرت مجموعة مسائل في المؤتمر الدولي للرياضيات في باريس عام 1900م، سميت مسائل هلبرت، وقال أنها ستحدد شكل الرياضيات في القرن المقبل، لأن لها صلات وجذور بفروع متعددة من الرياضيات. وكانت إحدى هذه المسائل، وهي مسألة هلبرت الثالثة^{[الإنجليزية]}، تتعلق بمتعددات الوجوه وتقطيعها. وسرعان ما حُلَّت على يد تلميذ هلبرت ماكس دين، عندما قدم لامتغير دين لمتعددات الوجوه.^[94] وقد ميزت مبرهنة شتاينتس^{[الإنجليزية]} التي نشرها إرنست شتاينتس^{[الإنجليزية]} عام 1992، بيانات متعددات الوجوه المحدبة، حيث أدخلت الأفكار الحديثة من نظرية البيان والتوافيقيات في دراسة متعددات الوجوه^{[الإنجليزية]}.^[95]

يمكن إنشاء متعددات الوجوه كبلر وبوانسو من المجسمات الأفلاطونية عن طريق عملية تُسمَّى الاستنجام. معظم الاستنجامات ليست منتظمة. أعطى هارولد كوكستر وآخرون دفعة كبيرة لدراسة استنجامات المجسمات الأفلاطونية في عام 1938، مع المقالة البحثية الشهيرة الآن "عشرونيات الوجوه التسعة والخمسون^{[الإنجليزية]}".^[96] أشار تحليل كوكستر إلى ولادة جديدة للاهتمام بالهندسة. مضى كوكستر نفسه في تعداد متعددات الوجوه المحتتنة النجمية أول مرة، ومعالجة تبليطات المستوي على أنها متعددات وجوه، واكتشاف متعددات الوجوه المتخالفة المنتظمة^{[الإنجليزية]}، وتطوير نظرية متعددات الوجوه العُقدية^{[الإنجليزية]} التي اكتشفها شيبارد أول مرة في عام 1952، بالإضافة إلى تقديم مساهمات أساسية في العديد من مجالات الهندسة الأخرى.^[97]

أشار كل من برانكو غرونباوم^{[الإنجليزية]} وإمره لاكاتوش في الجزء الثاني من القرن العشرين إلى ميل علماء الرياضيات إلى تعريف ”متعدد الوجوه“ بطرق مختلفة وأحيانًا غير متوافقة لتناسب احتياجات اللحظة.^[2] في سلسلة من المقالات البحثية، وسّع غرونباوم التعريف المقبول لمتعدد الوجوه، واكتشف العديد من متعددات الوجوه المنتظمة الجديدة. اندمجت هذه الأفكار الأخيرة في نهاية القرن العشرين مع أعمال أخرى حول مُركَّبَات الوقوع لتكوين الفكرة الحديثة لمتعدد الوجوه المجرد (باعتباره متعدد الأكناف المجرد ثلاثي الأبعاد)، ولا سيما تلك التي قدمها ماكمولن وشولته.^[98]

الشَّعُوعِيَّة «المُستديرة الزاوِيَّة عشرونية الوجوه» (الاسم العلمي: Circogonia icosahedra)

خريطة دَيْمَكْسِيُون^{[الإنجليزية]}، التي أُنشئت بشبكة عشريني الوجوه المنتظم

اكتُشفت متعددات الوجوه في العديد من مجالات العلوم. فقد ظهرت المجسمات الأفلاطونية في الكائنات الحية، كما هو الحال في كرة بِغْلَو البُّرُورُوِيَّة^{[الإنجليزية]} التي تمتلك بنية عشريني الوجوه المنتظم.^[99] وصف إرنست هيكل عددًا من أنواع الشَّعُوعِيَّات، التي تتشكل بعض أصدافها على شكل متعددات وجوه منتظمة مختلفة.^{[ألم 2]} وتُشَكِّل الأصداف البروتينية الخارجية للعديد من الفيروسات متعددات الوجوه المنتظمة. على سبيل المثال، فيروس العوز المناعي البشري (HIV) محاط بعشروني وجوه منتظم، وكذلك رأس الفيروس العضلي النمطي.^[100] وقد ظهر عشروني الوجوه المنتظم أيضًا في تطبيقات الخرائطية عندما استخدم ر. بوكمينستر فولر شبكته في مشروعه المعروف باسم خريطة ديمكسيون^{[الإنجليزية]}، وأدرك بإحباط أن حجم غرينلاند أصغر من حجم أمريكا الجنوبية.^[101]

يتكرر ظهور متعددات الوجوه في الهندسة الحوسبية الحديثة والرسوميات الحاسوبية والتصميم الهندسي^{[الإنجليزية]} خاصةً إعادة إنشاء السطوح المتعددة الوجوه أو شبكات السطح المضلعاتية من نقاط المعطيات المتبعثرة،^[102] والخطوط المتقاصرة على السطوح المتعددة الوجوه،^[103] وقابلية الرؤية^{[الإنجليزية]} والإضاءة في مشاهد متعددات الوجوه،^[104] ومتعددات المكعبات ومتعددات الوجوه الأخرى غير المحدبة ذات الجوانب الموازية للمحاور،^[105] والأشكال الخوارزمية لمبرهنة شتاينتس،^[106] والمسألة التي لم تُحل بعد المتمثلة في وجود شبكات لمتعددات الوجوه المحدبة.^[107]

معرض صور

• 
  متعدد وجوه طاراني (${\displaystyle T^{2}}$) يتكون من 48 مثلثًا متساوي الأضلاع
• 
  يمتلك عشروني الوجوه المبتور (على اليسار) 30 وجهًا، 20 منها مخمسة و12 منها مسدسة،^[ه] إن الحالة الكروية له هي كرة القدم المعتادة
• 
  بلورتَا بيريت مكعبة
• 
  بلورة بجادي ذات شكل اثني عشري الوجوه المعينية
• 
  ليوسيت مع أوجيت، الأول على شكل مجسم ذي 24 وجهًا حدئيًا
• 
  مثال عن قبة متقاصرات^[و] مسماة الأرض سفينة الفضاء^{[الإنجليزية]} في عالم والت ديزني بفلوريدا
• 
  ثماني الوجوه المستنجم^{[الإنجليزية]}، هي نسخة مُوَيْجَهَة من المكعب
• 
  نموذج هيكل^{[الإنجليزية]} مكعب مبتور في الفضاء

انظر أيضًا

• متعدد وجوه شازيل^{[الإنجليزية]}
• تمديد متعدد وجوه^{[الإنجليزية]}
• متعدد وجوه غولدبرغ^{[الإنجليزية]}
• قائمة الكتب عن متعددات الوجوه^{[الإنجليزية]}
• مجسم مقارب لمجسم جونسون^{[الإنجليزية]}
• نموذج متعدد وجوه^{[الإنجليزية]}
• عدد شكلي
• نظرية الأزواج الإلكترونية الهيكلية لمتعدد الوجوه^{[الإنجليزية]}
• فضاء متعدد وجوه^{[الإنجليزية]}
• رمز متعدد وجوه^{[الإنجليزية]}
• تضريس متعدد الوجوه^{[الإنجليزية]}
• نموذج متعدد أكناف^{[الإنجليزية]}
• ستيلا (برمجية)^{[الإنجليزية]}

الملاحظات

1. النص الأصيل: (بالإنجليزية: The Original Sin in the theory of polyhedra goes back to Euclid, and through Kepler, Poinsot, Cauchy and many others... at each stage... the writers failed to define what are the polyhedra)
2. يمكن تمثيل الخاصية الطبولوجية لمتعدد الوجوه المتساوية بتشكيل الوجوه. جميع المجسمات الأفلاطونية الخمسة ومجسمات كاتالان الثلاثة عشر متساوية الوجوه، وكذلك العائلات غير المنتهية من حدئيات الوجوه وثنائيات الأهرام. تسمح بعض تعريفات متساويات الوجوه بتنوعات هندسية تشمل الأشكال المقعرة وذاتية التقاطع.
3. هذا هو أحد التعريفات العديدة للمصطلح، اعتمادًا على المؤلف. تتداخل بعض التعريفات مع صنف متعددات الوجوه شبه المنتظمة.
4. كانت المجسمات الأرخميدية تحتوي في السابق على مجسم رابع عشر يُعرف باسم ذو الوجوه المكعبي الثماني المعيني الزائف^{[الإنجليزية]}، وهو إنشاء خاطئ لذي الوجوه المكعبي الثماني المعيني. ومع ذلك، استُبعد لعدم امتلاكه خاصية الانتقال بين الرؤوس^{[الإنجليزية]}، مما أدى إلى تصنيفه بدلاً من ذلك على أنه مُجسَّم جُنسون.^[44]
5. لا يُمكن إنشاء مُتعدد وجوه بحيث تكون جميع رؤوسه تشترك فيها ثلاثة أحرف، وتكون جميع وجوهه مسدسة.
6. قبة المتقاصرات هي من أشكال متعددات الوجوه الكروية، وهي بنية قشرية رقيقة كروية جزئيًا أو كليًا مبنية على أساس شبكة من الدوائر العظمى (الخطوط المتقاصرة) على سطح الكرة.

مسرد

مرتب وفق الألفبائية الإنجليزية
#
متعدد أكناف ثلاثي الأبعاد	3-polytope
متعدد أكناف رباعي الأبعاد	4-polytope
A
متعدد وجوه مجرد	Abstract polyhedron
متعدد وجوه غير ذاتي التقاطع	Acoptic polyhedron
مبرهنة ألكسندروف للوحدانية	Alexandrov's uniqueness theorem
منوعة جبرية	Algebraic variety
خوارزمية	Algorithm
عيب زاوي	Angular defect
حلقة	Annulus
موشور تخالفي	Antiprism
تناظر ضد موشوري	Antiprismatic symmetry
لامنتهيات الوجوه	Apeirohedron
قمة (لشكل هندسي)	Apex
قوس	Arc
مجسم أرخميدي	Archimedean solid
محور	Axis
B
قاعدة (لشكل هندسي)	Base
مبرهنة الكير	Bellows theorem
ثنائي هرم	Bipyramid
مبرهنة بوياي وغيرفين	Bolyai–Gerwien theorem
حدود	Boundary
متعدد وجوه محدود	Bounded polyhedron
كرة بِغْلَو البُّرُورُوِيَّة	Braarudosphaera bigelowii
مبرهنة الفراشة	Butterfly theorem
C
متعدد وجوه قانوني	Canonical polyhedron
مجسم كاتالان	Catalan solid
مبرهنة كوشي للجَسَاءة	Cauchy's rigidity theorem
خلية	Cell
مُجمَّع خلوي	Cell complex
مركز (لشكل هندسي)	Centroid
يدوانية	Chirality
زمرة متعدد وجوه يدوانية	Chiral polyhedral group
كرة محيطة	Circumsphere, Circumscribed sphere
تصنيف المتنوعات	Classification of manifolds
توافيقي	Combinatorial
توافيقيات	Combinatorics
جبر تبديلي	Commutative algebra
متعدد وجوه عُقدي	Complex polyhedron
زمرة انعكاس عُقدية	Complex reflection group
مُركَّب خمس رباعيات الوجوه	Compound of five tetrahedra
متعدد وجوه مؤلف	Composite polyhedron
هندسة حوسبية	Computational geometry
رسوميات الحاسوب	Computer graphics
تشكيلة	Configuration
مُركِّبة مترابطة	Connected component
غلاف محدب	Convex hull
مضلع محدب	Convex polygon
متعدد وجوه محدب	Convex polyhedron
وضع محدب	Convex position
مجموعة محدبة	Convex set
قبعة متصالبة	Cross-cap
متعدد وجوه تشاسار	Császár polyhedron
مكعب	Cube
شهد مكعبي	Cubic honeycomb
ذو الوجوه المكعبي الثماني	Cuboctahedron
قبة	Cupola
متعدد وجوه منحنٍ	Curved polyhedra
زمرة دورية	Cyclic group
أسطوانة	Cylinder
D
مُنْحَلّ	Degenerate
انحلال	Degeneracy
لامتغير دين	Dehn invariant
معادلات دين وسومرفيل	Dehn–Sommerville equations
دلتاوي وجوه	Deltahedron
ذو 24 وجهًا حدئيًا	Deltoidal icositetrahedron
مبرهنة ديكارت عن العيب الزاوي الكلي	Descartes' theorem on total angular defect
قُطْر	Diagonal
ثنائي الجوانب	Digon
زاوية ثنائية الوجه	Dihedral angle
بُعد	Dimension
تقطيع (شكل هندسي)	Dissection
مبرهنة التباعد	Divergence theorem
اثنا عشري وجوه	Dodecahedron
جداء سُلَّمي	Dot product
ثِنْوِيّ	Dual
متعدد وجوه ثِنْوِيّ	Dual polyhedron
ترتيب جزئي	Dual order
ثِنْوِيَّة	Duality
E
حرف، حافة	Edge
انتقالي الحروف	Edge-transitive
متعدد وجوه ابتدائي	Elementary polyhedron
طَمْر	Embedding
مجموعة خالية	Empty set
هرم مربع متساوي الحروف	Equilateral square pyramid
كثير حدود إرهارت	Ehrhart polynomial
فضاء إقليدي	Euclidean space
مميزة أويلر	Euler characteristic
صيغة أويلر لمتعددات الوجوه	Euler's polyhedral formula
F
وجه	Face
انتقالي الوجوه	Face-transitive
كَنَف (تعميم وجه على أي بعد) وُجَيْه (مضلع تكون زواياه رؤوسًا لمتعدد وجوه وليس وجهًا)	Facet
تشكيل بالوجيهات	Faceting
شكل	Figure
متعدد وجوه انثنائي	Flexible polyhedron
جذع	Frustum
زمرة متعدد وجوه كاملة	Full polyhedral group
G
جنس	Genus
خط متقاصر	Geodesic
تصميم هندسي	Geometric design
بيان	Graph
نظرية البيان	Graph theory
قوس أعظم	Great arc
مُوَازي وجوه مكعبي مكعبي ثماني عظيم	Great cubicuboctahedron
زمرة	Group
H
نصف فضاء	Half-space
تطبيق هيوود	Heawood map
هرم مسدس	Hexagonal pyramid
مسائل هلبرت	Hilbert's problems
مسألة هلبرت الثالثة	Hilbert's third problem
مسألة هلبرت الثامنة عشر	Hilbert's eighteenth problem
فضاء هلبرت	Hilbert space
شَهْد	Honeycomb
كَثور الوجوه	Hosohedra
فضاء زائدي	Hyperbolic space
I
عشروني وجوه	Icosahedron
تناظر عشروني الوجوه	Icosahedral symmetry
ذو الوجوه الاثنا عشري العشروني	Icosidodecahedron
نقطة مثالية	Ideal point
متعدد وجوه مثالي	Ideal polyhedron
هندسة الوقوع	Incidence geometry
كرة محاطة	Insphere, Inscribed sphere
عدد صحيح	Integer
متعدد وجوه صحيح	Integral polyhedra
متساوي الرؤوس	Isogonal
متساوي الوجوه (صفة)	Isohedral
متساوي وجوه	Isohedron
متساوي الحروف	Isotoxal
J
عشروني وجوه ييسن	Jessen's icosahedron
مجسم جونسون	Johnson solid
K
متعدد وجوه كبلر وبوانسو	Kepler–Poinsot polyhedron
قارورة كلاين	Klein bottle
L
شَبِيكة	Lattice
متعدد وجوه شَبِيكي	Lattice polyhedron
معادلة خطية	Linear equation
قطعة مستقيمة	Line segment
M
مُتنوِّعة	Manifold
تطبيق	Map, mapping
فضاء متري	Metric space
كرة وسيطة	Midsphere
مجموع منكوفسكي	Minkowski sum
شريط موبيوس	Möbius strip
بردية موسكو الرياضية	Moscow Mathematical Papyrus
N
متعدد وجوه نوني الأبعاد	n-dimensional polyhedron
متعدد وجوه نبيل	Noble polyhedron
متعدد وجوه غير محدب	Non-convex polyhedron
O
ثماني وجوه	Octahedron
تناظر ثماني الوجوه	Octahedral symmetry
ترتيب معاكس	Opposite order
قابل للتوجيه	Orientable
قابلية التوجيه	Orientability
متعدد وجوه متعامد	Orthogonal polyhedron
مُبسَّط قائم	Orthoscheme
P
متوازي وجوه	Parallelepiped
متوازي متعدد الوجوه	Parallelohedron
مجموعة مرتبة جزئيًا	Partially ordered set
ترتيب جزئي	Partial order
عمودي	Perpendicular
مخمس نجمي	Pentagram
منظور	Perspective
بيان مستوٍ	Planar graph
مستوٍ	Plane
مجسم أفلاطوني	Platonic solid
زمرة نقطية	Point group
تحويل معاكس قطبي	Polar reciprocation
متعدد مكعبات	Polycube
مضلع	Polygon
شبكة مضلعية	Polygonal net
سطح متعدد الوجوه	Polyhedral surface
مُركَّب متعددات وجوه	Polyhedral compound
متعدد وجوه	Polyhedron
زمرة متعدد وجوه	Polyhedral group
دومينو متعدد	Polyomino
متعدد أكناف	Polytope
موشور	Prism
تناظر موشوري	Prismatic symmetry
موشور متوازي الوجهين	Prismatoid
ذو الوجوه المكعبي الثماني المعيني الزائف	Pseudorhombicuboctahedron
هرم	Pyramid
تناظر هرمي	Pyramidal symmetry
بيريتي وجوه	Pyritohedron
تناظر بيريتي	Pyritohedral symmetry
Q
شبه منتظم	Quasiregular
R
الشَّعُوعيّات	Radiolarians
تحقيق	Realization
مستو إسقاطي حقيقي	Real projective plane
متوازي مستطيلات	Rectangular cuboid
مضلع مستقيم	Rectilinear polygon
رباعي وجوه ريف	Reeve tetrahedron
انعكاس	Reflection
تناظر انعكاسي	Reflection symmetry
مضلع منتظم	Regular polygon
متعدد وجوه منتظم	Regular polyhedron
شهد اثني عشريات الوجوه المعينية	Rhombic dodecahedral honeycomb
اثنا عشري وجوه معينية	Rhombic dodecahedron
ذو الوجوه المكعبي الثماني المعيني	Rhombicuboctahedron
ثلاثوني وجوه معينية	Rhombic triacontahedron
زاوية قائمة	Right angle
دوران	Rotation
طارمة	Rotunda
انعكاس دوراني	Rotoreflection
S
مَقَاس	Scale
متعدد وجوه شونهارت	Schönhardt polyhedron
متعدد وجوه ذاتي التقاطع	Self-crossing polyhedron
نصف منتظم	Semiregular
جسور كونيغسبرغ السبعة	Seven Bridges of Königsberg
هيئة، شكل	Shape
مضلع بسيط	Simple polygon
مُبسَّط	Simplex
متعدد أكناف مبسطة	Simplicial polytope
هيكل	Skeleton
متعدد وجوه متخالف	Skew polyhedron
تشريح	Slicing
اثنا عشري وجوه مستنجم صغير	Small stellated dodecahedron
ذو الوجوه المكعبي الثماني الأفطس	Snub cuboctahedron
ذو الوجوه الاثنا عشري العشروني الأفطس	Snub icosidodecahedron
مجسم	Solid
شكل مجسم	Solid figure
متعدد وجوه مجسم	Solid polyhedron
متعدد وجوه مالئ للفضاء	Space-filling polyhedron
متعدد وجوه كروي	Spherical polyhedron
هرم مربع	Square pyramid
متعدد وجوه نجمي	Star polyhedron
مبرهنة شتاينتس	Steinitz's theorem
اثنا عشري وجوه مستنجم	Stellated dodecahedron
استنجام	Stellation
مبرهنة الكير القوي	Strong bellows theorem
بنية	Structure
سطح	Surface
مساحة سطح	Surface area
شبكة سطح	Surface mesh
تناظر	Symmetry
زمرة تناظر	Symmetry group
عملية تناظر	Symmetry operation
مدار تناظر	Symmetry orbit
متعدد وجوه سيلاشي	Szilassi polyhedron
T
مُماس	Tangent
رَصْف	Tessellation
رباعي وجوه	Tetrahedron
تناظر ثلاثي الوجوه	Tetrahedral symmetry
موازي وجوه رباعي نصف سداسي	Tetrahemihexahedron
طيماوس	Timaeus
قرص طبولوجي	Topological disk
كرة طبولوجية	Topological sphere
طبولوجيا	Topology
طاراني	Toroid
طاراني	Toroidal
متعدد وجوه طاراني	Toroidal polyhedron
مُنوَّعة طارية	Toric variety
طارة	Torus
انسحاب	Translation
حدئي وجوه	Trapezohedron
شبه منحرف	Trapezoid
عشروني وجوه مثلوثة	Triakis icosahedron
موشور مثلث	Triangular
تثليث زاوي	Triangulation
موشور مثلث ثلاثي الزيادة	Triaugmented triangular prism
عشروني وجوه مبتور	Truncated icosahedron
رباعي وجوه مبتور	Truncated tetrahedron
ثماني وجوه مبتور	Truncated octahedron
شهد ثمانيات الوجوه المبتورة	Truncated octahedral honeycomb
شهد رباعيات الوجوه وثمانياتها	Tetrahedral-octahedral honeycomb
ثنائي الأبعاد	Two-dimensional
ثلاثي الأبعاد	Three-dimensional
U
متعدد وجوه غير أمين	Unfaithful polyhedron
متعدد وجوه مُحتَتِن	Uniform polyhedron
متعدد وجوه نجمي مُحتَتِن	Uniform star polyhedron
متجه الوحدة	Unit vector
V
مُنوَّعة	Variety
متجه	Vector
رأس	Vertex
تشكيلة رأس	Vertex configuration
انتقالي الرؤوس	Vertex-transitive
شكل الرأس	Vertex figure
حجم	Volume
W
فقاعات وير وَفيلان	Weaire-Phelan bubbles
إسفين	Wedge
إطار سلكي	Wire-frame
Z
متعدد وجوه نُطُقِيّ	Zonohedron