BS
All
Articles
Dictionary
Quotes
Map

Wikiwand ❤️ Wikipedia

PrivacyTerms
Zlatni rez

Zlatni rez

From Wikipedia, the free encyclopedia

Zlatni rez
HistorijaIzračunavanjePrikazi broja φ {\displaystyle \varphi } Također pogledajteReference i fusnoteDalje čitanjeVanjski linkovi

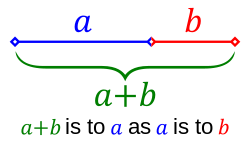
U matematici i umjetnosti, dvije veličine su u zlatnom rezu ako je omjer između sume te dvije veličine i veće od njih jednak sa odnosom veće veličine sa manjom veličinom. Zlatni rez je matematička konstanta, koja približno iznosi 1,6180339887.[1]

Thumb
Zlatni isječak je linijski segment prepolovljen na dva dijela prema pravilčima zlatnog reza. Ukupna dužina a + b je većem segmentu a isto što je a kraćem segmentu b.

Najkasnije od Renesanse, mnogi umjetnici i arhitekte su nastojali svoje radove praviti prema pravilima zlatnog reza, posebno u obliku zlatnog pravougaonika, u kojem je omjer duže stranice naspram dužine kraće stranice zlatni rez, a vjerovalo se da je ova proporcija estetski zadovoljavajuća. Matematičari su proučavali zlatni rez zbog njegovih jedinstvenih i interesantnih osobina.

Zlatni rez se često označava sa grčkim slovom ϕ (fi). Izgled zlatnog isječka ilustrira geometrijsku vezu koja definiše ovu konstantu. Izraženo algebarski:

a + b a = a b = φ . {\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}=\varphi \,.} {\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}=\varphi \,.}

Ova jednačina ima, kao jedinstveno, pozitivno rješenje, algebarsko iracionalan broj

φ = 1 + 5 2 ≈ 1.61803 39887 … {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.61803\,39887\ldots \,} {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.61803\,39887\ldots \,}[1]

Ostali nazivi, koji se koriste za ili za zlatnom rezu srodne pojmove, su zlatni isječak (latinski: sectio aurea), zlatna sredina, zlatni broj i grčko slovo fi (ϕ).[2][3][4] Ostali termini, koji se susreću, jesu ekstremni i srednji omjer, medijalni isječak, božanska proporcija, požanski isječak (latinski: sectio divina), zlatna proporcija, zlatni omjer,[5], te Fidiasova sredina.[6][7][8]

Thumb
Konstrukcija zlatnog pravougaonika:
1. Konstruišite jedinični kvadrat (crveno).
2. Povucite liniju sa sredine jedne stranice u suprotan ugao.
3. Iskoristite tu liniju kao radijus kako bi nacrtali luk koji definiše dužu dimenziju pravougaonika.

Teorija zlatnog reza započeta je u antici, a svoj procvat imala je u renesansi kada su umjetnici, matematičari, fizičari i astrolozi tražili savršenstvo u kompozicijama poznatih struktura.

Herodot (484. - 424. pne) „Jedan egipatski svećenik govoreći o obliku Keopsove piramide spomenuo mi je da je kvadrat nad njezinom visinom jednak površini bočnog trougla“

Thumb

v = a 2 φ {\displaystyle v={\frac {a}{2}}{\sqrt {\varphi }}} {\displaystyle v={\frac {a}{2}}{\sqrt {\varphi }}}

b = a 2 φ + 2 {\displaystyle b={\frac {a}{2}}{\sqrt {\varphi +2}}} {\displaystyle b={\frac {a}{2}}{\sqrt {\varphi +2}}}

α = arctg ⁡ φ {\displaystyle \alpha =\operatorname {arctg} {\sqrt {\varphi }}} {\displaystyle \alpha =\operatorname {arctg} {\sqrt {\varphi }}}

β = arctg ⁡ φ 2 {\displaystyle \beta =\operatorname {arctg} {\sqrt {\frac {\varphi }{2}}}} {\displaystyle \beta =\operatorname {arctg} {\sqrt {\frac {\varphi }{2}}}}

Grčki kipar Fidije u V vijeku pne.. primijenio je zlatni rez u dizajnu svojih skulptura i gradnji Partenona.

Platon (grčki filozof, V. i IV. vijek pne.) u „Timoteju“ opisuje pet pravilnih geometrijskih tijela kao osnovu harmonične strukture svijeta. Zlatni rez igra ključnu ulogu u dimenzijama i oblikovanju nekih od ovih tijela.

Pitagorejci (oko 500. god.pne.) dolaze do jednog od najvažnijih otkrića u matematici: - dijagonala i stranica kvadrata ( pravilnog peteugla) su nesamjerljive

Thumb

d a 5 = φ {\displaystyle {\frac {d}{a_{5}}}=\varphi } {\displaystyle {\frac {d}{a_{5}}}=\varphi }

Grčki matematičar Euklid prvi je ovaj broj uočio i matematički izrazio. Oko 300 godina prije Krista napisao je knjigu „Elementi“ u kojoj navodi prvu zabilježenu definiciju zlatnog reza.

Datu dužinu podijeliti tako da pravougaonik obuhvaćen cijelom dužinom i jednim odsječkom,bude jednak kvadratu na drugom odsječku.

a ( a − x ) = x 2 {\displaystyle a(a-x)=x^{2}} {\displaystyle a(a-x)=x^{2}}

x 2 + a x − a 2 = 0 {\displaystyle x^{2}+ax-a^{2}=0} {\displaystyle x^{2}+ax-a^{2}=0}

x = − 1 + 5 2 a {\displaystyle x={\frac {-1+{\sqrt {5}}}{2}}a} {\displaystyle x={\frac {-1+{\sqrt {5}}}{2}}a}

Sva znanja starih Grka objedinio je rimski arhitekt Marko Vitruvije u djelu De architectura libri decem ili Deset knjiga o arhitekturi, posvećenom imperatoru Augustu. Pisao je o simetriji hramova, a njihove proporcije upoređuje s razmjerima čovječijeg tijela. Vitruvije je ucrtao ljudsko tijelo u kružnicu, što je kasnije ponovo interpretirao Leonardo Da Vinci

Fra Luca Pacioli (1446–1510) štampao je u Veneciji 1509. djelo De divina proportione, koje je imalo veliki uticaj i nakon kojeg zlatni rez doživljava pravu renesansu. U njemu opisuje harmonijske osobine “božanske razmjere". Knjigu je ilustrirao Leonardo da Vinci.

Martin Ohm 1835. g. u drugom izdanju udžbenika Die reine Elementar -Mathematik ( Čista elementarna matematika) prvi put koristi termin zlatni rez.

Oznaku φ {\displaystyle \varphi } {\displaystyle \varphi } je 1909. predložio američki matematičar Mark Barr u čast slavnom starogrčkom kiparu Fidiji (Phidias 480–430. p. n. e.)

Spisak brojeva
γ - ζ(3) - √2 - √3 - √5 - φ - α - e - π - δ
Binarni 1.1001111000110111011...
Decimalni 1,6180339887498948482...
Heksadecimalni 1.9E3779B97F4A7C15F39...
Neprekidni razlomak 1 + 1 1 + 1 1 + 1 1 + 1 ⋱ {\displaystyle 1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{\ddots }}}}}}}}} {\displaystyle 1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{\ddots }}}}}}}}}
Algebarski oblik 1 + 5 2 {\displaystyle {\frac {1+{\sqrt {5}}}{2}}} {\displaystyle {\frac {1+{\sqrt {5}}}{2}}}

Za dvije veličine (pozitivni brojevi) a i b se kaže da su u zlatnom rezu ϕ ako vrijedi

a + b a = a b = φ . {\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}=\varphi \,.} {\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}=\varphi \,.}

Ova jednačina jednoznačno definiše ϕ.

Desna jednačina pokazuje da je a = bϕ, što se može zamijeniti u lijevi dio, dajući

b φ + b b φ = b φ b . {\displaystyle {\frac {b\varphi +b}{b\varphi }}={\frac {b\varphi }{b}}\,.} {\displaystyle {\frac {b\varphi +b}{b\varphi }}={\frac {b\varphi }{b}}\,.}

Poništavanjem b na obe strane, dobijamo

φ + 1 φ = φ . {\displaystyle {\frac {\varphi +1}{\varphi }}=\varphi .} {\displaystyle {\frac {\varphi +1}{\varphi }}=\varphi .}

Množenjem obe strane sa ϕ i premještanjem članova vodi do:

φ 2 − φ − 1 = 0. {\displaystyle {\varphi }^{2}-\varphi -1=0.} {\displaystyle {\varphi }^{2}-\varphi -1=0.}

Jedino pozitivno rješenje ove kvadratne jednačine je

φ = 1 + 5 2 ≈ 1.61803 39887 … {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.61803\,39887\dots \,} {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.61803\,39887\dots \,}

φ = 1 + 5 2 = 1,618 033988... {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=1{,}618033988...} {\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=1{,}618033988...}

1 + 1 φ = φ − 1 = 0.618033988... {\displaystyle {\frac {1+{\sqrt {1}}}{\varphi }}=\varphi -1=0.618033988...} {\displaystyle {\frac {1+{\sqrt {1}}}{\varphi }}=\varphi -1=0.618033988...}

φ 2 = φ + 1 {\displaystyle \varphi ^{2}=\varphi +1} {\displaystyle \varphi ^{2}=\varphi +1}

φ = 1 + φ = 1 + 1 + φ {\displaystyle \varphi ={\sqrt {1+\varphi }}={\sqrt {1+{\sqrt {1+\varphi }}}}} {\displaystyle \varphi ={\sqrt {1+\varphi }}={\sqrt {1+{\sqrt {1+\varphi }}}}}

φ = 1 + 1 + 1 . . . {\displaystyle \varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1}}...}}}}} {\displaystyle \varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1}}...}}}}}

φ = 1 + 1 φ = 1 + 1 1 + 1 φ = . . . {\displaystyle \varphi =1+{\frac {1}{\varphi }}=1+{\frac {1}{1+{\frac {1}{\varphi }}}}=...} {\displaystyle \varphi =1+{\frac {1}{\varphi }}=1+{\frac {1}{1+{\frac {1}{\varphi }}}}=...}

φ = 1 + 1 1 + 1 1 + 1 1 + 1 1 + . . . {\displaystyle \varphi =1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+...}}}}}}}}} {\displaystyle \varphi =1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+...}}}}}}}}}

φ = 1 + 1 + 1 + 1 + ⋯ {\displaystyle \varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\cdots }}}}}}}}} {\displaystyle \varphi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\cdots }}}}}}}}}

  • Estetika
  • Zlatni ugao
  • Zlatna funkcija
  • Zlatni pravougaonik
  • Zlatni teougao (matematika)
  • Traženje zlatnog isječka
  • Fi
  • Keplerov trougao
  • Logaritamska spirala
  • Fibonaccijev broj
  • Modulor
  • Sveta geometrija
  • Ruže Heliogabalusa
  • Plastični broj
  • Penroseovo popločanje
  • Dinamička simetrija
  • Baza zlatnog reza
  • Vitruvijev čovjek
  • Kvadratni korijen od 5
  • Srebrni rez
  • Spisak radova dizajniranih sa zlatnim rezom
  1. [1]
    The golden ratio can be derived by the quadratic formula, by starting with the first number as 1, then solving for 2nd number x, where the ratios (x + 1)/x = x/1 or (multiplying by x) yields: x + 1 = x2, or thus a quadratic equation: x2 − x − 1 = 0. Then, by the quadratic formula, for positive x = (−b + √(b2 − 4ac))/(2a) with a = 1, b = −1, c = −1, the solution for x is: (−(−1) + √((−1)2 − 4·1·(−1)))/(2·1) or (1 + √(5))/2.
  2. [2]
    Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
  3. [3]
    Piotr Sadowski, The Knight on His Quest: Symbolic Patterns of Transition in Sir Gawain and the Green Knight, Cranbury NJ: Associated University Presses, 1996
  4. [4]
    Richard A Dunlap, The Golden Ratio and Fibonacci Numbers, World Scientific Publishing, 1997
  5. [5]
    Summerson John, Heavenly Mansions: And Other Essays on Architecture (New York: W.W. Norton, 1963) pp.37 . "And the same applies in architecture, to the rectangles representing these and other ratios (e.g. the 'golden cut'). The sole value of these ratios is that they are intellectually fruitful and suggest the rhythms of modular design."
  6. [6]
    Jay Hambidge, Dynamic Symmetry: The Greek Vase, New Haven CT: Yale University Press, 1920
  7. [7]
    William Lidwell, Kritina Holden, Jill Butler, Universal Principles of Design: A Cross-Disciplinary Reference, Gloucester MA: Rockport Publishers, 2003
  8. [8]
    Pacioli, Luca. De divina proportione, Luca Paganinem de Paganinus de Brescia (Antonio Capella) 1509, Venice.
  • Doczi, György (2005) [1981]. The Power of Limits: Proportional Harmonies in Nature, Art, and Architecture. Boston: Shambhala Publications. ISBN 1-590-30259-1. CS1 održavanje: nepreporučeni parametar (link)
  • Huntley, H. E. (1970). The Divine Proportion: A Study in Mathematical Proportion. New York: Dover Publications. ISBN 0-486-22254-3. CS1 održavanje: nepreporučeni parametar (link)
  • Arakelyan, Hrant. Mathematics and Hstory of the Golden Section. – Logos 2014, 404 p. — ISBN 978-5-98704-663-0, (rus.).
  • Joseph, George G. (2000) [1991]. The Crest of the Peacock: The Non-European Roots of Mathematics (New Ed. izd.). Princeton, NJ: Princeton University Press. ISBN 0-691-00659-8. |edition= sadrži dodatni tekst (pomoć)CS1 održavanje: nepreporučeni parametar (link)
  • Sahlqvist, Leif (2008). Cardinal Alignments and the Golden Section: Principles of Ancient Cosmography and Design (3rd Rev. Ed. izd.). Charleston, SC: BookSurge. ISBN 1-4196-2157-2. |edition= sadrži dodatni tekst (pomoć)CS1 održavanje: nepreporučeni parametar (link)
  • Schneider, Michael S. (1994). A Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and Science. New York: HarperCollins. ISBN 0-060-16939-7. CS1 održavanje: nepreporučeni parametar (link)
  • Walser, Hans (2001) [Der Goldene Schnitt 1993]. The Golden Section. Peter Hilton trans. Washington, DC: The Mathematical Association of America. ISBN 0-88385-534-8. CS1 održavanje: nepreporučeni parametar (link)
Logo Commonsa
Logo Commonsa
Zlatni rez na Wikimedia Commonsu.
  • Green, Thomas M. (updated June 20, 2005). "The Pentagram & The Golden Ratio". Arhivirano s originala, 5. 11. 2007. Nepoznati parametar |accessyear= zanemaren (prijedlog zamjene: |access-date=) (pomoć); Nepoznati parametar |accessmonthday= zanemaren (pomoć); Provjerite vrijednost datuma u parametru: |date= (pomoć)CS1 održavanje: nepreporučeni parametar (link) Geometry instruction with problems to solve.
  • Khan, Amore (revised February 2, 2007). "Khan Amore's Commentary on the Divine Proportion". Arhivirano s originala (HTML; PDF available), 7. 4. 2009. Pristupljeno 29. 12. 2008. Nepoznati parametar |accessyear= zanemaren (prijedlog zamjene: |access-date=) (pomoć); Nepoznati parametar |accessmonthday= zanemaren (pomoć); Provjerite vrijednost datuma u parametru: |date= (pomoć)CS1 održavanje: nepreporučeni parametar (link)
  • Knott, Ron. "The Golden section ratio: Phi". Arhivirano s originala, 5. 12. 2006. Pristupljeno 29. 12. 2008. CS1 održavanje: nepreporučeni parametar (link) Information and activities by a mathematics professor.
  • Eric W. Weisstein, Zlatni rez na MathWorld-u.
  • Irlande, Alexis. "The golden number to 17 000 000 000 digits". Arhivirano s originala, 6. 1. 2010. Pristupljeno 29. 12. 2008. Nepoznati parametar |accessyear= zanemaren (prijedlog zamjene: |access-date=) (pomoć); Nepoznati parametar |accessmonthday= zanemaren (pomoć); Referenca sadrži prazan nepoznati parametar: |month= (pomoć)CS1 održavanje: nepreporučeni parametar (link)
  • "Golden Section" by Michael Schreiber, Wolfram Demonstrations Project, 2007.
  • http://normala.hr/prezentacije/mkabic/zlatnirez/ZlatniRez.pdf%5B%5D
  • Zlatni rez u radovima slikara Alfreda F. Krupe
Edit in WikipediaRevision historyRead in Wikipedia

Wikiwand in your browser!

Seamless Wikipedia browsing. On steroids.

Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.

Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.

Chrome
Wikiwand for Chrome
Edge
Wikiwand for Edge
Firefox
Wikiwand for Firefox

Historija

Izračunavanje

Prikazi broja φ {\displaystyle \varphi }

Također pogledajte

Reference i fusnote

Dalje čitanje

Vanjski linkovi