Forat de cuc

En física, un forat de cuc, també conegut com un pont EPR=KOI, és una hipotètica característica topològica d'un espaitemps, descrita per les equacions de la relativitat general, la qual és essencialment «una drecera» a través de l'espai i el temps. Un forat de cuc té com a mínim dos extrems, els quals estan connectats per una única «gola», fent que la matèria es pugui «desplaçar» d'un extrem a l'altre a través d'aquesta. Avui dia encara no s'ha descobert cap prova que l'espaitemps conegut contingui estructures d'aquest tipus, és a dir, els forats de cuc són una hipòtesi.

Esquema d'un forat de cuc que permet, tècnicament, el viatge a través del temps. Si un dels dos extrems del pont és travessat per la línia verda, està en moviment, segueix la ruta vermella i torna al punt inicial amb el sentit oposat a la ruta verda podria permetre tornar enrere en el temps, ja que l'espaitemps representat tindria corbes temporals tancades

El primer científic a advertir d'aquesta teoria fou Ludwig Flamm l'any 1916. En aquest sentit, la hipòtesi del forat de cuc és una actualització de la vuitcentista teoria d'una quarta dimensió espacial que suposa -per exemple-, donat un cos torodial en què es podrien trobar, les tres dimensions espacials perceptibles i una quarta dimensió espacial que abreujaria les distàncies i també els temps de viatge. Aquesta primera noció va ser plasmada més científicament l'any 1921 pel matemàtic Hermann Weyl, en relació amb les seves anàlisis de la massa en termes de l'energia d'un camp electromagnètic a partir de la teoria relativista d'Albert Einstein publicada l'any 1916.

Avui en dia, la teoria de cordes admet l'existència de més de tres dimensions espacials (veure hiperespai), però les altres dimensions espacials estarien contretes o compactades a escales subatòmiques (segons la teoria de Kaluza-Klein), i pel que sembla seria molt difícil o «impossible» aprofitar aquestes dimensions espacials per a realitzar viatges en l'espaitemps.

Origen del nom

El terme forat de cuc fou introduït pel físic teòric americà John Wheeler el 1957 (inspirat a l'obra d'Hermann Weyl) i mitjançant un article coescrit amb Charles Misner:^[1]

«	Aquesta anàlisi obliga a considerar situacions ... on hi ha un flux net de línies de força, a través del que els topòlegs dirien "descomposició toroidal" de l'espai amb múltiples connexions, i quines els físics tal vegada podrien excusar-se per a denominar més vívidament un "forat de cuc".	»
— Charles Misner i John Wheeler a Annals of Physics

Prové de la següent analogia usada per a explicar el fenomen: si l'univers és la pell d'una poma, i un cuc viatja sobre la seva superfície, la distància d'un punt de la poma al seu antípoda és igual a la meitat de la circumferència de la poma, sempre que el cuc romangui sobre la superfície d'aquesta. Però si en comptes d'això, el cuc cavés un forat directament a través de la poma, la distància que hauria de recórrer seria considerablement menor, ja que la distància més pròxima entre dos punts és una línia recta que uneix a tots dos.

Tipus de forat de cuc

• Els forats de cuc de l'intraunivers connecten una posició d'un univers amb una altra posició del mateix univers en un temps diferent. Un forat de cuc hauria de poder connectar posicions distants en l'univers per plegaments espaciotemporals, de manera que permetria viatjar entre elles en un temps menor que el que prendria fer el viatge a través de l'espai normal.
• Els forats de cuc de l'interunivers associen un univers amb un altre diferent i es denominen «forats de cuc de Schwarzschild». Això permet especular sobre si tals forats de cuc podrien usar-se per a viatjar d'un univers a un altre paral·lel. Una altra aplicació d'un forat de cuc podria ser el viatge en el temps. En aquest cas, seria una drecera per a desplaçar-se d'un punt espaciotemporal a un altre. En la teoria de cordes, un forat de cuc és vist com la connexió entre dues D-branes, on les boques estan associades a les branas i connectades per un tub de flux. Es creu que els forats de cuc són una part de l'escuma quàntica o espaciotemporal.

Una altra classificació:

• Els forats de cuc euclidians, estudiats en física de partícules.
• Els forats de cuc de Lorentz, principalment estudiats en relativitat general i en gravetat semiclàssica. Dins d'aquests destaquen els forats de cuc travessables, un tipus especial de forat de cuc de Lorentz que permetria a un ésser humà viatjar d'un costat a l'altre del forat.

Fins al moment s'ha teoritzat sobre diferents tipus de forats de cuc, principalment com a solucions matemàtiques a la qüestió. Essencialment, aquests tipus de forat de cuc són:

• El forat de cuc de Schwarzschild suposadament format per un forat negre de Schwarzschild, que es considera infranquejable.
• El forat de cuc suposadament format per un forat negre de Reissner-Nordstrøm o Kerr-Newman, que resultaria franquejable, però en una sola direcció, i que podria contenir un forat de cuc de Schwarzschild.
• El forat de cuc de Lorentz, que posseeix massa negativa i s'estima franquejable en totes dues direccions (passat i futur).

Forats de cuc de Schwarzschild

Diagrama d'un forat de cuc de Schwarzschild.

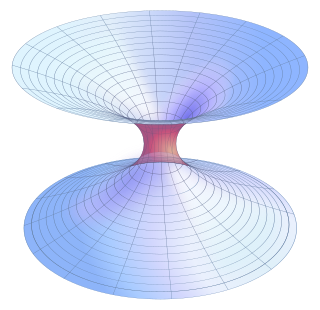
Els forats de cuc de Lorentz, coneguts com a forats de cuc de Schwarzschild o ponts d'Einstein-Rosen, són nexes que uneixen àrees d'espai que pot ser modelades com a solucions de buit en les equacions de camp d'Einstein per unió d'un model de forat negre i un de forat blanc. Aquesta solució va ser trobada per Albert Einstein i el seu company Nathan Rosen, que va publicar primer el resultat en 1935. No obstant això, en 1962, John A. Wheeler i Robert W. Fuller van publicar un article en el qual divulgaven la demostració que aquest tipus de forat de cuc és inestable i es desintegraria instantàniament tan aviat com es formés.

Abans que els problemes d'estabilitat dels forats de cuc de Schwarzschild es fessin evidents, es va proposar que els quàsars podien ser forats blancs, de manera que formaven les zones terminals dels forats de cuc d'aquest tipus. No obstant això, recerques recents descarten que els quàsars siguin equiparables als forats blancs.

Els forats de cuc de Schwarzschild van inspirar a Kip Thorne a imaginar el trànsit per ells mitjançant la subjecció de la seva gola i la seva obertura per mitjà de matèria exòtica (de massa i energia negativa).

Forats de cuc practicables

Imatge d'un forat de cuc practicable (que es pot travessar) que connectaria l'àrea enfront de l'institut de física de la Universitat de Tubinga amb les dunes pròximes a Boulogne-sur-Mer, en el nord de França. La imatge ha estat recreada mitjançant un programari de traçat de raigs en 4D, en una mètrica de Morris-Thorne, encara que els efectes gravitatoris sobre la longitud d'ona no s'han simulat.^[2]

Els forats de cuc practicables de Lorentz, també anomenats travessables, permetrien viatjar no sols d'una part de l'Univers a una altra, sinó fins i tot d'un univers a un altre. Els forats de cuc connecten dos punts de l'espaitemps, per la qual cosa permetrien el viatge tant en l'espai com en el temps. En la teoria de la relativitat general, la possibilitat de travessar forats de cuc va ser demostrada per primera vegada per Kip S. Thorne i el seu graduat Mike Morris en un article publicat en 1988. El tipus de forat de cuc travessable que ells van descobrir es mantindria obert per una espècie de petxina esfèrica de matèria exòtica denominada forat de cuc de Morris-Thorne. Posteriorment, s'han descobert altres tipus de forats de cuc travessables, com un que es manté obert per cordes còsmiques, ja hipotetitzat abans per Matt Visser en un article publicat en 1989.

Base teòrica

Analogia 2D amb un forat de cuc (pont d'Einstein-Rosen). (a) camí llarg a través de l'espai normal (magenta) (b) camí curt a través del forat de cuc (verd)

Definició

La definició topològica de forat de cuc no és gens intuïtiva. Es diu que en una regió compacta de l'espaitemps existeix un forat de cuc quan el seu conjunt frontera és trivial des del punt de vista topològic, però el seu interior no és simplement connex. Formalitzar aquesta idea condueix a definicions com la següent, presa del Lorentzian Wormholes, de Matt Visser:

Si un espaitemps de Lorentz conté una regió compacta Ω i si la topologia de Ω és de la forma Ω ~ R x Σ, on Σ és una 3-varietat de topologia no trivial, que la seva frontera té topologia de la forma dΣ ~ S², i si a més les hipersuperfícies Σ són de tipus espacial, llavors la regió Ω conté un forat de cuc intrauniversal quasipermanent.

Caracteritzar forats de cuc de l'interunivers és més difícil. Per exemple, podem imaginar un univers nounat connectat al seu progenitor per un melic estret. Caldria considerar el melic com la gola d'un forat de cuc, per la qual l'espaitemps està connectat.

Plausibilitat

Es coneix que els forats de cuc de Lorentz són possibles dins de la relativitat general, però la possibilitat física d'aquestes solucions és incerta. Fins i tot, es desconeix si la teoria de la gravetat quàntica, que s'obté en condensar la relativitat general amb la mecànica quàntica, permetria l'existència d'aquests fenòmens. La majoria de les solucions conegudes de la relativitat general que permeten l'existència de forats de cuc travessats requereixen l'existència de matèria estranya, una substància teòrica que conté energia de densitat negativa. No obstant això, no ha estat matemàticament provat que aquest sigui un requisit absolut per a aquest tipus forats de cuc travessats ni s'ha establert que la matèria exòtica no pot existir.

Encara no se sap empíricament si existeixen forats de cuc. Una solució a les equacions de la relativitat general (tal com la que trobés L. Flamm) que fes possible l'existència d'un forat de cuc sense el requisit d'una matèria exòtica —substància teòrica que posseiria una densitat d'energia negativa— no ha estat encara verificada. Molts físics, inclòs Stephen Hawking (amb el seu conjectura de protecció cronològica), consideren que a causa de les paradoxes (o potser apories) un viatge en el temps a través d'un forat de cuc implicaria que existís una cosa fonamental en les lleis de la física que impedeixi tals fenòmens (vegeu censura còsmica).

El març de 2005, Amos Ori va visualitzar un forat de cuc que permetia viatjar en el temps sense requerir matèria exòtica i satisfent totes les condicions energètiques. L'estabilitat d'aquesta solució és incerta, per la qual cosa segueix sense quedar clar si es requeriria una precisió infinita perquè es formés i permetés el viatge en el temps i si els efectes quàntics protegirien la seqüència cronològica del temps en aquest cas.

Mètrica dels forats de cuc

Les teories sobre la mètrica dels forats de cuc descriuen la geometria de l'espaitemps d'un forat de cuc i serveixen de models teòrics per al viatge en el temps. Un exemple simple de la mètrica d'un forat de cuc travessat podria ser el següent:^[3]

${\displaystyle ds^{2}=-c^{2}{\text{d}}t^{2}+{\text{d}}l^{2}+(k^{2}+l^{2})({\text{d}}\theta ^{2}+\sin ^{2}\theta \,{\text{d}}\phi ^{2})}$

Un tipus de mètrica de forat de cuc no travessat és la solució de Schwarzschild:

${\displaystyle ds^{2}=-\left(1-{\frac {2GM}{c^{2}r}}\right){\text{d}}t^{2}+{\frac {{\text{d}}r^{2}}{1-{\cfrac {2GM}{c^{2}r}}}}+r^{2}({\text{d}}\theta ^{2}+\sin ^{2}\theta \,{\text{d}}\phi ^{2})}$

representat per primera vegada per Ellis com un cas especial de drenatge de Ellis.

El pont d'Einstein-Rosen es va descriure en un article publicat el juliol de 1935.^[4][5]

Per a la solució estàtica simètricament esfèrica de Schwarzschild.

${\displaystyle ds^{2}=-{\frac {1}{1-{\frac {2m}{r}}}}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2})+(1-{\frac {2m}{r}})dt^{2}}$

(${\displaystyle ds}$ = moment adequat, ${\displaystyle c}$ = 1)

Si un reemplaça ${\displaystyle r}$ per ${\displaystyle u}$ segons ${\displaystyle u^{2}=r-2m}$

L'espai de quatre dimensions es descriu matemàticament mitjançant dues parts congruents o "fulles", que corresponen a ${\displaystyle u}$ > 0 i ${\displaystyle u}$ < 0, que estan unides per un hiperplà ${\displaystyle r=2m}$ o ${\displaystyle u}$ = 0 en el que ${\displaystyle g}$ desapareix. Anomenem a tal connexió entre les dues fulles un "pont" (autors: A. Einstein, N. Rosen, "The Particle Problem in the General Theory of Relativity")

Per a la combinació gravetat i electricitat, Einstein i Rosen van derivar la solució esfèrica simètrica de Schwarzschild

${\displaystyle \phi _{1}=\phi _{2}=\phi _{3}=0,\phi _{4}={\frac {\epsilon }{4}},}$

${\displaystyle ds^{2}=-{\frac {1}{(1-{\frac {2m}{r}}-{\frac {\epsilon ^{2}}{2r^{2}}})}}dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2})+(1-{\frac {2m}{r}}-{\frac {\epsilon ^{2}}{2r^{2}}})dt^{2}}$

(${\displaystyle \epsilon }$ = càrrega elèctrica)

Les equacions de camp sense denominadors en el cas que ${\displaystyle m}$ = 0 es poden escriure

${\displaystyle \phi _{\mu \nu }=\phi _{\mu ,\nu }-\phi _{\nu ,\mu }}$

${\displaystyle g^{2}\phi _{\mu \nu$ ;\sigma }g^{\nu \sigma }=0}

${\displaystyle g^{2}(R_{ik}+\phi _{i\alpha }\phi _{k}^{\alpha }-{\frac {1}{4}}g_{ik}\phi _{\alpha \beta }\phi ^{ab})=0}$

Per eliminar les singularitats, si es reemplaça ${\displaystyle r}$ per ${\displaystyle u}$ segons l'equació:

${\displaystyle u^{2}=r^{2}-{\frac {\epsilon ^{2}}{2}}}$

i amb ${\displaystyle m}$ = 0 s'obté^[6][7]

${\displaystyle \phi _{1}=\phi _{2}=\phi _{3}=0,\phi _{4}=\epsilon /(u^{2}+{\frac {\epsilon ^{2}}{2}})^{\frac {1}{2}}}$

${\displaystyle ds^{2}=-du^{2}-(u^{2}+{\frac {\epsilon ^{2}}{2}})(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2})+({\frac {2u^{2}}{2u^{2}+\epsilon ^{2}}})dt^{2}}$

La solució està lliure de singularitats per a tots els punts finits a l'espai de les dues fulles (autors: A. Einstein, N. Rosen, "The Particle Problem in the General Theory of Relativity")

Viatges en el temps

Un forat de cuc podria permetre en teoria el viatge en el temps. Això es podria dur a terme accelerant l'extrem final d'un forat de cuc a una velocitat relativament alta respecte al seu altre extrem. La dilatació de temps relativista resultaria en una boca del forat de cuc accelerada envellint més lentament que la boca estacionària, vist per un observador extern, de manera semblant al que s'observa en la paradoxa dels bessons. No obstant això, el temps passa diferentment a través del forat de cuc respecte de l'exterior, per la qual cosa els rellotges sincronitzats en cada boca romandran sincronitzats per algú que viatja a través del forat de cuc, sense importar com es moguin les boques. Això vol dir que qualsevol cosa que entri per la boca accelerada del forat de cuc podria sortir per la boca estacionària en un punt temporal anterior al de la seva entrada si la dilatació de temps ha estat suficient.