Doppelpyramide

Eine ${\displaystyle n}$-eckige Doppelpyramide (auch Bipyramide oder Dipyramide, englisch dipyramid) ist ein Polyeder, das entsteht, indem man eine ${\displaystyle n}$-eckige Pyramide und ihr Spiegelbild an den Grundflächen verklebt. Das ${\displaystyle n}$-Eck, das die gemeinsame Grundfläche der beiden Pyramiden darstellt, ist keine Seitenfläche der Doppelpyramide, sondern liegt im Inneren der Doppelpyramide, in der Symmetrieebene zwischen den beiden ${\displaystyle n}$-eckigen Pyramiden. Die Doppelpyramide hat damit ${\displaystyle 2}$ Spitzen, ${\displaystyle 2+n}$ Ecken und ${\displaystyle 3\cdot n}$ Kanten und ihre Oberfläche besteht aus ${\displaystyle 2\cdot n}$ Dreiecken.

Doppelpyramide mit einem Sechseck als Grundfläche

Besondere Doppelpyramiden

Nur drei Arten von Doppelpyramiden haben die Eigenschaft, dass alle Kanten dieselbe Länge haben können, sodass alle Seitenflächen gleichseitige Dreiecke sind: die dreieckige, die viereckige und die fünfeckige Doppelpyramide. Diese spezielle viereckige Doppelpyramide, das Oktaeder, zählt zu den platonischen Körpern, während die dreieckige und die fünfeckige Doppelpyramide zu den Johnson-Körpern zählen (J12 und J13). Diese drei Doppelpyramiden sind Deltaeder.

Regelmäßige Doppelpyramide

Von einer regelmäßigen Doppelpyramide spricht man, wenn die erzeugende Pyramide regelmäßig ist, d. h. wenn deren Grundfläche ein regelmäßiges Vieleck ist und die Gerade durch die Doppelpyramidenspitzen die Grundfläche senkrecht schneidet.

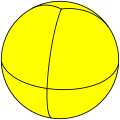
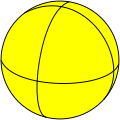
Eine regelmäßige Doppelpyramide kann auf eine solche Weise auf die Sphäre bzw. eine Kugel projiziert werden, dass ihre Spitzen auf zwei sich gegenüberliegende Punkte (die Pole) auf der Kugel abgebildet werden, das regelmäßige ${\displaystyle n}$-Eck auf den Äquator um die Achse durch die beiden Pole und die an den Doppelpyramidenspitzen anliegenden Kanten in gleichabständige Längenkreise durch die Pole, die den Äquator jeweils senkrecht schneiden. Die Seitenflächen der Doppelpyramide werden dabei auf sphärische Dreiecke abgebildet.

Die Symmetriegruppe einer regelmäßigen Doppelpyramide ist das direkte Produkt ihrer Drehgruppe mit der zweielementigen Gruppe, die von der Spiegelung an der Ebene senkrecht zur Drehachse erzeugt wird. Die Symmetriegruppe der regelmäßigen, ${\displaystyle n}$-eckigen Doppelpyramide ist ${\displaystyle D_{nh}}$ der Ordnung ${\displaystyle 4\cdot n}$ außer im Fall des Oktaeders, dessen Symmetriegruppe die Oktaedergruppe ${\displaystyle O_{h}}$ der Ordnung 48 ist. Die Drehgruppe einer regelmäßigen Doppelpyramide ist die Diedergruppe ${\displaystyle D_{n}}$ der Ordnung ${\displaystyle 2\cdot n}$ außer im Fall des Oktaeders, dessen Drehgruppe Oktaedergruppe ${\displaystyle O}$ der Ordnung 24 ist (isomorph zur symmetrischen Gruppe ${\displaystyle S_{4}}$ auf der Menge der Raumdiagonalen, also zur Gruppe der ${\displaystyle 4!=24}$ Permutationen der vier Raumdiagonalen).

3	4	5	6	7	8	9	10

Formeln

Größen einer regelmäßigen Doppelpyramide (regelmäßiges n-Eck mit Seitenlänge a als Grundfläche und Höhe a)
	Allgemeiner Fall	Quadratische Doppelpyramide (Spezialfall n = 4)	Regelmäßige Dreiecks-Doppelpyramide (Spezialfall n = 3)
Volumen	${\displaystyle V={\frac {n\cdot a^{2}\cdot h}{6}}\cdot \cot \left({\frac {\pi }{n}}\right)}$	${\displaystyle V={\frac {2\cdot a^{2}\cdot h}{3}}}$	${\displaystyle V={\frac {a^{2}\cdot h}{6}}\cdot {\sqrt {3}}}$
Oberflächeninhalt	${\displaystyle A={\frac {n\cdot a}{2}}\cdot {\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}}$	${\displaystyle A=2\cdot a\cdot {\sqrt {4\cdot h^{2}+a^{2}}}}$	${\displaystyle A={\frac {3\cdot a}{2}}\cdot {\sqrt {4\cdot h^{2}+{\frac {a^{2}}{3}}}}}$
Steilkantenlänge	${\displaystyle l=\left(h^{2}+{\frac {a^{2}}{4\cdot \sin ^{2}\left({\frac {\pi }{n}}\right)}}\right)^{\frac {1}{2}}}$	${\displaystyle l={\sqrt {h^{2}+{\frac {a^{2}}{2}}}}}$	${\displaystyle l={\sqrt {h^{2}+{\frac {a^{2}}{3}}}}}$
Inkugelradius	${\displaystyle r_{i}={\frac {a\cdot h}{\sqrt {a^{2}+4\cdot h^{2}\cdot \tan ^{2}\left({\frac {\pi }{n}}\right)}}}}$	${\displaystyle r_{i}={\frac {a\cdot h}{\sqrt {a^{2}+4\cdot h^{2}}}}}$	${\displaystyle r_{i}={\frac {a\cdot h}{\sqrt {a^{2}+12\cdot h^{2}}}}}$
Innenwinkel der regelmäßigen Grundfläche	${\displaystyle \alpha ={\frac {n-2}{n}}\cdot 180^{\circ }}$	${\displaystyle \alpha =90^{\circ }}$	${\displaystyle \alpha =60^{\circ }}$
Basiswinkel der gleichschenkligen Dreiecke	${\displaystyle \alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}\cdot {\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}\right)}$	${\displaystyle \alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}\cdot {\sqrt {4\cdot h^{2}+a^{2}}}\right)}$	${\displaystyle \alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}\cdot {\sqrt {4\cdot h^{2}+{\frac {a^{2}}{3}}}}\right)}$
Innenwinkel an der Spitze der gleichschenkligen Dreiecke	${\displaystyle \alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}}\right)}$	${\displaystyle \alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+a^{2}}}}\right)}$	${\displaystyle \alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+{\frac {a^{2}}{3}}}}}\right)}$
Diederwinkelzwischen Grundfläche und gleichschenkligen Dreiecken	${\displaystyle \beta _{1}=\arctan \left({\frac {2\cdot h\cdot \tan \left({\frac {\pi }{n}}\right)}{a}}\right)}$	${\displaystyle \beta _{1}=\arctan \left({\frac {2\cdot h}{a}}\right)}$	${\displaystyle \beta _{1}=\arctan \left({\frac {2\cdot {\sqrt {3}}\cdot h}{a}}\right)}$
Diederwinkel zwischen den gleichschenkligen Dreiecken	${\displaystyle \beta _{2}=2\cdot \arctan \left({\frac {1}{2\cdot h}}\cdot \left({\frac {4\cdot h^{2}\cdot \sin ^{2}\left({\frac {\pi }{n}}\right)+a^{2}}{\tan ^{2}\left({\frac {\pi }{n}}\right)-\sin ^{2}\left({\frac {\pi }{n}}\right)}}\right)^{\frac {1}{2}}\right)}$	${\displaystyle \beta _{2}=2\cdot \arctan \left({\frac {1}{2\cdot h}}\cdot {\sqrt {4\cdot h^{2}+2\cdot a^{2}}}\right)}$	${\displaystyle \beta _{2}=2\cdot \arctan \left({\frac {1}{3\cdot h}}\cdot {\sqrt {3\cdot h^{2}+a^{2}}}\right)}$
Raumwinkel am Äquator	${\displaystyle \Omega _{1}=8\cdot \arctan \left({\sqrt {\tan \left({\frac {2\cdot \alpha _{1}+\alpha }{4}}\right)\cdot \tan \left({\frac {2\cdot \alpha _{1}-\alpha }{4}}\right)\cdot \tan ^{2}\left({\frac {\alpha }{4}}\right)}}\right)}$
Raumwinkel in der Spitze	${\displaystyle {\begin{aligned}\Omega _{2}&=4\cdot n\cdot \arctan \left({\sqrt {\tan \left({\frac {2\cdot \gamma _{2}+\alpha _{3}}{4}}\right)\cdot \tan \left({\frac {2\cdot \gamma _{2}-\alpha _{3}}{4}}\right)\cdot \tan ^{2}\left({\frac {\alpha _{3}}{4}}\right)}}\right)\\&=2\cdot \pi -2\cdot n\cdot \arcsin \left(\cos \left({\frac {\pi }{n}}\right)\cdot {\sqrt {\tan ^{2}\left({\frac {\pi }{n}}\right)-\tan ^{2}\left({\frac {\alpha _{3}}{2}}\right)}}\right)\\\end{aligned}}}$

Bemerkungen: Für die Herleitung der meisten Formeln werden der Satz des Pythagoras, Sätze für trigonometrischen Funktionen und Sätze für den Arkustangens verwendet.

Der Raumwinkel in den Ecken der Grundfläche einer geraden regelmäßigen Pyramide, wo drei Seitenflächen (ein regelmäßiges ${\displaystyle n}$-Eck und zwei gleichschenklige Dreiecke) mit den Innenwinkeln ${\displaystyle \alpha }$, ${\displaystyle \alpha _{1}}$, ${\displaystyle \alpha _{1}}$ zusammentreffen, wird mit dem Satz von L’Huilier berechnet (siehe Raumwinkel - Kanten-Formel).^[1] Der Raumwinkel am Äquator der regelmäßigen Doppelpyramide ist wegen Spiegelsymmetrie zweimal so groß.

Der Raumwinkel in der Spitze, wo ${\displaystyle n}$ Seitenflächen zusammentreffen, kann auch mit dem Satz von L’Huilier berechnet werden, indem die regelmäßige Pyramide in ${\displaystyle n}$ nicht regelmäßige Tetraeder mit den Kantenlängen ${\displaystyle a}$, ${\displaystyle l}$, ${\displaystyle l}$, ${\displaystyle h}$, ${\displaystyle R_{u}}$, ${\displaystyle R_{u}}$ zerlegt wird, wobei ${\displaystyle R_{u}={\tfrac {a}{2\cdot \sin \left({\frac {\pi }{n}}\right)}}}$ der Umkreisradius der regelmäßigen Grundfläche ist. Dabei wird der Raumwinkel in der Spitze wegen Rotationssymmetrie in ${\displaystyle n}$ gleich große und kongruente Teilwinkel zerlegt. Also haben diese ${\displaystyle n}$ nicht regelmäßige Tetraeder dort eine gemeinsame Ecke. In dieser Ecke treffen jeweils drei Seitenflächen mit den Innenwinkeln ${\displaystyle \alpha _{3}}$, ${\displaystyle \gamma _{2}}$, ${\displaystyle \gamma _{2}}$ zusammen.

Eine andere Möglichkeit, den Raumwinkel in der Spitze zu berechnen, ist, die Formel von H. C. Rajpoot für den rotationssymmetrischen Ecken-Raumwinkel anzuwenden.^[2] Dabei müssen die Innenwinkel aller ${\displaystyle n}$ Seitenflächen, die in einer Ecke zusammentreffen, gleich groß sein, was für alle regelmäßigen Pyramiden und Doppelpyramiden der Fall ist.

Spezialfälle

Für bestimmte Werte von ${\displaystyle n}$ und ${\displaystyle h}$ ergeben sich Zusammenhänge mit platonischen Körpern oder Johnson-Körpern:

• Für ${\displaystyle n=3}$ und ${\displaystyle h={\frac {a}{3}}\cdot {\sqrt {6}}}$ ergibt sich die regelmäßige Dreiecks-Doppelpyramide mit gleichseitigen Dreiecken, der Johnson-Körper ${\displaystyle J_{12}}$. Sie besteht aus zwei regelmäßigen Tetraedern.
• Für ${\displaystyle n=4}$ und ${\displaystyle h={\frac {a}{2}}\cdot {\sqrt {2}}}$ ergibt sich die quadratische Doppelpyramide mit gleichseitigen Dreiecken, nämlich das Oktaeder.
• Für ${\displaystyle n=5}$ und ${\displaystyle h={\frac {a}{10}}\cdot {\sqrt {50-10\cdot {\sqrt {5}}}}}$ ergibt sich die regelmäßige Fünfecks-Doppelpyramide mit gleichseitigen Dreiecken, der Johnson-Körper ${\displaystyle J_{13}}$. Die beiden Hälften sind regelmäßige Pyramiden, die Teile des Ikosaeders sind.

• 
  Johnson-Körper ${\displaystyle J_{12}}$
• 
  Oktaeder
• 
  Johnson-Körper ${\displaystyle J_{13}}$

Gerade Doppelpyramide

Ist die Pyramide, die eine Doppelpyramide erzeugt, gerade, so spricht man von einer geraden Doppelpyramide. Der duale Körper einer geraden Doppelpyramide ist ein gerades Prisma und umgekehrt.

• 
  Der Würfel als Dual des Oktaeders
• 
  Das Oktaeder als Dual des Würfels

Allgemeine Doppelpyramide

Volumen

Blaw-Knox-Sendemast in Lakihegy, Ungarn, in Form einer Doppelpyramide

Das Volumen einer Doppelpyramide ist ${\displaystyle V={\tfrac {2}{3}}\cdot G\cdot h}$, wobei ${\displaystyle G}$ den Flächeninhalt der Grundfläche der erzeugenden Pyramide bezeichnet und ${\displaystyle h}$ die Höhe einer Spitze über dieser Grundfläche. Diese Formel gilt unabhängig davon, ob es sich um eine gerade Doppelpyramide handelt oder nicht, solange die Höhe ${\displaystyle h}$ als der orthogonale Abstand einer Spitze zur Ebene, in der die Grundfläche liegt, bestimmt wird.

Siehe auch

• Prisma
• Pyramidenstumpf

Weblinks

Commons: Bipyramiden – Sammlung von Bildern, Videos und Audiodateien

• Eric W. Weisstein: Dipyramid. In: MathWorld (englisch).
• Bipyramiden auf mathematische-basteleien.de