5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number.
Humans, and many other animals, have 5 digits on their limbs.
Mathematics
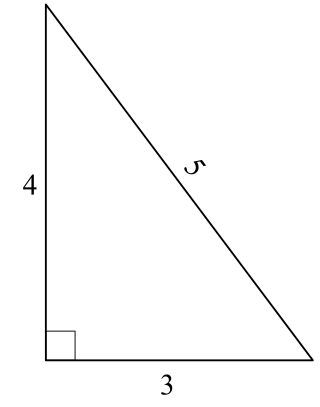
Five is the second Fermat prime, the third Mersenne prime exponent, as well as a Fibonacci number. 5 is the first congruent number, as well as the length of the hypotenuse of the smallest integer-sided right triangle, making part of the smallest Pythagorean triple (3, 4, 5).[1]
Geometry
A shape with five sides is called a pentagon. The pentagon is the first regular polygon that does not tile the plane with copies of itself. It is the largest face any of the five regular three-dimensional regular Platonic solid can have.
A conic is determined using five points in the same way that two points are needed to determine a line.[2]A pentagram, or five-pointed polygram, is a star polygon constructed by connecting some non-adjacent of a regular pentagon as self-intersecting edges.[3]
5 is the first safe prime[4], and the first good prime.[5] 11 forms the first pair of sexy primes with 5.[6] 5 is the second Fermat prime, of a total of five known Fermat primes.[7]
The internal geometry of the pentagon and pentagram (represented by its Schläfli symbol {5/2}) appears prominently in Penrose tilings. They are facets inside Kepler–Poinsot star polyhedra and Schläfli–Hess star polychora.
There are five Platonic solids in three-dimensional space that are regular: the tetrahedron, cube, octahedron, dodecahedron, and icosahedron.[8]
The chromatic number of the plane is the minimum number of colors required to color the plane such that no pair of points at a distance of 1 has the same color.[9] Five is a lower depending for the chromatic number of the plane, but this may depend on the choice of set-theoretical axioms:[10]
The plane contains a total of five Bravais lattices, or arrays of points defined by discrete translation operations. Uniform tilings of the plane, are generated from combinations of only five regular polygons.[11]
Higher Dimensional Geometry
A hypertetrahedron, or 5-cell the 4 dimensional analogue of the tetrahedron, has five vertices. Its orthographic projection is homomorphic to the group K5.[12]: p.120
There are five fundamental mirror symmetry point group families in 4-dimensions. There are also 5 compact hyperbolic Coxeter groups, or 4-prisms, of rank 5, each generating uniform honeycombs in hyperbolic 4-space as permutations of rings of the Coxeter diagrams.[13]

Algebra
5 is the value of the central cell of the first non-trivial normal magic square, called the Luoshu square. 5 is also the first of three known Wilson primes (5, 13, 563),[14] where the square of a prime divides As a consequence of Fermat's little theorem and Euler's criterion, all squares are congruent to 0, 1, 4 (or −1) modulo 5.[15] All integers can be expressed as the sum of five non-zero squares.[16][17] There are five countably infinite Ramsey classes of permutations.[18]: p.4
Five is conjectured to be the only odd, untouchable number; if this is the case, then five will be the only odd prime number that is not the base of an aliquot tree.[19]
Every odd number greater than five is conjectured to be expressible as the sum of three prime numbers; Helfgott has provided a proof of this[20] (also known as the odd Goldbach conjecture) that is already widely acknowledged by mathematicians as it still undergoes peer-review. On the other hand, every odd number greater than one is the sum of at most five prime numbers (as a lower limit).[21]


Group Theory
In graph theory, all graphs with four or fewer vertices are planar, however, there is a graph with five vertices that is not: K5, the complete graph with five vertices. By Kuratowski's theorem, a finite graph is planar if and only if it does not contain a subgraph that is a subdivision of , or K3,3, the utility graph.[22]
There are five complex exceptional Lie algebras. The five Mathieu groups constitute the first generation in the happy family of sporadic groups. These are also the first five sporadic groups to have been described.[23]: p.54 A centralizer of an element of order 5 inside the largest sporadic group arises from the product between Harada–Norton sporadic group and a group of order 5.[24][25]

 ).
). List of basic calculations
Evolution of the Arabic digit

The evolution of the modern Western digit for the numeral for five is traced back to the Indian system of numerals, where on some earlier versions, the numeral bore resemblance to variations of the number four, rather than "5" (as it is represented today). The Kushana and Gupta empires in what is now India had among themselves several forms that bear no resemblance to the modern digit. Later on, Arabic traditions transformed the digit in several ways, producing forms that were still similar to the numeral for four, with similarities to the numeral for three; yet, still unlike the modern five.[26] It was from those digits that Europeans finally came up with the modern 5 (represented in writings by Dürer, for example).
While the shape of the character for the digit 5 has an ascender in most modern typefaces, in typefaces with text figures the glyph usually has a descender, as, for example, in ![]() .
.

On the seven-segment display of a calculator and digital clock, it is represented by five segments at four successive turns from top to bottom, rotating counterclockwise first, then clockwise, and vice-versa. It is one of three numbers, along with 4 and 6, where the number of segments matches the number.
Other fields
Astronomy
There are five Lagrangian points in a two-body system.
Biology
There are usually considered to be five senses (in general terms); the five basic tastes are sweet, salty, sour, bitter, and umami.[27] Almost all amphibians, reptiles, and mammals which have fingers or toes have five of them on each extremity.[28] Five is the number of appendages on most starfish, which exhibit pentamerism.[29]
Computing
5 is the ASCII code of the Enquiry character, which is abbreviated to ENQ.[30]
Literature
Poetry
A pentameter is verse with five repeating feet per line; the iambic pentameter was the most prominent form used by William Shakespeare.[31]
Music
Modern musical notation uses a musical staff made of five horizontal lines.[32] A scale with five notes per octave is called a pentatonic scale.[33] A perfect fifth is the most consonant harmony, and is the basis for most western tuning systems.[34] In harmonics, the fifth partial (or 4th overtone) of a fundamental has a frequency ratio of 5:1 to the frequency of that fundamental. This ratio corresponds to the interval of 2 octaves plus a pure major third. Thus, the interval of 5:4 is the interval of the pure third. A major triad chord when played in just intonation (most often the case in a cappella vocal ensemble singing), will contain such a pure major third.
Five is the lowest possible number that can be the top number of a time signature with an asymmetric meter.
Religion
Judaism
The Book of Numbers is one of five books in the Torah; the others being the books of Genesis, Exodus, Leviticus, and Deuteronomy. They are collectively called the Five Books of Moses, the Pentateuch (Greek for "five containers", referring to the scroll cases in which the books were kept), or Humash (חומש, Hebrew for "fifth").[35] The Khamsa, an ancient symbol shaped like a hand with four fingers and one thumb, is used as a protective amulet by Jews; that same symbol is also very popular in Arabic culture, known to protect from envy and the evil eye.[36]
Christianity
There are traditionally five wounds of Jesus Christ in Christianity: the nail wounds in Christ's two hands, the nail wounds in Christ's two feet, and the Spear Wound of Christ (respectively at the four extremities of the body, and the head).[37]
Islam
The Five Pillars of Islam.[38] The five-pointed simple star ☆ is one of the five used in Islamic Girih tiles.[39]
Mysticism
Gnosticism
The number five was an important symbolic number in Manichaeism, with heavenly beings, concepts, and others often grouped in sets of five.
Alchemy
According to ancient Greek philosophers such as Aristotle, the universe is made up of five classical elements: water, earth, air, fire, and ether. This concept was later adopted by medieval alchemists and more recently by practitioners of Neo-Pagan religions such as Wicca. There are five elements in the universe according to Hindu cosmology: dharti, agni, jal, vayu evam akash (earth, fire, water, air and space, respectively). In East Asian tradition, there are five elements: water, fire, earth, wood, and metal.[40] The Japanese names for the days of the week, Tuesday through Saturday, come from these elements via the identification of the elements with the five planets visible with the naked eye.[41] Also, the traditional Japanese calendar has a five-day weekly cycle that can be still observed in printed mixed calendars combining Western, Chinese-Buddhist, and Japanese names for each weekday. There are also five elements in the traditional Chinese Wuxing.[42]
Quintessence, meaning "fifth element", refers to the elusive fifth element that completes the basic four elements (water, fire, air, and earth), as a union of these.[43] The pentagram, or five-pointed star, bears mystic significance in various belief systems including Baháʼí, Christianity, Freemasonry, Satanism, Taoism, Thelema, and Wicca.
Miscellaneous fields

- "Give me five" is a common phrase used preceding a high five.
- The Olympic Games have five interlocked rings as their symbol, representing the number of inhabited continents represented by the Olympians (Europe, Asia, Africa, Australia and Oceania, and the Americas).[44]
- The number of dots in a quincunx.[45]
See also
Notes
References
External links
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.




