Top Qs
Timeline
Chat
Perspective
Analytic geometry
Study of geometry using a coordinate system From Wikipedia, the free encyclopedia
Remove ads
Remove ads
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineering, and also in aviation, rocketry, space science, and spaceflight. It is the foundation of most modern fields of geometry, including algebraic, differential, discrete and computational geometry.
Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and circles, often in two and sometimes three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space. As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometric shapes in a numerical way and extracting numerical information from shapes' numerical definitions and representations. That the algebra of the real numbers can be employed to yield results about the linear continuum of geometry relies on the Cantor–Dedekind axiom.
Remove ads
History
Summarize
Perspective
Ancient Greece
The Greek mathematician Menaechmus solved problems and proved theorems by using a method that had a strong resemblance to the use of coordinates and it has sometimes been maintained that he had introduced analytic geometry.[1]
Apollonius of Perga, in On Determinate Section, dealt with problems in a manner that may be called an analytic geometry of one dimension; with the question of finding points on a line that were in a ratio to the others.[2] Apollonius in the Conics further developed a method that is so similar to analytic geometry that his work is sometimes thought to have anticipated the work of Descartes by some 1800 years. His application of reference lines, a diameter and a tangent is essentially no different from our modern use of a coordinate frame, where the distances measured along the diameter from the point of tangency are the abscissas, and the segments parallel to the tangent and intercepted between the axis and the curve are the ordinates. He further developed relations between the abscissas and the corresponding ordinates that are equivalent to rhetorical equations (expressed in words) of curves. However, although Apollonius came close to developing analytic geometry, he did not manage to do so since he did not take into account negative magnitudes and in every case the coordinate system was superimposed upon a given curve a posteriori instead of a priori. That is, equations were determined by curves, but curves were not determined by equations. Coordinates, variables, and equations were subsidiary notions applied to a specific geometric situation.[3]
Persia
The 11th-century Persian mathematician Omar Khayyam saw a strong relationship between geometry and algebra and was moving in the right direction when he helped close the gap between numerical and geometric algebra[4] with his geometric solution of the general cubic equations,[5] but the decisive step came later with Descartes.[4] Omar Khayyam is credited with identifying the foundations of algebraic geometry, and his book Treatise on Demonstrations of Problems of Algebra (1070), which laid down the principles of analytic geometry, is part of the body of Persian mathematics that was eventually transmitted to Europe.[6] Because of his thoroughgoing geometrical approach to algebraic equations, Khayyam can be considered a precursor to Descartes in the invention of analytic geometry.[7]: 248
Western Europe
Analytic geometry was independently invented by René Descartes and Pierre de Fermat,[8][9] although Descartes is sometimes given sole credit.[10][11] Cartesian geometry, the alternative term used for analytic geometry, is named after Descartes.
Descartes made significant progress with the methods in an essay titled La Géométrie (Geometry), one of the three accompanying essays (appendices) published in 1637 together with his Discourse on the Method for Rightly Directing One's Reason and Searching for Truth in the Sciences, commonly referred to as Discourse on Method. La Geometrie, written in his native French tongue, and its philosophical principles, provided a foundation for calculus in Europe. Initially the work was not well received, due, in part, to the many gaps in arguments and complicated equations. Only after the translation into Latin and the addition of commentary by van Schooten in 1649 (and further work thereafter) did Descartes's masterpiece receive due recognition.[12]
Pierre de Fermat also pioneered the development of analytic geometry. Although not published in his lifetime, a manuscript form of Ad locos planos et solidos isagoge (Introduction to Plane and Solid Loci) was circulating in Paris in 1637, just prior to the publication of Descartes' Discourse.[13][14][15] Clearly written and well received, the Introduction also laid the groundwork for analytical geometry. The key difference between Fermat's and Descartes' treatments is a matter of viewpoint: Fermat always started with an algebraic equation and then described the geometric curve that satisfied it, whereas Descartes started with geometric curves and produced their equations as one of several properties of the curves.[12] As a consequence of this approach, Descartes had to deal with more complicated equations and he had to develop the methods to work with polynomial equations of higher degree. It was Leonhard Euler who first applied the coordinate method in a systematic study of space curves and surfaces.
Remove ads
Coordinates
Summarize
Perspective

In analytic geometry, the plane is given a coordinate system, by which every point has a pair of real number coordinates. Similarly, Euclidean space is given coordinates where every point has three coordinates. The value of the coordinates depends on the choice of the initial point of origin. There are a variety of coordinate systems used, but the most common are the following:[16]
Cartesian coordinates (in a plane or space)
The most common coordinate system to use is the Cartesian coordinate system, where each point has an x-coordinate representing its horizontal position, and a y-coordinate representing its vertical position. These are typically written as an ordered pair (x, y). This system can also be used for three-dimensional geometry, where every point in Euclidean space is represented by an ordered triple of coordinates (x, y, z).
Polar coordinates (in a plane)
In polar coordinates, every point of the plane is represented by its distance r from the origin and its angle θ, with θ normally measured counterclockwise from the positive x-axis. Using this notation, points are typically written as an ordered pair (r, θ). One may transform back and forth between two-dimensional Cartesian and polar coordinates by using these formulae: This system may be generalized to three-dimensional space through the use of cylindrical or spherical coordinates.
Cylindrical coordinates (in a space)
In cylindrical coordinates, every point of space is represented by its height z, its radius r from the z-axis and the angle θ its projection on the xy-plane makes with respect to the horizontal axis.
Spherical coordinates (in a space)
In spherical coordinates, every point in space is represented by its distance ρ from the origin, the angle θ its projection on the xy-plane makes with respect to the horizontal axis, and the angle φ that it makes with respect to the z-axis. The names of the angles are often reversed in physics.[16]
Remove ads
Equations and curves
Summarize
Perspective
In analytic geometry, any equation involving the coordinates specifies a subset of the plane, namely the solution set for the equation, or locus. For example, the equation y = x corresponds to the set of all the points on the plane whose x-coordinate and y-coordinate are equal. These points form a line, and y = x is said to be the equation for this line. In general, linear equations involving x and y specify lines, quadratic equations specify conic sections, and more complicated equations describe more complicated figures.[17]
Usually, a single equation corresponds to a curve on the plane. This is not always the case: the trivial equation x = x specifies the entire plane, and the equation x2 + y2 = 0 specifies only the single point (0, 0). In three dimensions, a single equation usually gives a surface, and a curve must be specified as the intersection of two surfaces (see below), or as a system of parametric equations.[18] The equation x2 + y2 = r2 is the equation for any circle centered at the origin (0, 0) with a radius of r.
Lines and planes
Lines in a Cartesian plane, or more generally, in affine coordinates, can be described algebraically by linear equations. In two dimensions, the equation for non-vertical lines is often given in the slope-intercept form: where:
- m is the slope or gradient of the line.
- b is the y-intercept of the line.
- x is the independent variable of the function y = f(x).
In a manner analogous to the way lines in a two-dimensional space are described using a point-slope form for their equations, planes in a three dimensional space have a natural description using a point in the plane and a vector orthogonal to it (the normal vector) to indicate its "inclination".
Specifically, let be the position vector of some point , and let be a nonzero vector. The plane determined by this point and vector consists of those points , with position vector , such that the vector drawn from to is perpendicular to . Recalling that two vectors are perpendicular if and only if their dot product is zero, it follows that the desired plane can be described as the set of all points such that (The dot here means a dot product, not scalar multiplication.) Expanded this becomes which is the point-normal form of the equation of a plane.[citation needed] This is just a linear equation: Conversely, it is easily shown that if a, b, c and d are constants and a, b, and c are not all zero, then the graph of the equation is a plane having the vector as a normal.[citation needed] This familiar equation for a plane is called the general form of the equation of the plane.[19]
In three dimensions, lines can not be described by a single linear equation, so they are frequently described by parametric equations: where:
- x, y, and z are all functions of the independent variable t which ranges over the real numbers.
- (x0, y0, z0) is any point on the line.
- a, b, and c are related to the slope of the line, such that the vector (a, b, c) is parallel to the line.
Conic sections

In the Cartesian coordinate system, the graph of a quadratic equation in two variables is always a conic section – though it may be degenerate, and all conic sections arise in this way. The equation will be of the form As scaling all six constants yields the same locus of zeros, one can consider conics as points in the five-dimensional projective space
The conic sections described by this equation can be classified using the discriminant[20]
If the conic is non-degenerate, then:
- if , the equation represents an ellipse;
- if and , the equation represents a circle, which is a special case of an ellipse;
- if , the equation represents a parabola;
- if , the equation represents a hyperbola;
- if we also have , the equation represents a rectangular hyperbola.
Quadric surfaces
A quadric, or quadric surface, is a 2-dimensional surface in 3-dimensional space defined as the locus of zeros of a quadratic polynomial. In coordinates x1, x2,x3, the general quadric is defined by the algebraic equation[21]
Quadric surfaces include ellipsoids (including the sphere), paraboloids, hyperboloids, cylinders, cones, and planes.
Remove ads
Distance and angle
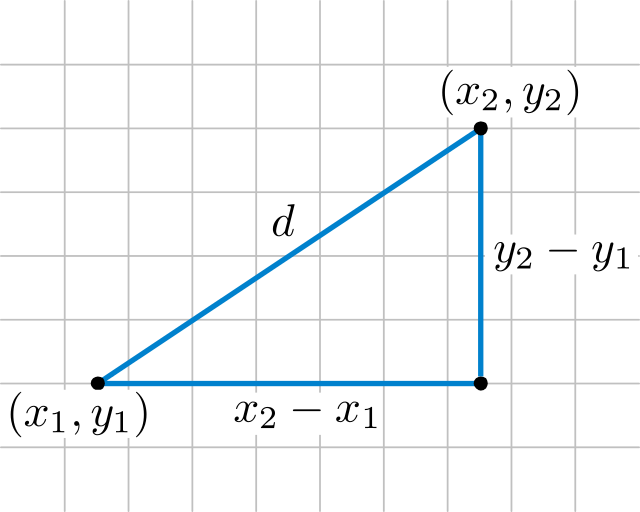
In analytic geometry, geometric notions such as distance and angle measure are defined using formulas. These definitions are designed to be consistent with the underlying Euclidean geometry. For example, using Cartesian coordinates on the plane, the distance between two points (x1, y1) and (x2, y2) is defined by the formula which can be viewed as a version of the Pythagorean theorem. Similarly, the angle that a line makes with the horizontal can be defined by the formula where m is the slope of the line.
In three dimensions, distance is given by the generalization of the Pythagorean theorem: while the angle between two vectors is given by the dot product. The dot product of two Euclidean vectors A and B is defined by[22] where θ is the angle between A and B.
Remove ads
Transformations
Summarize
Perspective

a) y = f(x) = |x| b) y = f(x+3) c) y = f(x)-3 d) y = 1/2 f(x)
Transformations are applied to a parent function to turn it into a new function with similar characteristics.
The graph of is changed by standard transformations as follows:
- Changing to moves the graph to the right units.
- Changing to moves the graph up units.
- Changing to stretches the graph horizontally by a factor of . (think of the as being dilated)
- Changing to stretches the graph vertically.
- Changing to and changing to rotates the graph by an angle .
There are other standard transformation not typically studied in elementary analytic geometry because the transformations change the shape of objects in ways not usually considered. Skewing is an example of a transformation not usually considered. For more information, consult the Wikipedia article on affine transformations.
For example, the parent function has a horizontal and a vertical asymptote, and occupies the first and third quadrant, and all of its transformed forms have one horizontal and vertical asymptote, and occupies either the 1st and 3rd or 2nd and 4th quadrant. In general, if , then it can be transformed into . In the new transformed function, is the factor that vertically stretches the function if it is greater than 1 or vertically compresses the function if it is less than 1, and for negative values, the function is reflected in the -axis. The value compresses the graph of the function horizontally if greater than 1 and stretches the function horizontally if less than 1, and like , reflects the function in the -axis when it is negative. The and values introduce translations, , vertical, and horizontal. Positive and values mean the function is translated to the positive end of its axis and negative meaning translation towards the negative end.
Transformations can be applied to any geometric equation whether or not the equation represents a function. Transformations can be considered as individual transactions or in combinations.
Suppose that is a relation in the plane. For example, is the relation that describes the unit circle.
Remove ads
Finding intersections of geometric objects
Summarize
Perspective
For two geometric objects P and Q represented by the relations and the intersection is the collection of all points which are in both relations.[23]
For example, might be the circle with radius 1 and center : and might be the circle with radius 1 and center . The intersection of these two circles is the collection of points which make both equations true. Does the point make both equations true? Using for , the equation for becomes or which is true, so is in the relation . On the other hand, still using for the equation for becomes or which is false. is not in so it is not in the intersection.
The intersection of and can be found by solving the simultaneous equations:
Traditional methods for finding intersections include substitution and elimination.
Substitution: Solve the first equation for in terms of and then substitute the expression for into the second equation:
We then substitute this value for into the other equation and proceed to solve for :
Next, we place this value of in either of the original equations and solve for :
So our intersection has two points:
Elimination: Add (or subtract) a multiple of one equation to the other equation so that one of the variables is eliminated. For our current example, if we subtract the first equation from the second we get . The in the first equation is subtracted from the in the second equation leaving no term. The variable has been eliminated. We then solve the remaining equation for , in the same way as in the substitution method:
We then place this value of in either of the original equations and solve for :
So our intersection has two points:
For conic sections, as many as 4 points might be in the intersection.
Finding intercepts
One type of intersection which is widely studied is the intersection of a geometric object with the and coordinate axes.
The intersection of a geometric object and the -axis is called the -intercept of the object. The intersection of a geometric object and the -axis is called the -intercept of the object.
For the line , the parameter specifies the point where the line crosses the axis. Depending on the context, either or the point is called the -intercept.
Remove ads
Geometric axis
Axis in geometry is the perpendicular line to any line, object or a surface.
Also for this may be used the common language use as a: normal (perpendicular) line, otherwise in engineering as axial line.
In geometry, a normal is an object such as a line or vector that is perpendicular to a given object. For example, in the two-dimensional case, the normal line to a curve at a given point is the line perpendicular to the tangent line to the curve at the point.
In the three-dimensional case a surface normal, or simply normal, to a surface at a point P is a vector that is perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a plane, the normal component of a force, the normal vector, etc. The concept of normality generalizes to orthogonality.
Remove ads
Spherical and nonlinear planes and their tangents
Tangent is the linear approximation of a spherical or other curved or twisted line of a function.
Tangent lines and planes
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Informally, it is a line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c on the curve if the line passes through the point (c, f(c)) on the curve and has slope f'(c) where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.
As it passes through the point where the tangent line and the curve meet, called the point of tangency, the tangent line is "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point.
Similarly, the tangent plane to a surface at a given point is the plane that "just touches" the surface at that point. The concept of a tangent is one of the most fundamental notions in differential geometry and has been extensively generalized; see Tangent space.
Remove ads
See also
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads










































































