Top Qs
Timeline
Chat
Perspective
Convex set
In geometry, set whose intersection with every line is a single line segment From Wikipedia, the free encyclopedia
Remove ads
In geometry, a set of points is convex if it contains every line segment between two points in the set.[1][2] For example, a solid cube is a convex set, but anything that is hollow or has an indent, such as a crescent shape, is not convex.
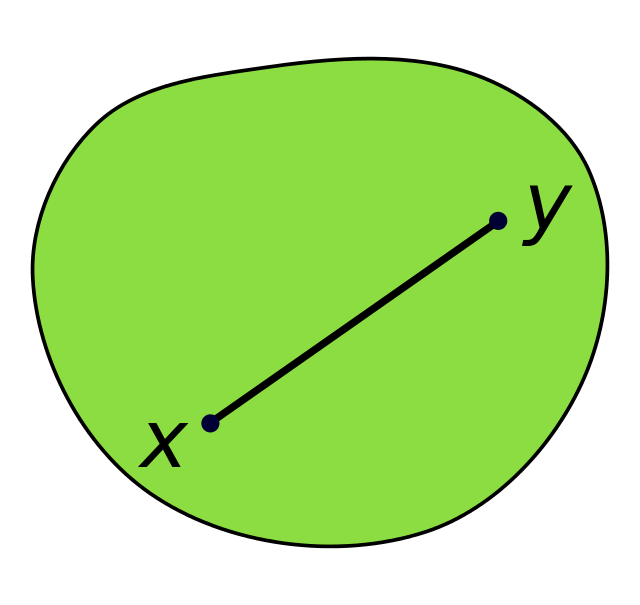

The boundary of a convex set in the plane is always a convex curve. The intersection of all the convex sets that contain a given subset A of Euclidean space is called the convex hull of A. It is the smallest convex set containing A.
A convex function is a real-valued function defined on an interval with the property that its epigraph (the set of points on or above the graph of the function) is a convex set. Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex sets. The branch of mathematics devoted to the study of properties of convex sets and convex functions is called convex analysis.
Spaces in which convex sets are defined include the Euclidean spaces, the affine spaces over the real numbers, and certain non-Euclidean geometries.
Remove ads
Definitions
Summarize
Perspective

Let S be a vector space or an affine space over the real numbers, or, more generally, over some ordered field (this includes Euclidean spaces, which are affine spaces). A subset C of S is convex if, for all x and y in C, the line segment connecting x and y is included in C.
This means that the affine combination (1 − t)x + ty belongs to C for all x,y in C and t in the interval [0, 1]. This implies that convexity is invariant under affine transformations. Further, it implies that a convex set in a real or complex topological vector space is path-connected (and therefore also connected).
A set C is strictly convex if every point on the line segment connecting x and y other than the endpoints is inside the topological interior of C. A closed convex subset is strictly convex if and only if every one of its boundary points is an extreme point.[3]
A set C is absolutely convex if it is convex and balanced.
Examples
The convex subsets of R (the set of real numbers) are the intervals and the points of R. Some examples of convex subsets of the Euclidean plane are solid regular polygons, solid triangles, and intersections of solid triangles. Some examples of convex subsets of a Euclidean 3-dimensional space are the Archimedean solids and the Platonic solids. The Kepler-Poinsot polyhedra are examples of non-convex sets.
Non-convex set
A set that is not convex is called a non-convex set. A polygon that is not a convex polygon is sometimes called a concave polygon,[4] and some sources more generally use the term concave set to mean a non-convex set,[5] but most authorities prohibit this usage.[6][7]
The complement of a convex set, such as the epigraph of a concave function, is sometimes called a reverse convex set, especially in the context of mathematical optimization.[8]
Remove ads
Properties
Summarize
Perspective
Given r points u1, ..., ur in a convex set S, and r nonnegative numbers λ1, ..., λr such that λ1 + ... + λr = 1, the affine combination belongs to S. As the definition of a convex set is the case r = 2, this property characterizes convex sets.
Such an affine combination is called a convex combination of u1, ..., ur. The convex hull of a subset S of a real vector space is defined as the intersection of all convex sets that contain S. More concretely, the convex hull is the set of all convex combinations of points in S. In particular, this is a convex set.
A (bounded) convex polytope is the convex hull of a finite subset of some Euclidean space Rn.
Intersections and unions
The collection of convex subsets of a vector space, an affine space, or a Euclidean space has the following properties:[9][10]
- The empty set and the whole space are convex.
- The intersection of any collection of convex sets is convex.
- The union of a collection of convex sets is convex if those sets form a chain (a totally ordered set) under inclusion. For this property, the restriction to chains is important, as the union of two convex sets need not be convex.
Closed convex sets
Closed convex sets are convex sets that contain all their limit points. They can be characterised as the intersections of closed half-spaces (sets of points in space that lie on and to one side of a hyperplane).
From what has just been said, it is clear that such intersections are convex, and they will also be closed sets. To prove the converse, i.e., every closed convex set may be represented as such intersection, one needs the supporting hyperplane theorem in the form that for a given closed convex set C and point P outside it, there is a closed half-space H that contains C and not P. The supporting hyperplane theorem is a special case of the Hahn–Banach theorem of functional analysis.
Face of a convex set
A face of a convex set is a convex subset of such that whenever a point in lies strictly between two points and in , both and must be in .[11] Equivalently, for any and any real number such that is in , and must be in . According to this definition, itself and the empty set are faces of ; these are sometimes called the trivial faces of . An extreme point of is a point that is a face of .
Let be a convex set in that is compact (or equivalently, closed and bounded). Then is the convex hull of its extreme points.[12] More generally, each compact convex set in a locally convex topological vector space is the closed convex hull of its extreme points (the Krein–Milman theorem).
For example:
- A triangle in the plane (including the region inside) is a compact convex set. Its nontrivial faces are the three vertices and the three edges. (So the only extreme points are the three vertices.)
- The only nontrivial faces of the closed unit disk are its extreme points, namely the points on the unit circle .
Convex sets and rectangles
Let C be a convex body in the plane (a convex set whose interior is non-empty). We can inscribe a rectangle r in C such that a homothetic copy R of r is circumscribed about C. The positive homothety ratio is at most 2 and:[13]
Blaschke-Santaló diagrams
The set of all planar convex bodies can be parameterized in terms of the convex body diameter D, its inradius r (the biggest circle contained in the convex body) and its circumradius R (the smallest circle containing the convex body). In fact, this set can be described by the set of inequalities given by[14][15] and can be visualized as the image of the function g that maps a convex body to the R2 point given by (r/R, D/2R). The image of this function is known a (r, D, R) Blachke-Santaló diagram.[15]

Alternatively, the set can also be parametrized by its width (the smallest distance between any two different parallel support hyperplanes), perimeter and area.[14][15]
Other properties
Let X be a topological vector space and be convex.
- and are both convex (i.e. the closure and interior of convex sets are convex).
- If and then (where ).
- If then:
- , and
- , where is the algebraic interior of C.
Remove ads
Convex hulls and Minkowski sums
Summarize
Perspective
Convex hulls
Every subset A of the vector space is contained within a smallest convex set (called the convex hull of A), namely the intersection of all convex sets containing A. The convex-hull operator Conv() has the characteristic properties of a closure operator:
- extensive: S ⊆ Conv(S),
- non-decreasing: S ⊆ T implies that Conv(S) ⊆ Conv(T), and
- idempotent: Conv(Conv(S)) = Conv(S).
The convex-hull operation is needed for the set of convex sets to form a lattice, in which the "join" operation is the convex hull of the union of two convex sets The intersection of any collection of convex sets is itself convex, so the convex subsets of a (real or complex) vector space form a complete lattice.
Minkowski addition

In a real vector-space, the Minkowski sum of two (non-empty) sets, S1 and S2, is defined to be the set S1 + S2 formed by the addition of vectors element-wise from the summand-sets More generally, the Minkowski sum of a finite family of (non-empty) sets Sn is the set formed by element-wise addition of vectors
For Minkowski addition, the zero set {0} containing only the zero vector 0 has special importance: For every non-empty subset S of a vector space in algebraic terminology, {0} is the identity element of Minkowski addition (on the collection of non-empty sets).[16]
Convex hulls of Minkowski sums
Minkowski addition behaves well with respect to the operation of taking convex hulls, as shown by the following proposition:
Let S1, S2 be subsets of a real vector-space, the convex hull of their Minkowski sum is the Minkowski sum of their convex hulls
This result holds more generally for each finite collection of non-empty sets:
In mathematical terminology, the operations of Minkowski summation and of forming convex hulls are commuting operations.[17][18]
Minkowski sums of convex sets
The Minkowski sum of two compact convex sets is compact. The sum of a compact convex set and a closed convex set is closed.[19]
The following famous theorem, proved by Dieudonné in 1966, gives a sufficient condition for the difference of two closed convex subsets to be closed.[20] It uses the concept of a recession cone of a non-empty convex subset S, defined as: where this set is a convex cone containing and satisfying . Note that if S is closed and convex then is closed and for all ,
Theorem (Dieudonné). Let A and B be non-empty, closed, and convex subsets of a locally convex topological vector space such that is a linear subspace. If A or B is locally compact then A − B is closed.
Remove ads
Generalizations and extensions for convexity
Summarize
Perspective
The notion of convexity in the Euclidean space may be generalized by modifying the definition in some or other aspects. The common name "generalized convexity" is used, because the resulting objects retain certain properties of convex sets.
Star-convex (star-shaped) sets
Let C be a set in a real or complex vector space. C is star convex (star-shaped) if there exists an x0 in C such that the line segment from x0 to any point y in C is contained in C. Hence a non-empty convex set is always star-convex but a star-convex set is not always convex.
Orthogonal convexity
An example of generalized convexity is orthogonal convexity.[21]
A set S in the Euclidean space is called orthogonally convex or ortho-convex, if any segment parallel to any of the coordinate axes connecting two points of S lies totally within S. It is easy to prove that an intersection of any collection of orthoconvex sets is orthoconvex. Some other properties of convex sets are valid as well.
Non-Euclidean geometry
The definition of a convex set and a convex hull extends naturally to geometries which are not Euclidean by defining a geodesically convex set to be one that contains the geodesics joining any two points in the set.
Order topology
Convexity can be extended for a totally ordered set X endowed with the order topology.[22]
Let Y ⊆ X. The subspace Y is a convex set if for each pair of points a, b in Y such that a ≤ b, the interval [a, b] = {x ∈ X | a ≤ x ≤ b} is contained in Y. That is, Y is convex if and only if for all a, b in Y, a ≤ b implies [a, b] ⊆ Y.
A convex set is not connected in general: a counter-example is given by the subspace {1,2,3} in Z, which is both convex and not connected.
Convexity spaces
The notion of convexity may be generalised to other objects, if certain properties of convexity are selected as axioms.
Given a set X, a convexity over X is a collection 𝒞 of subsets of X satisfying the following axioms:[9][10][23]
- The empty set and X are in 𝒞.
- The intersection of any collection from 𝒞 is in 𝒞.
- The union of a chain (with respect to the inclusion relation) of elements of 𝒞 is in 𝒞.
The elements of 𝒞 are called convex sets and the pair (X, 𝒞) is called a convexity space. For the ordinary convexity, the first two axioms hold, and the third one is trivial.
For an alternative definition of abstract convexity, more suited to discrete geometry, see the convex geometries associated with antimatroids.
Convex spaces
Convexity can be generalised as an abstract algebraic structure: a space is convex if it is possible to take convex combinations of points.
Remove ads
See also
- Absorbing set
- Algorithmic problems on convex sets
- Bounded set (topological vector space)
- Brouwer fixed-point theorem
- Complex convexity
- Convex cone
- Convex series
- Convex metric space
- Carathéodory's theorem (convex hull)
- Choquet theory
- Helly's theorem
- Holomorphically convex hull
- Integrally-convex set
- John ellipsoid
- Pseudoconvexity
- Radon's theorem
- Shapley–Folkman lemma
- Symmetric set
References
Bibliography
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads














































