Top Qs
Timeline
Chat
Perspective
Dimension
Property of a mathematical space From Wikipedia, the free encyclopedia
Remove ads
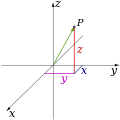
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it.[1][2] Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on it – for example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on it – for example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces.

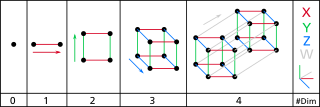
- Two points can be connected to create a line segment.
- Two parallel line segments can be connected to form a square.
- Two parallel squares can be connected to form a cube.
- Two parallel cubes can be connected to form a tesseract.
In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that was found necessary to describe electromagnetism. The four dimensions (4D) of spacetime consist of events that are not absolutely defined spatially and temporally, but rather are known relative to the motion of an observer. Minkowski space first approximates the universe without gravity; the pseudo-Riemannian manifolds of general relativity describe spacetime with matter and gravity. 10 dimensions are used to describe superstring theory (6D hyperspace + 4D), 11 dimensions can describe supergravity and M-theory (7D hyperspace + 4D), and the state-space of quantum mechanics is an infinite-dimensional function space.
The concept of dimension is not restricted to physical objects. High-dimensional spaces frequently occur in mathematics and the sciences. They may be Euclidean spaces or more general parameter spaces or configuration spaces such as in Lagrangian or Hamiltonian mechanics; these are abstract spaces, independent of the physical space.
Remove ads
In mathematics
Summarize
Perspective
In mathematics, the dimension of an object is, roughly speaking, the number of degrees of freedom of a point that moves on this object. In other words, the dimension is the number of independent parameters or coordinates that are needed for defining the position of a point that is constrained to be on the object. For example, the dimension of a point is zero; the dimension of a line is one, as a point can move on a line in only one direction (or its opposite); the dimension of a plane is two, etc.
The dimension is an intrinsic property of an object, in the sense that it is independent of the dimension of the space in which the object is or can be embedded. For example, a curve, such as a circle, is of dimension one, because the position of a point on a curve is determined by its signed distance along the curve to a fixed point on the curve. This is independent from the fact that a curve cannot be embedded in a Euclidean space of dimension lower than two, unless it is a line. Similarly, a surface is of dimension two, even if embedded in three-dimensional space.
The dimension of Euclidean n-space En is n. When trying to generalize to other types of spaces, one is faced with the question "what makes En n-dimensional?" One answer is that to cover a fixed ball in En by small balls of radius ε, one needs on the order of ε−n such small balls. This observation leads to the definition of the Minkowski dimension and its more sophisticated variant, the Hausdorff dimension, but there are also other answers to that question. For example, the boundary of a ball in En looks locally like En-1 and this leads to the notion of the inductive dimension. While these notions agree on En, they turn out to be different when one looks at more general spaces.
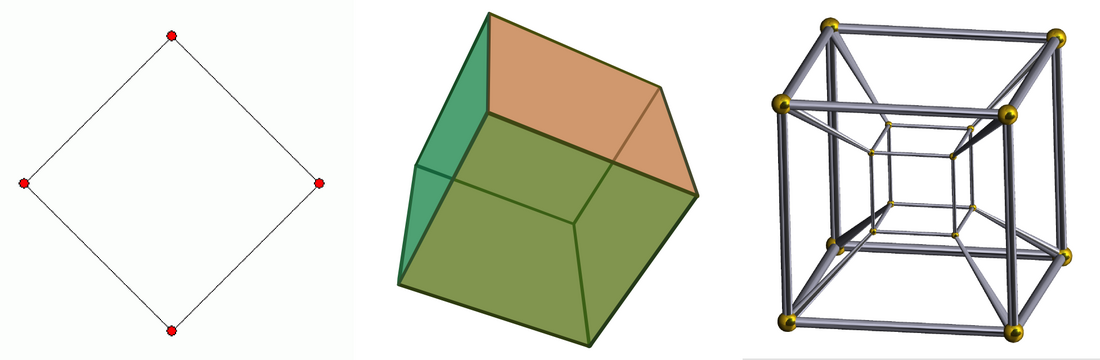
A tesseract is an example of a four-dimensional object. Whereas outside mathematics the use of the term "dimension" is as in: "A tesseract has four dimensions", mathematicians usually express this as: "The tesseract has dimension 4", or: "The dimension of the tesseract is 4".
Although the notion of higher dimensions goes back to René Descartes, substantial development of a higher-dimensional geometry only began in the 19th century, via the work of Arthur Cayley, William Rowan Hamilton, Ludwig Schläfli and Bernhard Riemann. Riemann's 1854 Habilitationsschrift, Schläfli's 1852 Theorie der vielfachen Kontinuität, and Hamilton's discovery of the quaternions and John T. Graves' discovery of the octonions in 1843 marked the beginning of higher-dimensional geometry.
The rest of this section examines some of the more important mathematical definitions of dimension.
Vector spaces
The dimension of a vector space is the number of vectors in any basis for the space, i.e. the number of coordinates necessary to specify any vector. This notion of dimension (the cardinality of a basis) is often referred to as the Hamel dimension or algebraic dimension to distinguish it from other notions of dimension.
For the non-free case, this generalizes to the notion of the length of a module.
Manifolds
The uniquely defined dimension of every connected topological manifold can be calculated. A connected topological manifold is locally homeomorphic to Euclidean n-space, in which the number n is the manifold's dimension.
For connected differentiable manifolds, the dimension is also the dimension of the tangent vector space at any point.
In geometric topology, the theory of manifolds is characterized by the way dimensions 1 and 2 are relatively elementary, the high-dimensional cases n > 4 are simplified by having extra space in which to "work"; and the cases n = 3 and 4 are in some senses the most difficult. This state of affairs was highly marked in the various cases of the Poincaré conjecture, in which four different proof methods are applied.
Complex dimension

The dimension of a manifold depends on the base field with respect to which Euclidean space is defined. While analysis usually assumes a manifold to be over the real numbers, it is sometimes useful in the study of complex manifolds and algebraic varieties to work over the complex numbers instead. A complex number (x + iy) has a real part x and an imaginary part y, in which x and y are both real numbers; hence, the complex dimension is half the real dimension.
Conversely, in algebraically unconstrained contexts, a single complex coordinate system may be applied to an object having two real dimensions. For example, an ordinary two-dimensional spherical surface, when given a complex metric, becomes a Riemann sphere of one complex dimension.[3]
Varieties
The dimension of an algebraic variety may be defined in various equivalent ways. The most intuitive way is probably the dimension of the tangent space at any Regular point of an algebraic variety. Another intuitive way is to define the dimension as the number of hyperplanes that are needed in order to have an intersection with the variety that is reduced to a finite number of points (dimension zero). This definition is based on the fact that the intersection of a variety with a hyperplane reduces the dimension by one unless if the hyperplane contains the variety.
An algebraic set being a finite union of algebraic varieties, its dimension is the maximum of the dimensions of its components. It is equal to the maximal length of the chains of sub-varieties of the given algebraic set (the length of such a chain is the number of "").
Each variety can be considered as an algebraic stack, and its dimension as variety agrees with its dimension as stack. There are however many stacks which do not correspond to varieties, and some of these have negative dimension. Specifically, if V is a variety of dimension m and G is an algebraic group of dimension n acting on V, then the quotient stack [V/G] has dimension m − n.[4]
Krull dimension
The Krull dimension of a commutative ring is the maximal length of chains of prime ideals in it, a chain of length n being a sequence of prime ideals related by inclusion. It is strongly related to the dimension of an algebraic variety, because of the natural correspondence between sub-varieties and prime ideals of the ring of the polynomials on the variety.
For an algebra over a field, the dimension as vector space is finite if and only if its Krull dimension is 0.
Topological spaces
For any normal topological space X, the Lebesgue covering dimension of X is defined to be the smallest integer n for which the following holds: any open cover has an open refinement (a second open cover in which each element is a subset of an element in the first cover) such that no point is included in more than n + 1 elements. In this case dim X = n. For X a manifold, this coincides with the dimension mentioned above. If no such integer n exists, then the dimension of X is said to be infinite, and one writes dim X = ∞. Moreover, X has dimension −1, i.e. dim X = −1 if and only if X is empty. This definition of covering dimension can be extended from the class of normal spaces to all Tychonoff spaces merely by replacing the term "open" in the definition by the term "functionally open".
An inductive dimension may be defined inductively as follows. Consider a discrete set of points (such as a finite collection of points) to be 0-dimensional. By dragging a 0-dimensional object in some direction, one obtains a 1-dimensional object. By dragging a 1-dimensional object in a new direction, one obtains a 2-dimensional object. In general, one obtains an (n + 1)-dimensional object by dragging an n-dimensional object in a new direction. The inductive dimension of a topological space may refer to the small inductive dimension or the large inductive dimension, and is based on the analogy that, in the case of metric spaces, (n + 1)-dimensional balls have n-dimensional boundaries, permitting an inductive definition based on the dimension of the boundaries of open sets. Moreover, the boundary of a discrete set of points is the empty set, and therefore the empty set can be taken to have dimension −1.[5]
Similarly, for the class of CW complexes, the dimension of an object is the largest n for which the n-skeleton is nontrivial. Intuitively, this can be described as follows: if the original space can be continuously deformed into a collection of higher-dimensional triangles joined at their faces with a complicated surface, then the dimension of the object is the dimension of those triangles.[citation needed]
Hausdorff dimension
The Hausdorff dimension is useful for studying structurally complicated sets, especially fractals. The Hausdorff dimension is defined for all metric spaces and, unlike the dimensions considered above, can also have non-integer real values.[6] The box dimension or Minkowski dimension is a variant of the same idea. In general, there exist more definitions of fractal dimensions that work for highly irregular sets and attain non-integer positive real values.
Hilbert spaces
Every Hilbert space admits an orthonormal basis, and any two such bases for a particular space have the same cardinality. This cardinality is called the dimension of the Hilbert space. This dimension is finite if and only if the space's Hamel dimension is finite, and in this case the two dimensions coincide.
Remove ads
In physics
Summarize
Perspective
Spatial dimensions
Classical physics theories describe three physical dimensions: from a particular point in space, the basic directions in which we can move are up/down, left/right, and forward/backward. Movement in any other direction can be expressed in terms of just these three. Moving down is the same as moving up a negative distance. Moving diagonally upward and forward is just as the name of the direction implies i.e., moving in a linear combination of up and forward. In its simplest form: a line describes one dimension, a plane describes two dimensions, and a cube describes three dimensions. (See Space and Cartesian coordinate system.)
Time
A temporal dimension, or time dimension, is a dimension of time. Time is often referred to as the "fourth dimension" for this reason, but that is not to imply that it is a spatial dimension.[7] A temporal dimension is one way to measure physical change. It is perceived differently from the three spatial dimensions in that there is only one of it, and that we cannot move freely in time but subjectively move in one direction.
The equations used in physics to model reality do not treat time in the same way that humans commonly perceive it. The equations of classical mechanics are symmetric with respect to time, and equations of quantum mechanics are typically symmetric if both time and other quantities (such as charge and parity) are reversed. In these models, the perception of time flowing in one direction is an artifact of the laws of thermodynamics (we perceive time as flowing in the direction of increasing entropy).
The best-known treatment of time as a dimension is Poincaré and Einstein's special relativity (and extended to general relativity), which treats perceived space and time as components of a four-dimensional manifold, known as spacetime, and in the special, flat case as Minkowski space. Time is different from other spatial dimensions as time operates in all spatial dimensions. Time operates in the first, second and third as well as theoretical spatial dimensions such as a fourth spatial dimension. Time is not however present in a single point of absolute infinite singularity as defined as a geometric point, as an infinitely small point can have no change and therefore no time. Just as when an object moves through positions in space, it also moves through positions in time. In this sense the force moving any object to change is time.[8][9][10]
Additional dimensions
In physics, three dimensions of space and one of time is the accepted norm. However, there are theories that attempt to unify the four fundamental forces by introducing extra dimensions/hyperspace. Most notably, superstring theory requires 10 spacetime dimensions, and originates from a more fundamental 11-dimensional theory tentatively called M-theory which subsumes five previously distinct superstring theories. Supergravity theory also promotes 11D spacetime = 7D hyperspace + 4 common dimensions. To date, no direct experimental or observational evidence is available to support the existence of these extra dimensions. If hyperspace exists, it must be hidden from us by some physical mechanism. One well-studied possibility is that the extra dimensions may be "curled up" (compactified) at such tiny scales as to be effectively invisible to current experiments.

In 1921, Kaluza–Klein theory presented 5D including an extra dimension of space. At the level of quantum field theory, Kaluza–Klein theory unifies gravity with gauge interactions, based on the realization that gravity propagating in small, compact extra dimensions is equivalent to gauge interactions at long distances. In particular when the geometry of the extra dimensions is trivial, it reproduces electromagnetism. However, at sufficiently high energies or short distances, this setup still suffers from the same pathologies that famously obstruct direct attempts to describe quantum gravity. Therefore, these models still require a UV completion, of the kind that string theory is intended to provide. In particular, superstring theory requires six compact dimensions (6D hyperspace) forming a Calabi–Yau manifold. Thus Kaluza-Klein theory may be considered either as an incomplete description on its own, or as a subset of string theory model building.
In addition to small and curled up extra dimensions, there may be extra dimensions that instead are not apparent because the matter associated with our visible universe is localized on a (3 + 1)-dimensional subspace. Thus, the extra dimensions need not be small and compact but may be large extra dimensions. D-branes are dynamical extended objects of various dimensionalities predicted by string theory that could play this role. They have the property that open string excitations, which are associated with gauge interactions, are confined to the brane by their endpoints, whereas the closed strings that mediate the gravitational interaction are free to propagate into the whole spacetime, or "the bulk". This could be related to why gravity is exponentially weaker than the other forces, as it effectively dilutes itself as it propagates into a higher-dimensional volume.
Some aspects of brane physics have been applied to cosmology. For example, brane gas cosmology[11][12] attempts to explain why there are three dimensions of space using topological and thermodynamic considerations. According to this idea it would be since three is the largest number of spatial dimensions in which strings can generically intersect. If initially there are many windings of strings around compact dimensions, space could only expand to macroscopic sizes once these windings are eliminated, which requires oppositely wound strings to find each other and annihilate. But strings can only find each other to annihilate at a meaningful rate in three dimensions, so it follows that only three dimensions of space are allowed to grow large given this kind of initial configuration. Extra dimensions are said to be universal if all fields are equally free to propagate within them.
In 2024, Günther Kletetschka propounded that time exists in three dimensions, and that these three temporal dimensions naturally generate our three spatial dimensions, creating a six-dimensional universe with matter, energy, and their fundamental interactions. Kletetschka proposed his six-dimensional universe in a paper entitled Three-Dimensional Time: A Mathematical Framework for Fundamental Physics.[13] Kletetschka's mathematical framework maintains causality, accurately calculates fermion masses, and makes specific predictions for the discovery of quantum gravity.[14] Kletetschka proposed numerous experiments to test his mathematical framework.[13]
Remove ads
In computer graphics and spatial data
Summarize
Perspective
Several types of digital systems are based on the storage, analysis, and visualization of geometric shapes, including illustration software, computer-aided design, and geographic information systems. Different vector systems use a wide variety of data structures to represent shapes, but almost all are fundamentally based on a set of geometric primitives corresponding to the spatial dimensions:[15]
- Point (0-dimensional), a single coordinate in a Cartesian coordinate system.
- Line or Polyline (1-dimensional) usually represented as an ordered list of points sampled from a continuous line, whereupon the software is expected to interpolate the intervening shape of the line as straight- or curved-line segments.
- Polygon (2-dimensional) usually represented as a line that closes at its endpoints, representing the boundary of a two-dimensional region. The software is expected to use this boundary to partition 2-dimensional space into an interior and exterior.
- Surface (3-dimensional) represented using a variety of strategies, such as a polyhedron consisting of connected polygon faces. The software is expected to use this surface to partition 3-dimensional space into an interior and exterior.
Frequently in these systems, especially GIS and cartography, a representation of a real-world phenomenon may have a different (usually lower) dimension than the phenomenon being represented. For example, a city (a two-dimensional region) may be represented as a point, or a road (a three-dimensional volume of material) may be represented as a line. This dimensional generalization correlates with tendencies in spatial cognition. For example, asking the distance between two cities presumes a conceptual model of the cities as points, while giving directions involving travel "up," "down," or "along" a road imply a one-dimensional conceptual model. This is frequently done for purposes of data efficiency, visual simplicity, or cognitive efficiency, and is acceptable if the distinction between the representation and the represented is understood but can cause confusion if information users assume that the digital shape is a perfect representation of reality (i.e., believing that roads really are lines).
Remove ads
More dimensions
- Degrees of freedom
- in mechanics
- in physics and chemistry
- in statistics
- Exterior dimension
- Hurst exponent
- Isoperimetric dimension
- Metric dimension
- Order dimension
- q-dimension
List of topics by dimension
- 0 dimension
- 1 dimension
- 2 dimensions
- 3 dimensions
- 4 dimensions
- 5 dimensions
- 8 dimensions
- 10 dimensions
- 11 dimensions
- 12 dimensions
- 16 dimensions
- 26 dimensions
- 32 dimensions
- Higher dimensions
- Infinite
Remove ads
See also
References
Further reading
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads