Loading AI tools
Unbounded quadric surface From Wikipedia, the free encyclopedia
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.
 Hyperboloid of one sheet |
 conical surface in between |
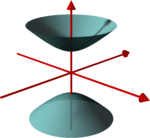 Hyperboloid of two sheets |
A hyperboloid is a quadric surface, that is, a surface defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry.
Given a hyperboloid, one can choose a Cartesian coordinate system such that the hyperboloid is defined by one of the following equations: or The coordinate axes are axes of symmetry of the hyperboloid and the origin is the center of symmetry of the hyperboloid. In any case, the hyperboloid is asymptotic to the cone of the equations:
One has a hyperboloid of revolution if and only if Otherwise, the axes are uniquely defined (up to the exchange of the x-axis and the y-axis).
There are two kinds of hyperboloids. In the first case (+1 in the right-hand side of the equation): a one-sheet hyperboloid, also called a hyperbolic hyperboloid. It is a connected surface, which has a negative Gaussian curvature at every point. This implies near every point the intersection of the hyperboloid and its tangent plane at the point consists of two branches of curve that have distinct tangents at the point. In the case of the one-sheet hyperboloid, these branches of curves are lines and thus the one-sheet hyperboloid is a doubly ruled surface.
In the second case (−1 in the right-hand side of the equation): a two-sheet hyperboloid, also called an elliptic hyperboloid. The surface has two connected components and a positive Gaussian curvature at every point. The surface is convex in the sense that the tangent plane at every point intersects the surface only in this point.

Cartesian coordinates for the hyperboloids can be defined, similar to spherical coordinates, keeping the azimuth angle θ ∈ [0, 2π), but changing inclination v into hyperbolic trigonometric functions:
One-surface hyperboloid: v ∈ (−∞, ∞)
Two-surface hyperboloid: v ∈ [0, ∞)


The following parametric representation includes hyperboloids of one sheet, two sheets, and their common boundary cone, each with the -axis as the axis of symmetry:
One can obtain a parametric representation of a hyperboloid with a different coordinate axis as the axis of symmetry by shuffling the position of the term to the appropriate component in the equation above.
More generally, an arbitrarily oriented hyperboloid, centered at v, is defined by the equation where A is a matrix and x, v are vectors.
The eigenvectors of A define the principal directions of the hyperboloid and the eigenvalues of A are the reciprocals of the squares of the semi-axes: , and . The one-sheet hyperboloid has two positive eigenvalues and one negative eigenvalue. The two-sheet hyperboloid has one positive eigenvalue and two negative eigenvalues.
If the hyperboloid has the equation then the lines
are contained in the surface.
In case the hyperboloid is a surface of revolution and can be generated by rotating one of the two lines or , which are skew to the rotation axis (see picture). This property is called Wren's theorem.[1] The more common generation of a one-sheet hyperboloid of revolution is rotating a hyperbola around its semi-minor axis (see picture; rotating the hyperbola around its other axis gives a two-sheet hyperbola of revolution).
A hyperboloid of one sheet is projectively equivalent to a hyperbolic paraboloid.
For simplicity the plane sections of the unit hyperboloid with equation are considered. Because a hyperboloid in general position is an affine image of the unit hyperboloid, the result applies to the general case, too.
Obviously, any one-sheet hyperboloid of revolution contains circles. This is also true, but less obvious, in the general case (see circular section).


The hyperboloid of two sheets does not contain lines. The discussion of plane sections can be performed for the unit hyperboloid of two sheets with equation which can be generated by a rotating hyperbola around one of its axes (the one that cuts the hyperbola)
Obviously, any two-sheet hyperboloid of revolution contains circles. This is also true, but less obvious, in the general case (see circular section).
Remark: A hyperboloid of two sheets is projectively equivalent to a sphere.
The hyperboloids with equations are
Whereas the Gaussian curvature of a hyperboloid of one sheet is negative, that of a two-sheet hyperboloid is positive. In spite of its positive curvature, the hyperboloid of two sheets with another suitably chosen metric can also be used as a model for hyperbolic geometry.
Imaginary hyperboloids are frequently found in mathematics of higher dimensions. For example, in a pseudo-Euclidean space one has the use of a quadratic form: When c is any constant, then the part of the space given by is called a hyperboloid. The degenerate case corresponds to c = 0.
As an example, consider the following passage:[4]
... the velocity vectors always lie on a surface which Minkowski calls a four-dimensional hyperboloid since, expressed in terms of purely real coordinates (y1, ..., y4), its equation is y2
1 + y2
2 + y2
3 − y2
4 = −1, analogous to the hyperboloid y2
1 + y2
2 − y2
3 = −1 of three-dimensional space.[6]
However, the term quasi-sphere is also used in this context since the sphere and hyperboloid have some commonality (See § Relation to the sphere below).
One-sheeted hyperboloids are used in construction, with the structures called hyperboloid structures. A hyperboloid is a doubly ruled surface; thus, it can be built with straight steel beams, producing a strong structure at a lower cost than other methods. Examples include cooling towers, especially of power stations, and many other structures.
In 1853 William Rowan Hamilton published his Lectures on Quaternions which included presentation of biquaternions. The following passage from page 673 shows how Hamilton uses biquaternion algebra and vectors from quaternions to produce hyperboloids from the equation of a sphere:
... the equation of the unit sphere ρ2 + 1 = 0, and change the vector ρ to a bivector form, such as σ + τ √−1. The equation of the sphere then breaks up into the system of the two following,
σ2 − τ2 + 1 = 0, S.στ = 0;and suggests our considering σ and τ as two real and rectangular vectors, such that
Tτ = (Tσ2 − 1 )1/2.Hence it is easy to infer that if we assume σ || λ, where λ is a vector in a given position, the new real vector σ + τ will terminate on the surface of a double-sheeted and equilateral hyperboloid; and that if, on the other hand, we assume τ || λ, then the locus of the extremity of the real vector σ + τ will be an equilateral but single-sheeted hyperboloid. The study of these two hyperboloids is, therefore, in this way connected very simply, through biquaternions, with the study of the sphere; ...
In this passage S is the operator giving the scalar part of a quaternion, and T is the "tensor", now called norm, of a quaternion.
A modern view of the unification of the sphere and hyperboloid uses the idea of a conic section as a slice of a quadratic form. Instead of a conical surface, one requires conical hypersurfaces in four-dimensional space with points p = (w, x, y, z) ∈ R4 determined by quadratic forms. First consider the conical hypersurface
Then is the sphere with radius r. On the other hand, the conical hypersurface
In the theory of quadratic forms, a unit quasi-sphere is the subset of a quadratic space X consisting of the x ∈ X such that the quadratic norm of x is one.[7]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.