Top Qs
Timeline
Chat
Perspective
Hypergraph
Generalization of graph theory From Wikipedia, the free encyclopedia
Remove ads
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices.


Formally, a directed hypergraph is a pair , where is a set of elements called nodes, vertices, points, or elements and is a set of pairs of subsets of . Each of these pairs is called an edge or hyperedge; the vertex subset is known as its tail or domain, and as its head or codomain.
The order of a hypergraph is the number of vertices in . The size of the hypergraph is the number of edges in . The order of an edge in a directed hypergraph is : that is, the number of vertices in its tail followed by the number of vertices in its head.
The definition above generalizes from a directed graph to a directed hypergraph by defining the head or tail of each edge as a set of vertices ( or ) rather than as a single vertex. A graph is then the special case where each of these sets contains only one element. Hence any standard graph theoretic concept that is independent of the edge orders will generalize to hypergraph theory.
An undirected hypergraph is an undirected graph whose edges connect not just two vertices, but an arbitrary number.[2] An undirected hypergraph is also called a set system or a family of sets drawn from the universal set.
Hypergraphs can be viewed as incidence structures. In particular, there is a bipartite "incidence graph" or "Levi graph" corresponding to every hypergraph, and conversely, every bipartite graph can be regarded as the incidence graph of a hypergraph when it is 2-colored and it is indicated which color class corresponds to hypergraph vertices and which to hypergraph edges.
Hypergraphs have many other names. In computational geometry, an undirected hypergraph may sometimes be called a range space and then the hyperedges are called ranges.[3] In cooperative game theory, hypergraphs are called simple games (voting games); this notion is applied to solve problems in social choice theory. In some literature edges are referred to as hyperlinks or connectors.[4]
The collection of hypergraphs is a category with hypergraph homomorphisms as morphisms.
Remove ads
Applications
Summarize
Perspective
Undirected hypergraphs are useful in modelling such things as satisfiability problems,[5] databases,[6] machine learning,[7] and Steiner tree problems.[8] They have been extensively used in machine learning tasks as the data model and classifier regularization (mathematics).[9] The applications include recommender system (communities as hyperedges),[10][11] image retrieval (correlations as hyperedges),[12] and bioinformatics (biochemical interactions as hyperedges).[13] Representative hypergraph learning techniques include hypergraph spectral clustering that extends the spectral graph theory with hypergraph Laplacian,[14] and hypergraph semi-supervised learning that introduces extra hypergraph structural cost to restrict the learning results.[15] For large scale hypergraphs, a distributed framework[7] built using Apache Spark is also available. It can be desirable to study hypergraphs where all hyperedges have the same cardinality; a k-uniform hypergraph is a hypergraph such that all its hyperedges have size k. (In other words, one such hypergraph is a collection of sets, each such set a hyperedge connecting k nodes.) So a 2-uniform hypergraph is a graph, a 3-uniform hypergraph is a collection of unordered triples, and so on.
Directed hypergraphs can be used to model things including telephony applications,[16] detecting money laundering,[17] operations research,[18] and transportation planning. They can also be used to model Horn-satisfiability.[19]
Remove ads
Generalizations of concepts from graphs
Many theorems and concepts involving graphs also hold for hypergraphs, in particular:
- Matching in hypergraphs;
- Vertex cover in hypergraphs (also known as: transversal);
- Line graph of a hypergraph;
- Hypergraph grammar - created by augmenting a class of hypergraphs with a set of replacement rules;
- Ramsey's theorem;
- Erdős–Ko–Rado theorem;
- Kruskal–Katona theorem on uniform hypergraphs;
- Hall-type theorems for hypergraphs.
In directed hypergraphs: transitive closure, and shortest path problems.[18]
Remove ads
Hypergraph drawing
Summarize
Perspective

Although hypergraphs are more difficult to draw on paper than graphs, several researchers have studied methods for the visualization of hypergraphs.
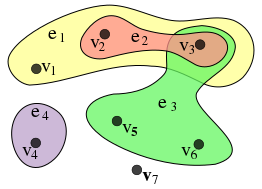
In one possible visual representation for hypergraphs, similar to the standard graph drawing style in which curves in the plane are used to depict graph edges, a hypergraph's vertices are depicted as points, disks, or boxes, and its hyperedges are depicted as trees that have the vertices as their leaves.[20][21] If the vertices are represented as points, the hyperedges may also be shown as smooth curves that connect sets of points, or as simple closed curves that enclose sets of points.[22][23][24]

In another style of hypergraph visualization, the subdivision model of hypergraph drawing,[25] the plane is subdivided into regions, each of which represents a single vertex of the hypergraph. The hyperedges of the hypergraph are represented by contiguous subsets of these regions, which may be indicated by coloring, by drawing outlines around them, or both. An order-n Venn diagram, for instance, may be viewed as a subdivision drawing of a hypergraph with n hyperedges (the curves defining the diagram) and 2n − 1 vertices (represented by the regions into which these curves subdivide the plane). In contrast with the polynomial-time recognition of planar graphs, it is NP-complete to determine whether a hypergraph has a planar subdivision drawing,[26] but the existence of a drawing of this type may be tested efficiently when the adjacency pattern of the regions is constrained to be a path, cycle, or tree.[27]
An alternative representation of the hypergraph called PAOH[1] is shown in the figure on top of this article. Edges are vertical lines connecting vertices. Vertices are aligned on the left. The legend on the right shows the names of the edges. It has been designed for dynamic hypergraphs but can be used for simple hypergraphs as well.
Remove ads
Hypergraph coloring
Summarize
Perspective
Classic hypergraph coloring is assigning one of the colors from set to every vertex of a hypergraph in such a way that each hyperedge contains at least two vertices of distinct colors. In other words, there must be no monochromatic hyperedge with cardinality at least 2. In this sense it is a direct generalization of graph coloring. The minimum number of used distinct colors over all colorings is called the chromatic number of a hypergraph.
Hypergraphs for which there exists a coloring using up to k colors are referred to as k-colorable. The 2-colorable hypergraphs are exactly the bipartite ones.
There are many generalizations of classic hypergraph coloring. One of them is the so-called mixed hypergraph coloring, when monochromatic edges are allowed. Some mixed hypergraphs are uncolorable for any number of colors. A general criterion for uncolorability is unknown. When a mixed hypergraph is colorable, then the minimum and maximum number of used colors are called the lower and upper chromatic numbers respectively.[28]
Remove ads
Properties of hypergraphs
Summarize
Perspective
A hypergraph can have various properties, such as:
- Empty - has no edges.
- Non-simple (or multiple) - has loops (hyperedges with a single vertex) or repeated edges, which means there can be two or more edges containing the same set of vertices.
- Simple - has no loops and no repeated edges.
- -regular - every vertex has degree , i.e., contained in exactly hyperedges.
- 2-colorable - its vertices can be partitioned into two classes U and V in such a way that each hyperedge with cardinality at least 2 contains at least one vertex from both classes. An alternative term is Property B.
- -uniform - each hyperedge contains precisely vertices.
- -partite - the vertices are partitioned into parts, and each hyperedge contains precisely one vertex of each type.
- Every -partite hypergraph (for ) is both -uniform and bipartite (and 2-colorable).
- Reduced:[29] no hyperedge is a strict subset of another hyperedge; equivalently, every hyperedge is maximal for inclusion. The reduction of a hypergraph is the reduced hypergraph obtained by removing every hyperedge which is included in another hyperedge.
- Downward-closed - every subset of an undirected hypergraph's edges is a hyperedge too. A downward-closed hypergraph is usually called an abstract simplicial complex. It is generally not reduced, unless all hyperedges have cardinality 1.
- An abstract simplicial complex with the augmentation property is called a matroid.
- Laminar: for any two hyperedges, either they are disjoint, or one is included in the other. In other words, the set of hyperedges forms a laminar set family.
Remove ads
Related hypergraphs
Summarize
Perspective
Because hypergraph links can have any cardinality, there are several notions of the concept of a subgraph, called subhypergraphs, partial hypergraphs and section hypergraphs.
Let be the hypergraph consisting of vertices
and having edge set
where and are the index sets of the vertices and edges respectively.
A subhypergraph is a hypergraph with some vertices removed. Formally, the subhypergraph induced by is defined as
An alternative term is the restriction of H to A.[30]: 468
An extension of a subhypergraph is a hypergraph where each hyperedge of which is partially contained in the subhypergraph is fully contained in the extension . Formally
- with and .
The partial hypergraph is a hypergraph with some edges removed.[30]: 468 Given a subset of the edge index set, the partial hypergraph generated by is the hypergraph
Given a subset , the section hypergraph is the partial hypergraph
The dual of is a hypergraph whose vertices and edges are interchanged, so that the vertices are given by and whose edges are given by where
When a notion of equality is properly defined, as done below, the operation of taking the dual of a hypergraph is an involution, i.e.,
A connected graph G with the same vertex set as a connected hypergraph H is a host graph for H if every hyperedge of H induces a connected subgraph in G. For a disconnected hypergraph H, G is a host graph if there is a bijection between the connected components of G and of H, such that each connected component G' of G is a host of the corresponding H'.
The 2-section (or clique graph, representing graph, primal graph, Gaifman graph) of a hypergraph is the graph with the same vertices of the hypergraph, and edges between all pairs of vertices contained in the same hyperedge.
Remove ads
Incidence matrix
Summarize
Perspective
Let and . Every hypergraph has an incidence matrix.
For an undirected hypergraph, where
The transpose of the incidence matrix defines a hypergraph called the dual of , where is an m-element set and is an n-element set of subsets of . For and if and only if .
For a directed hypergraph, the heads and tails of each hyperedge are denoted by and respectively.[19] where
Incidence graph
A hypergraph H may be represented by a bipartite graph BG as follows: the sets X and E are the parts of BG, and (x1, e1) are connected with an edge if and only if vertex x1 is contained in edge e1 in H.
Conversely, any bipartite graph with fixed parts and no unconnected nodes in the second part represents some hypergraph in the manner described above. This bipartite graph is also called incidence graph.
Remove ads
Adjacency matrix
A parallel for the adjacency matrix of a hypergraph can be drawn from the adjacency matrix of a graph. In the case of a graph, the adjacency matrix is a square matrix which indicates whether pairs of vertices are adjacent. Likewise, we can define the adjacency matrix for a hypergraph in general where the hyperedges have real weights with
Remove ads
Cycles
Summarize
Perspective
In contrast with ordinary undirected graphs for which there is a single natural notion of cycles and acyclic graphs. For hypergraphs, there are multiple natural non-equivalent definitions of cycles which collapse to the ordinary notion of cycle when the graph case is considered.
Berge cycles
A first notion of cycle was introduced by Claude Berge.[31] A Berge cycle in a hypergraph is an alternating sequence of distinct vertices and edges , where and are both in for each (with indices taken modulo ).
Under this definition a hypergraph is acyclic if and only if its incidence graph (the bipartite graph defined above) is acyclic. Thus Berge-cyclicity can obviously be tested in linear time by an exploration of the incidence graph.
Tight cycles
This definition is particularly used for -uniform hypergraphs, where all hyperedges are of size . A tight cycle of length in a hypergraph is a sequence of distinct vertices such that every consecutive -tuple (indices modulo ) forms a hyperedge in . This notion was introduced by Katona and Kierstead[32] and has since garnered considerable attention, particularly in the study of Hamiltonicity in extremal combinatorics.[33][34]
Rödl, Szemerédi, and Ruciński showed that every -vertex -uniform hypergraph in which every -subset of vertices is contained in at least hyperedges contains a Hamilton cycle. This corresponds to an approximate hypergraph-extension of the celebrated Dirac's theorem about Hamilton cycles in graphs.[35]
The maximum number of hyperedges in a (tightly) acyclic -uniform hypergraph remains unknown. The best known bounds, obtained by Sudakov and Tomon,[36] show that every -vertex -uniform hypergraph with at least hyperedges must contain a tight cycle. This bound is optimal up to the error term.
An -cycle generalizes the notion of a tight cycle. It consists in a sequence of vertices and hyperedges where each consists of consecutive vertices in the sequence and for every . Since every edge of the -cycle contains exactly vertices which are not contained in the previous edge, must be divisible by . Note that recovers the definition of a tight cycle.
α-acyclicity
The definition of Berge-acyclicity might seem to be very restrictive: for instance, if a hypergraph has some pair of vertices and some pair of hyperedges such that and , then it is Berge-cyclic.
We can define a weaker notion of hypergraph acyclicity,[6] later termed α-acyclicity. This notion of acyclicity is equivalent to the hypergraph being conformal (every clique of the primal graph is covered by some hyperedge) and its primal graph being chordal; it is also equivalent to reducibility to the empty graph through the GYO algorithm[37][38] (also known as Graham's algorithm), a confluent iterative process which removes hyperedges using a generalized definition of ears. In the domain of database theory, it is known that a database schema enjoys certain desirable properties if its underlying hypergraph is α-acyclic.[39] Besides, α-acyclicity is also related to the expressiveness of the guarded fragment of first-order logic.
We can test in linear time if a hypergraph is α-acyclic.[40]
Note that α-acyclicity has the counter-intuitive property that adding hyperedges to an α-cyclic hypergraph may make it α-acyclic (for instance, adding a hyperedge containing all vertices of the hypergraph will always make it α-acyclic). Motivated in part by this perceived shortcoming, Ronald Fagin[41] defined the stronger notions of β-acyclicity and γ-acyclicity. We can state β-acyclicity as the requirement that all subhypergraphs of the hypergraph are α-acyclic, which is equivalent[41] to an earlier definition by Graham.[38] The notion of γ-acyclicity is a more restrictive condition which is equivalent to several desirable properties of database schemas and is related to Bachman diagrams. Both β-acyclicity and γ-acyclicity can be tested in polynomial time.
Those four notions of acyclicity are comparable: γ-acyclicity which implies β-acyclicity which implies α-acyclicity. Moreover, Berge-acyclicity implies all of them. None of the reverse implications hold including the Berge one. In other words, these four notions are different.[41]
Remove ads
Isomorphism, symmetry, and equality
Summarize
Perspective
A hypergraph homomorphism is a map from the vertex set of one hypergraph to another such that each edge maps to one other edge.
A hypergraph is isomorphic to a hypergraph , written as if there exists a bijection
and a permutation of such that
The bijection is then called the isomorphism of the graphs. Note that
- if and only if .
When the edges of a hypergraph are explicitly labeled, one has the additional notion of strong isomorphism. One says that is strongly isomorphic to if the permutation is the identity. One then writes . Note that all strongly isomorphic graphs are isomorphic, but not vice versa.
When the vertices of a hypergraph are explicitly labeled, one has the notions of equivalence, and also of equality. One says that is equivalent to , and writes if the isomorphism has
and
Note that
- if and only if
If, in addition, the permutation is the identity, one says that equals , and writes . Note that, with this definition of equality, graphs are self-dual:
A hypergraph automorphism is an isomorphism from a vertex set into itself, that is a relabeling of vertices. The set of automorphisms of a hypergraph H (= (X, E)) is a group under composition, called the automorphism group of the hypergraph and written Aut(H).
Examples
Consider the hypergraph with edges
and
Then clearly and are isomorphic (with , etc.), but they are not strongly isomorphic. So, for example, in , vertex meets edges 1, 4 and 6, so that,
In graph , there does not exist any vertex that meets edges 1, 4 and 6:
In this example, and are equivalent, , and the duals are strongly isomorphic: .
Symmetry
The rank of a hypergraph is the maximum cardinality of any of the edges in the hypergraph. If all edges have the same cardinality k, the hypergraph is said to be uniform or k-uniform, or is called a k-hypergraph. A graph is just a 2-uniform hypergraph.
The degree d(v) of a vertex v is the number of edges that contain it. H is k-regular if every vertex has degree k.
The dual of a uniform hypergraph is regular and vice versa.
Two vertices x and y of H are called symmetric if there exists an automorphism such that . Two edges and are said to be symmetric if there exists an automorphism such that .
A hypergraph is said to be vertex-transitive (or vertex-symmetric) if all of its vertices are symmetric. Similarly, a hypergraph is edge-transitive if all edges are symmetric. If a hypergraph is both edge- and vertex-symmetric, then the hypergraph is simply transitive.
Because of hypergraph duality, the study of edge-transitivity is identical to the study of vertex-transitivity.
Remove ads
Partitions
Summarize
Perspective
A partition theorem due to E. Dauber[42] states that, for an edge-transitive hypergraph , there exists a partition
of the vertex set such that the subhypergraph generated by is transitive for each , and such that
where is the rank of H.
As a corollary, an edge-transitive hypergraph that is not vertex-transitive is bicolorable.
Graph partitioning (and in particular, hypergraph partitioning) has many applications to IC design[43] and parallel computing.[44][45][46] Efficient and scalable hypergraph partitioning algorithms are also important for processing large scale hypergraphs in machine learning tasks.[7]
Remove ads
Further generalizations
Summarize
Perspective
One possible generalization of a hypergraph is to allow edges to point at other edges.[47] There are two variations of this generalization. In one, the edges consist not only of a set of vertices, but may also contain subsets of vertices, subsets of subsets of vertices and so on ad infinitum. In essence, every edge is just an internal node of a tree or directed acyclic graph, and vertices are the leaf nodes. A hypergraph is then just a collection of trees with common, shared nodes (that is, a given internal node or leaf may occur in several different trees).[48][49] Conversely, every collection of trees can be understood as this generalized hypergraph. Since trees are widely used throughout computer science and many other branches of mathematics, one could say that hypergraphs appear naturally as well.[50] So, for example, this generalization arises naturally as a model of term algebra; edges correspond to terms and vertices correspond to constants or variables.[51]
For such a hypergraph, set membership then provides an ordering, but the ordering is neither a partial order nor a preorder, since it is not transitive.[52][53] The graph corresponding to the Levi graph of this generalization is a directed acyclic graph.[54] Consider, for example, the generalized hypergraph whose vertex set is and whose edges are and . Then, although and , it is not true that . However, the transitive closure of set membership for such hypergraphs does induce a partial order, and "flattens" the hypergraph into a partially ordered set.[55]
Alternately, edges can be allowed to point at other edges, irrespective of the requirement that the edges be ordered as directed, acyclic graphs.[47][48] This allows graphs with edge-loops, which need not contain vertices at all. For example, consider the generalized hypergraph consisting of two edges and , and zero vertices, so that and . As this loop is infinitely recursive, sets that are the edges violate the axiom of foundation.[48] In particular, there is no transitive closure of set membership for such hypergraphs. Although such structures may seem strange at first, they can be readily understood by noting that the equivalent generalization of their Levi graph is no longer bipartite, but is rather just some general directed graph.[56]
The generalized incidence matrix for such hypergraphs is, by definition, a square matrix, of a rank equal to the total number of vertices plus edges.[57] Thus, for the above example, the incidence matrix is simply
- .
See also
Wikimedia Commons has media related to Hypergraphs.
- BF-graph – Type of directed hypergraph
- Combinatorial design – Symmetric arrangement of finite sets
- Factor graph – Function graph representing factorization
- Greedoid – Set system used in greedy optimization
- Incidence structure – Abstract mathematical system of two types of objects and a relation between them
- Multigraph – Graph with multiple edges between two vertices
- P system – Computational model
- Sparse matrix–vector multiplication – Computation routine
- Petri Net – Model to describe distributed systems
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads











































































![{\displaystyle i\in [n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1b389a8f1ad8a43d2bcf5194acf34e934f806311)
























































![{\displaystyle \left[{\begin{matrix}0&1\\1&0\end{matrix}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d81d2118440d37d41d43997b5e42fa1bac50e03b)