Top Qs
Timeline
Chat
Perspective
Interval arithmetic
Method for bounding the errors of numerical computations From Wikipedia, the free encyclopedia
Remove ads
Interval arithmetic (also known as interval mathematics; interval analysis or interval computation) is a mathematical technique used to mitigate rounding and measurement errors in mathematical computation by computing function bounds. Numerical methods involving interval arithmetic can guarantee relatively reliable and mathematically correct results. Instead of representing a value as a single number, interval arithmetic or interval mathematics represents each value as a range of possibilities.
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
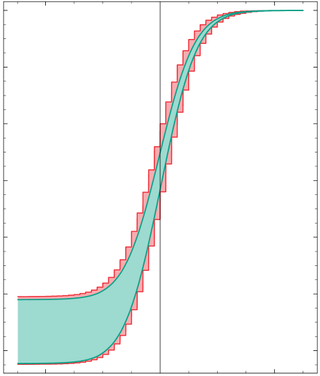
Mathematically, instead of working with an uncertain real-valued variable , interval arithmetic works with an interval that defines the range of values that can have. In other words, any value of the variable lies in the closed interval between and . A function , when applied to , produces an interval which includes all the possible values for for all .
Interval arithmetic is suitable for a variety of purposes; the most common use is in scientific works, particularly when the calculations are handled by software, where it is used to keep track of rounding errors in calculations and of uncertainties in the knowledge of the exact values of physical and technical parameters. The latter often arise from measurement errors and tolerances for components or due to limits on computational accuracy. Interval arithmetic also helps find guaranteed solutions to equations (such as differential equations) and optimization problems.
Remove ads
Introduction
Summarize
Perspective
The main objective of interval arithmetic is to provide a simple way of calculating upper and lower bounds of a function's range in one or more variables. These endpoints are not necessarily the true supremum or infimum of a range since the precise calculation of those values can be difficult or impossible; the bounds only need to contain the function's range as a subset.
This treatment is typically limited to real intervals, so quantities in the form
where and are allowed. With one of , infinite, the interval would be an unbounded interval; with both infinite, the interval would be the extended real number line. Since a real number can be interpreted as the interval intervals and real numbers can be freely combined.
Example

Consider the calculation of a person's body mass index (BMI). BMI is calculated as a person's body weight in kilograms divided by the square of their height in meters. Suppose a person uses a scale that has a precision of one kilogram, where intermediate values cannot be discerned, and the true weight is rounded to the nearest whole number. For example, 79.6 kg and 80.3 kg are indistinguishable, as the scale can only display values to the nearest kilogram. It is unlikely that when the scale reads 80 kg, the person has a weight of exactly 80.0 kg. Thus, the scale displaying 80 kg indicates a weight between 79.5 kg and 80.5 kg, or the interval .
The BMI of a man who weighs 80 kg and is 1.80m tall is approximately 24.7. A weight of 79.5 kg and the same height yields a BMI of 24.537, while a weight of 80.5 kg yields 24.846. Since the body mass is continuous and always increasing for all values within the specified weight interval, the true BMI must lie within the interval . Since the entire interval is less than 25, which is the cutoff between normal and excessive weight, it can be concluded with certainty that the man is of normal weight.
The error in this example does not affect the conclusion (normal weight), but this is not generally true. If the man were slightly heavier, the BMI's range may include the cutoff value of 25. In such a case, the scale's precision would be insufficient to make a definitive conclusion.
The range of BMI examples could be reported as since this interval is a superset of the calculated interval. The range could not, however, be reported as , as the interval does not contain possible BMI values.
Multiple intervals

Height and body weight both affect the value of the BMI. Though the example above only considered variation in weight, height is also subject to uncertainty. Height measurements in meters are usually rounded to the nearest centimeter: a recorded measurement of 1.79 meters represents a height in the interval . Since the BMI uniformly increases with respect to weight and decreases with respect to height, the error interval can be calculated by substituting the lowest and highest values of each interval, and then selecting the lowest and highest results as boundaries. The BMI must therefore exist in the interval
In this case, the man may have normal weight or be overweight; the weight and height measurements were insufficiently precise to make a definitive conclusion.
Remove ads
Interval operators
Summarize
Perspective
A binary operation on two intervals, such as addition or multiplication is defined by
In other words, it is the set of all possible values of , where and are in their corresponding intervals. If is monotone for each operand on the intervals, which is the case for the four basic arithmetic operations (except division when the denominator contains ), the extreme values occur at the endpoints of the operand intervals. Writing out all combinations, one way of stating this is
provided that is defined for all and .
For practical applications, this can be simplified further:
- Addition:
- Subtraction:
- Multiplication:
- Division: where
The last case loses useful information about the exclusion of . Thus, it is common to work with and as separate intervals. More generally, when working with discontinuous functions, it is sometimes useful to do the calculation with so-called multi-intervals of the form The corresponding multi-interval arithmetic maintains a set of (usually disjoint) intervals and also provides for overlapping intervals to unite.[1]

Interval multiplication often only requires two multiplications. If , are nonnegative,
The multiplication can be interpreted as the area of a rectangle with varying edges. The result interval covers all possible areas, from the smallest to the largest.
With the help of these definitions, it is already possible to calculate the range of simple functions, such as For example, if , and :
Notation
To shorten the notation of intervals, brackets can be used.
can be used to represent an interval. Note that in such a compact notation, should not be confused between a single-point interval and a general interval. For the set of all intervals, we can use
as an abbreviation. For a vector of intervals we can use a bold font: .
Elementary functions

Interval functions beyond the four basic operators may also be defined.
For monotonic functions in one variable, the range of values is simple to compute. If is monotonically increasing (resp. decreasing) in the interval then for all such that (resp. ).
The range corresponding to the interval can be therefore calculated by applying the function to its endpoints:
From this, the following basic features for interval functions can easily be defined:
- Exponential function: for
- Logarithm: for positive intervals and
- Odd powers: , for odd
For even powers, the range of values being considered is important and needs to be dealt with before doing any multiplication. For example, for should produce the interval when But if is taken by repeating interval multiplication of form then the result is wider than necessary.
More generally one can say that, for piecewise monotonic functions, it is sufficient to consider the endpoints , of an interval, together with the so-called critical points within the interval, being those points where the monotonicity of the function changes direction. For the sine and cosine functions, the critical points are at or for , respectively. Thus, only up to five points within an interval need to be considered, as the resulting interval is if the interval includes at least two extrema. For sine and cosine, only the endpoints need full evaluation, as the critical points lead to easily pre-calculated values—namely −1, 0, and 1.
Interval extensions of general functions
In general, it may not be easy to find such a simple description of the output interval for many functions. But it may still be possible to extend functions to interval arithmetic. If is a function from a real vector to a real number, then is called an interval extension of if
This definition of the interval extension does not give a precise result. For example, both and are allowable extensions of the exponential function. Tighter extensions are desirable, though the relative costs of calculation and imprecision should be considered; in this case, should be chosen as it gives the tightest possible result.
Given a real expression, its natural interval extension is achieved by using the interval extensions of each of its subexpressions, functions, and operators.
The Taylor interval extension (of degree ) is a times differentiable function defined by
for some , where is the -th order differential of at the point and is an interval extension of the Taylor remainder.

The vector lies between and with , is protected by . Usually one chooses to be the midpoint of the interval and uses the natural interval extension to assess the remainder.
The special case of the Taylor interval extension of degree is also referred to as the mean value form.
Remove ads
Complex interval arithmetic
Summarize
Perspective
An interval can be defined as a set of points within a specified distance of the center, and this definition can be extended from real numbers to complex numbers.[2] Another extension defines intervals as rectangles in the complex plane. As is the case with computing with real numbers, computing with complex numbers involves uncertain data. So, given the fact that an interval number is a real closed interval and a complex number is an ordered pair of real numbers, there is no reason to limit the application of interval arithmetic to the measure of uncertainties in computations with real numbers.[3] Interval arithmetic can thus be extended, via complex interval numbers, to determine regions of uncertainty in computing with complex numbers. One can either define complex interval arithmetic using rectangles or using disks, both with their respective advantages and disadvantages.[3]
The basic algebraic operations for real interval numbers (real closed intervals) can be extended to complex numbers. It is therefore not surprising that complex interval arithmetic is similar to, but not the same as, ordinary complex arithmetic.[3] It can be shown that, as is the case with real interval arithmetic, there is no distributivity between the addition and multiplication of complex interval numbers except for certain special cases, and inverse elements do not always exist for complex interval numbers.[3] Two other useful properties of ordinary complex arithmetic fail to hold in complex interval arithmetic: the additive and multiplicative properties, of ordinary complex conjugates, do not hold for complex interval conjugates.[3]
Interval arithmetic can be extended, in an analogous manner, to other multidimensional number systems such as quaternions and octonions, but with the expense that we have to sacrifice other useful properties of ordinary arithmetic.[3]
Interval methods
Summarize
Perspective
This section needs additional citations for verification. (February 2018) |
The methods of classical numerical analysis cannot be transferred one-to-one into interval-valued algorithms, as dependencies between numerical values are usually not taken into account.
Rounded interval arithmetic

To work effectively in a real-life implementation, intervals must be compatible with floating point computing. The earlier operations were based on exact arithmetic, but in general fast numerical solution methods may not be available for it. The range of values of the function for and are for example . Where the same calculation is done with single-digit precision, the result would normally be . But , so this approach would contradict the basic principles of interval arithmetic, as a part of the domain of would be lost. Instead, the outward rounded solution is used.
The standard IEEE 754 for binary floating-point arithmetic also sets out procedures for the implementation of rounding. An IEEE 754 compliant system allows programmers to round to the nearest floating-point number; alternatives are rounding towards 0 (truncating), rounding toward positive infinity (i.e., up), or rounding towards negative infinity (i.e., down).
The required external rounding for interval arithmetic can thus be achieved by changing the rounding settings of the processor in the calculation of the upper limit (up) and lower limit (down). Alternatively, an appropriate small interval can be added.
Dependency problem

The so-called "dependency" problem is a major obstacle to the application of interval arithmetic. Although interval methods can determine the range of elementary arithmetic operations and functions very accurately, this is not always true with more complicated functions. If an interval occurs several times in a calculation using parameters, and each occurrence is taken independently, then this can lead to an unwanted expansion of the resulting intervals.

As an illustration, take the function defined by The values of this function over the interval are As the natural interval extension, it is calculated as:
which is slightly larger; we have instead calculated the infimum and supremum of the function over There is a better expression of in which the variable only appears once, namely by rewriting as addition and squaring in the quadratic.
So the suitable interval calculation is
and gives the correct values.
In general, it can be shown that the exact range of values can be achieved, if each variable appears only once and if is continuous inside the box. However, not every function can be rewritten this way.

The dependency of the problem causing over-estimation of the value range can go as far as covering a large range, preventing more meaningful conclusions.
An additional increase in the range stems from the solution of areas that do not take the form of an interval vector. The solution set of the linear system
is precisely the line between the points and Using interval methods results in the unit square, This is known as the wrapping effect.
Linear interval systems
A linear interval system consists of a matrix interval extension and an interval vector . We want the smallest cuboid , for all vectors which there is a pair with and satisfying.
- .
For quadratic systems – in other words, for – there can be such an interval vector , which covers all possible solutions, found simply with the interval Gauss method. This replaces the numerical operations, in that the linear algebra method known as Gaussian elimination becomes its interval version. However, since this method uses the interval entities and repeatedly in the calculation, it can produce poor results for some problems. Hence using the result of the interval-valued Gauss only provides first rough estimates, since although it contains the entire solution set, it also has a large area outside it.
A rough solution can often be improved by an interval version of the Gauss–Seidel method. The motivation for this is that the -th row of the interval extension of the linear equation.
can be determined by the variable if the division is allowed. It is therefore simultaneously.
- and .
So we can now replace by
- ,
and so the vector by each element. Since the procedure is more efficient for a diagonally dominant matrix, instead of the system one can often try multiplying it by an appropriate rational matrix with the resulting matrix equation.
left to solve. If one chooses, for example, for the central matrix , then is outer extension of the identity matrix.
These methods only work well if the widths of the intervals occurring are sufficiently small. For wider intervals, it can be useful to use an interval-linear system on finite (albeit large) real number equivalent linear systems. If all the matrices are invertible, it is sufficient to consider all possible combinations (upper and lower) of the endpoints occurring in the intervals. The resulting problems can be resolved using conventional numerical methods. Interval arithmetic is still used to determine rounding errors.
This is only suitable for systems of smaller dimension, since with a fully occupied matrix, real matrices need to be inverted, with vectors for the right-hand side. This approach was developed by Jiri Rohn and is still being developed.[4]
Interval Newton method

An interval variant of Newton's method for finding the zeros in an interval vector can be derived from the average value extension.[5] For an unknown vector applied to , gives.
- .
For a zero , that is , and thus, must satisfy.
- .
This is equivalent to . An outer estimate of can be determined using linear methods.
In each step of the interval Newton method, an approximate starting value is replaced by and so the result can be improved. In contrast to traditional methods, the interval method approaches the result by containing the zeros. This guarantees that the result produces all zeros in the initial range. Conversely, it proves that no zeros of were in the initial range if a Newton step produces the empty set.
The method converges on all zeros in the starting region. Division by zero can lead to the separation of distinct zeros, though the separation may not be complete; it can be complemented by the bisection method.
As an example, consider the function , the starting range , and the point . We then have and the first Newton step gives.
- .
More Newton steps are used separately on and . These converge to arbitrarily small intervals around and .
The Interval Newton method can also be used with thick functions such as , which would in any case have interval results. The result then produces intervals containing .
Bisection and covers

The various interval methods deliver conservative results as dependencies between the sizes of different interval extensions are not taken into account. However, the dependency problem becomes less significant for narrower intervals.
Covering an interval vector by smaller boxes so that
is then valid for the range of values.
So, for the interval extensions described above the following holds:
Since is often a genuine superset of the right-hand side, this usually leads to an improved estimate.
Such a cover can be generated by the bisection method such as thick elements of the interval vector by splitting in the center into the two intervals and If the result is still not suitable then further gradual subdivision is possible. A cover of intervals results from divisions of vector elements, substantially increasing the computation costs.
With very wide intervals, it can be helpful to split all intervals into several subintervals with a constant (and smaller) width, a method known as mincing. This then avoids the calculations for intermediate bisection steps. Both methods are only suitable for problems of low dimension.
Remove ads
Application
Summarize
Perspective
Interval arithmetic can be used in various areas (such as set inversion, motion planning, set estimation, or stability analysis) to treat estimates with no exact numerical value.[6]
Rounding error analysis
Interval arithmetic is used with error analysis, to control rounding errors arising from each calculation. The advantage of interval arithmetic is that after each operation there is an interval that reliably includes the true result. The distance between the interval boundaries gives the current calculation of rounding errors directly:
- Error = for a given interval .
Interval analysis adds to rather than substituting for traditional methods for error reduction, such as pivoting.
Tolerance analysis
Parameters for which no exact figures can be allocated often arise during the simulation of technical and physical processes. The production process of technical components allows certain tolerances, so some parameters fluctuate within intervals. In addition, many fundamental constants are not known precisely.[1]
If the behavior of such a system affected by tolerances satisfies, for example, , for and unknown then the set of possible solutions.
- ,
can be found by interval methods. This provides an alternative to traditional propagation of error analysis. Unlike point methods, such as Monte Carlo simulation, interval arithmetic methodology ensures that no part of the solution area can be overlooked. However, the result is always a worst-case analysis for the distribution of error, as other probability-based distributions are not considered.
Fuzzy interval arithmetic
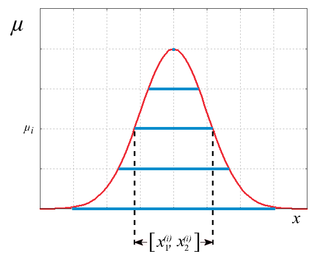
Interval arithmetic can also be used with affiliation functions for fuzzy quantities as they are used in fuzzy logic. Apart from the strict statements and , intermediate values are also possible, to which real numbers are assigned. corresponds to definite membership while is non-membership. A distribution function assigns uncertainty, which can be understood as a further interval.
For fuzzy arithmetic[7] only a finite number of discrete affiliation stages are considered. The form of such a distribution for an indistinct value can then be represented by a sequence of intervals.
The interval corresponds exactly to the fluctuation range for the stage
The appropriate distribution for a function concerning indistinct values and the corresponding sequences.
can be approximated by the sequence.
where
and can be calculated by interval methods. The value corresponds to the result of an interval calculation.
Computer-assisted proof
Warwick Tucker used interval arithmetic in order to solve the 14th of Smale's problems, that is, to show that the Lorenz attractor is a strange attractor.[8] Thomas Hales used interval arithmetic in order to solve the Kepler conjecture.
Remove ads
History
Summarize
Perspective
Interval arithmetic is not a completely new phenomenon in mathematics; it has appeared several times under different names in the course of history. For example, Archimedes calculated lower and upper bounds 223/71 < π < 22/7 in the 3rd century BC. Actual calculation with intervals has neither been as popular as other numerical techniques nor been completely forgotten.
Rules for calculating with intervals and other subsets of the real numbers were published in a 1931 work by Rosalind Cicely Young.[9] Arithmetic work on range numbers to improve the reliability of digital systems was then published in a 1951 textbook on linear algebra by Paul S. Dwyer;[10] intervals were used to measure rounding errors associated with floating-point numbers. A comprehensive paper on interval algebra in numerical analysis was published by Teruo Sunaga (1958).[11]
The birth of modern interval arithmetic was marked by the appearance of the book Interval Analysis by Ramon E. Moore in 1966.[12][13] He had the idea in spring 1958, and a year later he published an article about computer interval arithmetic.[14] Its merit was that starting with a simple principle, it provided a general method for automated error analysis, not just errors resulting from rounding.
Independently in 1956, Mieczyslaw Warmus suggested formulae for calculations with intervals,[15] though Moore found the first non-trivial applications.
In the following twenty years, German groups of researchers carried out pioneering work around Ulrich W. Kulisch[16][17] and Götz Alefeld[18] at the University of Karlsruhe and later also at the Bergische University of Wuppertal. For example, Karl Nickel explored more effective implementations, while improved containment procedures for the solution set of systems of equations were due to Arnold Neumaier among others. In the 1960s, Eldon R. Hansen dealt with interval extensions for linear equations and then provided crucial contributions to global optimization, including what is now known as Hansen's method, perhaps the most widely used interval algorithm.[5] Classical methods in this often have the problem of determining the largest (or smallest) global value, but could only find a local optimum and could not find better values; Helmut Ratschek and Jon George Rokne developed branch and bound methods, which until then had only applied to integer values, by using intervals to provide applications for continuous values.
In 1988, Rudolf Lohner developed Fortran-based software for reliable solutions for initial value problems using ordinary differential equations.[19]
The journal Reliable Computing (originally Interval Computations) has been published since the 1990s, dedicated to the reliability of computer-aided computations. As lead editor, R. Baker Kearfott, in addition to his work on global optimization, has contributed significantly to the unification of notation and terminology used in interval arithmetic.[20]
In recent years work has concentrated in particular on the estimation of preimages of parameterized functions and to robust control theory by the COPRIN working group of INRIA in Sophia Antipolis in France.[21]
Remove ads
Implementations
Summarize
Perspective
There are many software packages that permit the development of numerical applications using interval arithmetic.[22] These are usually provided in the form of program libraries. There are also C++ and Fortran compilers that handle interval data types and suitable operations as a language extension, so interval arithmetic is supported directly.
Since 1967, Extensions for Scientific Computation (XSC) have been developed in the University of Karlsruhe for various programming languages, such as C++, Fortran, and Pascal.[23] The first platform was a Zuse Z23, for which a new interval data type with appropriate elementary operators was made available. There followed in 1976, Pascal-SC, a Pascal variant on a Zilog Z80 that it made possible to create fast, complicated routines for automated result verification. Then came the Fortran 77-based ACRITH-XSC for the System/370 architecture (FORTRAN-SC), which was later delivered by IBM. Starting from 1991 one could produce code for C compilers with Pascal-XSC; a year later the C++ class library supported C-XSC on many different computer systems. In 1997, all XSC variants were made available under the GNU General Public License. At the beginning of 2000, C-XSC 2.0 was released under the leadership of the working group for scientific computation at the Bergische University of Wuppertal to correspond to the improved C++ standard.
Another C++-class library was created in 1993 at the Hamburg University of Technology called Profil/BIAS (Programmer's Runtime Optimized Fast Interval Library, Basic Interval Arithmetic), which made the usual interval operations more user-friendly. It emphasized the efficient use of hardware, portability, and independence of a particular presentation of intervals.
The Boost collection of C++ libraries contains a template class for intervals. Its authors are aiming to have interval arithmetic in the standard C++ language.[24]
The Frink programming language has an implementation of interval arithmetic that handles arbitrary-precision numbers. Programs written in Frink can use intervals without rewriting or recompilation.
GAOL[25] is another C++ interval arithmetic library that is unique in that it offers the relational interval operators used in interval constraint programming.
The Moore library[26] is an efficient implementation of interval arithmetic in C++. It provides intervals with endpoints of arbitrary precision and is based on the concepts feature of C++.
The Julia programming language[27] has an implementation of interval arithmetics along with high-level features, such as root-finding (for both real and complex-valued functions) and interval constraint programming, via the ValidatedNumerics.jl package.[28]
In addition, computer algebra systems, such as Euler Mathematical Toolbox, FriCAS, Maple, Mathematica, Maxima[29] and MuPAD, can handle intervals. A Matlab extension Intlab[30] builds on BLAS routines, and the toolbox b4m makes a Profil/BIAS interface.[30][31]
A library for the functional language OCaml was written in assembly language and C.[32]
MPFI is a library for arbitrary precision interval arithmetic; it is written in C and is based on MPFR.[33]
Remove ads
IEEE 1788 standard
A standard for interval arithmetic, IEEE Std 1788-2015, has been approved in June 2015.[34] Two reference implementations are freely available.[35] These have been developed by members of the standard's working group: The libieeep1788[36] library for C++, and the interval package[37] for GNU Octave.
A minimal subset of the standard, IEEE Std 1788.1-2017, has been approved in December 2017 and published in February 2018. It should be easier to implement and may speed production of implementations.[38]
Remove ads
Conferences and workshops
Several international conferences or workshops take place every year in the world. The main conference is probably SCAN (International Symposium on Scientific Computing, Computer Arithmetic, and Verified Numerical Computation), but there is also SWIM (Small Workshop on Interval Methods), PPAM (International Conference on Parallel Processing and Applied Mathematics), REC (International Workshop on Reliable Engineering Computing).
See also
References
Further reading
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads


![{\displaystyle [a,b]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



![{\displaystyle [c,d]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d85b3b21d6d891d97f85e263d394e3c90287586f)

![{\displaystyle x\in [a,b]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)
![{\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\},}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e2d85d117bd54755bfca42ab82ad93bbfe40bd68)



![{\displaystyle [r,r],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2efd011cc6059ec2bd64f0748ba60dd2d6629d64)

![{\displaystyle [24.537,24.846]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4ff30647867964a66d0b1a12e235a7065ea978f8)
![{\displaystyle [24.5,24.9]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/06ab381403bf66d91e3f10be9e6c241fe7c1f030)
![{\displaystyle [24.6,24.8]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d5eae3c94ed832b32292750aa58853ba97d3387f)

![{\displaystyle {\frac {[79.5,80.5)}{[1.785,1.795)^{2}}}\subseteq [24.673,25.266].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/14168d8c36e9df3b187baf667c36901bbbc1c304)

![{\displaystyle [x_{1},x_{2}]{\,\star \,}[y_{1},y_{2}]=\{x\star y\,|\,x\in [x_{1},x_{2}]\,\land \,y\in [y_{1},y_{2}]\}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e5fba733818a68eef83c097c5702f671f15e9410)



![{\displaystyle [x_{1},x_{2}]\star [y_{1},y_{2}]=\left[\min\{x_{1}\star y_{1},x_{1}\star y_{2},x_{2}\star y_{1},x_{2}\star y_{2}\},\max\{x_{1}\star y_{1},x_{1}\star y_{2},x_{2}\star y_{1},x_{2}\star y_{2}\}\right],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2bf8c2437a98abc2860242a2f252960055cc7a2f)
![{\displaystyle x\in [x_{1},x_{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/28267d22f13c327a49b44a9cb3f3e4cd38b39d13)
![{\displaystyle y\in [y_{1},y_{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/31a0372448736f80721f3afb4a8d3116d7e060bb)
![{\displaystyle [x_{1},x_{2}]+[y_{1},y_{2}]=[x_{1}+y_{1},x_{2}+y_{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3b542d7b116e1934f6f7cba9ef63333cc26a77e3)
![{\displaystyle [x_{1},x_{2}]-[y_{1},y_{2}]=[x_{1}-y_{2},x_{2}-y_{1}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/85c4d944e4f5856cca9f868e7f42649a5ef8d30f)
![{\displaystyle [x_{1},x_{2}]\cdot [y_{1},y_{2}]=[\min\{x_{1}y_{1},x_{1}y_{2},x_{2}y_{1},x_{2}y_{2}\},\max\{x_{1}y_{1},x_{1}y_{2},x_{2}y_{1},x_{2}y_{2}\}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7855be35a6ca223d6ef525ee4dc5a56e2e8b30fc)
![{\displaystyle {\frac {[x_{1},x_{2}]}{[y_{1},y_{2}]}}=[x_{1},x_{2}]\cdot {\frac {1}{[y_{1},y_{2}]}},}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1587a3bd99c9a574533aa4de686aec4ee5c7daa4)
![{\displaystyle {\begin{aligned}{\frac {1}{[y_{1},y_{2}]}}&=\left[{\tfrac {1}{y_{2}}},{\tfrac {1}{y_{1}}}\right]&&{\textrm {if}}\;0\notin [y_{1},y_{2}]\\{\frac {1}{[y_{1},0]}}&=\left[-\infty ,{\tfrac {1}{y_{1}}}\right]\\{\frac {1}{[0,y_{2}]}}&=\left[{\tfrac {1}{y_{2}}},\infty \right]\\{\frac {1}{[y_{1},y_{2}]}}&=\left[-\infty ,{\tfrac {1}{y_{1}}}\right]\cup \left[{\tfrac {1}{y_{2}}},\infty \right]\subseteq [-\infty ,\infty ]&&{\textrm {if}}\;0\in (y_{1},y_{2})\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7ed4e215dfe1ad86b7d8965cadc4511dadbbdcda)

![{\displaystyle \left[-\infty ,{\tfrac {1}{y_{1}}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/608ebabc02d50a19b01ae9c012da8b05bfbe8b7a)
![{\displaystyle \left[{\tfrac {1}{y_{2}}},\infty \right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/c32f946e77696fcbbd45d2d588f883433c5bb664)
![{\textstyle \bigcup _{i}\left[a_{i},b_{i}\right].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/01c36c4fd18f5e83e31b789181c3fe2e447775e8)


![{\displaystyle [x_{1},x_{2}]\cdot [y_{1},y_{2}]=[x_{1}\cdot y_{1},x_{2}\cdot y_{2}],\qquad {\text{ if }}x_{1},y_{1}\geq 0.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b4d00fd7d14ca5cdbd2357220f6aca866e0b665b)

![{\displaystyle a=[1,2]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/91790e08fd2f86a980cdb4c012455fb5fb088314)
![{\displaystyle b=[5,7]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/580945e531a2b49d3b1025da4ced2d04d3276151)
![{\displaystyle x=[2,3]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7eb8fd099786d42d5c8479cb22dcd6d1ca67da37)
![{\displaystyle f(a,b,x)=([1,2]\cdot [2,3])+[5,7]=[1\cdot 2,2\cdot 3]+[5,7]=[7,13].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/09d02417221adcebe7dc099780769c69f17b3477)
![{\displaystyle [x]\equiv [x_{1},x_{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1d322dcd67b7a0ab33a04094ffef417552119ad2)
![{\displaystyle [x]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
![{\displaystyle [x_{1},x_{1}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/41877bedc66b3761d2054384a30df5df95b3325f)
![{\displaystyle [\mathbb {R} ]:=\left\{\,[x_{1},x_{2}]\,|\,x_{1}\leq x_{2}{\text{ and }}x_{1},x_{2}\in \mathbb {R} \cup \{-\infty ,\infty \}\right\}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9c246d6579baaaa59be83c8d31e670ea1a334646)
![{\displaystyle \left([x]_{1},\ldots ,[x]_{n}\right)\in [\mathbb {R} ]^{n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5fb4b1fbe11a16a257ea7f976b25b3e95c65a56b)
![{\displaystyle [\mathbf {x} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4290e7f30dee955efaed120787cce1b1b5ec6134)

![{\displaystyle [x_{1},x_{2}],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5defe368e30e73e75fd4504401771929d987bdaf)
![{\displaystyle y_{1},y_{2}\in [x_{1},x_{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/85c34f3ed35814345d132f44de3a61839b756e4a)



![{\displaystyle [y_{1},y_{2}]\subseteq [x_{1},x_{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1ef787934d937f062fc74eb29f6871dc05ae5a45)
![{\displaystyle f([y_{1},y_{2}])=\left[\min \left\{f(y_{1}),f(y_{2})\right\},\max \left\{f(y_{1}),f(y_{2})\right\}\right].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5b107317a027aaa133789dfaf8a4396716669c8c)
![{\displaystyle a^{[x_{1},x_{2}]}=[a^{x_{1}},a^{x_{2}}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e0594eea6d7cc12e0eb0118e89cacab79fd4a2a2)

![{\displaystyle \log _{a}[x_{1},x_{2}]=[\log _{a}{x_{1}},\log _{a}{x_{2}}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/22436b0a8dd5eca509da0bd74e1bbbbe2a7ce1cb)
![{\displaystyle [x_{1},x_{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/91bdff343d848c2b70c68b5c04a2479b14a9fef0)
![{\displaystyle [x_{1},x_{2}]^{n}=[x_{1}^{n},x_{2}^{n}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/45d38090f258b7116adc87b9f4bc381e711bd882)


![{\displaystyle x\in [-1,1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1f9d0dda56ce3e01e14570ac9aef0021c6125722)
![{\displaystyle [0,1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

![{\displaystyle [-1,1]^{n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6a008254b1bf6d63ac3b13548c4c31180bcd43de)
![{\displaystyle [-1,1]\cdot [-1,1]\cdot \cdots \cdot [-1,1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5b98a51edda6114c7ec741d303142aab6d224235)
![{\displaystyle [-1,1],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d9c504e0d448149f190679df28cd10275a67f117)




![{\displaystyle [-1,1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

![{\displaystyle [f]:[\mathbb {R} ]^{n}\to [\mathbb {R} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/105e33f991d5df78e19b96969146e7115cf0a64d)
\supseteq \{f(\mathbf {y} )\mid \mathbf {y} \in [\mathbf {x} ]\}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0ee422972297c7120d85a1533dd3e17bef4832e0)
=[e^{x_{1}},e^{x_{2}}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9ec9868ed84cec7efa6b71b0dc58aebd5a9970ae)
=[{-\infty },{\infty }]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2810a06e16744b723a839880bd3dd5c0cb7e8513)
![{\displaystyle [f]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/7414a730e8157655ff770265ec3a03ec9f09dd54)


:=f(\mathbf {y} )+\sum _{i=1}^{k}{\frac {1}{i!}}\mathrm {D} ^{i}f(\mathbf {y} )\cdot ([\mathbf {x} ]-\mathbf {y} )^{i}+[r]([\mathbf {x} ],[\mathbf {x} ],\mathbf {y} ),}](http://wikimedia.org/api/rest_v1/media/math/render/svg/977a73887704b2ace42ef527a8fd9b67af036590)
![{\displaystyle \mathbf {y} \in [\mathbf {x} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/78f1514af17ca752389b762fc65be958264c1f61)



![{\displaystyle [r]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b2a2bcc2aac5f01558c1fdd11d9445b1a1ab2294)



![{\displaystyle \mathbf {x} ,\mathbf {y} \in [\mathbf {x} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2d95b0902ecdfb59cc8c8127bb16f2fae6d33cae)


![{\displaystyle x\in [0.1,0.8]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/689645ace34c3b6e8266162dcc1591e6fb3ba7d1)
![{\displaystyle y\in [0.06,0.08]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fe12861a4276e2175fd71428c2279e4834f92ea2)
![{\displaystyle [0.16,0.88]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ce52b11e69058574c41b7d7a0111c9ad9aeb182e)
![{\displaystyle [0.2,0.9]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4841eb06d21b3c8de579f92d49babeeafd381787)
![{\displaystyle [0.2,0.9]\not \supseteq [0.16,0.88]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a24db69c1a2225f9f802eb9de666f0cbbfec53f4)
![{\displaystyle f([0.1,0.8],[0.06,0.08])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/164f0d021f04b83091ad1a4ed9d4e17d0a4c8136)
![{\displaystyle [0.1,0.9]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/243b1393ad22916492e575454cb491886648126d)
![{\displaystyle [\varepsilon _{1},\varepsilon _{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fa4b406e59070d5f209fc7ff7926287216306872)

![{\displaystyle \left[-{\tfrac {1}{4}},2\right].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0d7f0b52e03a77dddd05731b5b4b06d3c8825e01)
![{\displaystyle [-1,1]^{2}+[-1,1]=[0,1]+[-1,1]=[-1,2],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/41ffaf0653d779a2646bc8f00e2d8fa77c9c6017)

![{\displaystyle x,y\in [-1,1].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ae115a8808761a6ea949db1d67311d2f7fceba0d)


![{\displaystyle \left([-1,1]+{\frac {1}{2}}\right)^{2}-{\frac {1}{4}}=\left[-{\frac {1}{2}},{\frac {3}{2}}\right]^{2}-{\frac {1}{4}}=\left[0,{\frac {9}{4}}\right]-{\frac {1}{4}}=\left[-{\frac {1}{4}},2\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/707b219564c10f6be71e82c3ee8def7719d79ec2)
![{\displaystyle {\begin{cases}x=p\\y=p\end{cases}}\qquad p\in [-1,1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/38c5d127b26a746c668379c1d87e9db43afc7298)


![{\displaystyle [-1,1]\times [-1,1].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d08df9b71763a4652da60cc02a6202a31cb5cd86)
![{\displaystyle [\mathbf {A} ]\in [\mathbb {R} ]^{n\times m}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0fd9a7802bec756cf25e290e8d51c9d8c757b56c)
![{\displaystyle [\mathbf {b} ]\in [\mathbb {R} ]^{n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6759151da280e79f3bc9b0608bfd5009b666b475)
![{\displaystyle [\mathbf {x} ]\in [\mathbb {R} ]^{m}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a3c4763a20d2cb78d6d38ba20bb2d1e2416da7e8)


![{\displaystyle \mathbf {A} \in [\mathbf {A} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/20c6195d85a39ebfc0d8e1043eda9bac4c61e6c5)
![{\displaystyle \mathbf {b} \in [\mathbf {b} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/057e935649144aaec6d5cf58f2f384aaba05a560)


![{\displaystyle [\mathbf {A} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b49ad1a437f811c6dea6f5a1306c3e443b1b6ef4)
![{\displaystyle [\mathbf {b} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/8527cfd3a1b27a3761a39fceeb204d1bf640f5b6)
![{\displaystyle {\begin{pmatrix}{[a_{11}]}&\cdots &{[a_{1n}]}\\\vdots &\ddots &\vdots \\{[a_{n1}]}&\cdots &{[a_{nn}]}\end{pmatrix}}\cdot {\begin{pmatrix}{x_{1}}\\\vdots \\{x_{n}}\end{pmatrix}}={\begin{pmatrix}{[b_{1}]}\\\vdots \\{[b_{n}]}\end{pmatrix}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/74653a3f4b98c4aa7817f99be2b0ab744317ca5b)

![{\displaystyle 1/[a_{ii}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9a177c0f27440b1a1250863b6c1fedd5108875f9)
![{\displaystyle x_{j}\in [x_{j}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/12883b98919289aade5cadf2c7fe26628d32124e)
![{\displaystyle x_{j}\in {\frac {[b_{i}]-\sum \limits _{k\not =j}[a_{ik}]\cdot [x_{k}]}{[a_{ii}]}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/30d767c932c085c1b8805ab75909f123061b947f)
![{\displaystyle [x_{j}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9f3143be604648de9152dd93e3d409c9ff3a728d)
![{\displaystyle [x_{j}]\cap {\frac {[b_{i}]-\sum \limits _{k\not =j}[a_{ik}]\cdot [x_{k}]}{[a_{ii}]}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bddd27ea23b5dd444c2132924253489c52c465f9)
![{\displaystyle [\mathbf {A} ]\cdot \mathbf {x} =[\mathbf {b} ]{\mbox{,}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f79648fada1221bb03460b00ded658fd99462bd9)

![{\displaystyle (\mathbf {M} \cdot [\mathbf {A} ])\cdot \mathbf {x} =\mathbf {M} \cdot [\mathbf {b} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a95c32fdd88f4f3751eb859a0939ac4e6bfb578f)

![{\displaystyle \mathbf {M} \cdot [\mathbf {A} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/cbd3e24152064cc7686e0b589461941a4014f331)



![{\displaystyle \mathbf {z} \in [\mathbf {x} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3d05536f20e9c7373bd8ea13b5b8eb590f1d868b)
\cdot (\mathbf {z} -\mathbf {y} )}](http://wikimedia.org/api/rest_v1/media/math/render/svg/38870e9d970104f913495043e7dd7c50df424f88)


\cdot (\mathbf {z} -\mathbf {y} )=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/864212aaad5ccb1a97db4b0697509851f9e06624)
^{-1}\cdot f(\mathbf {y} )}](http://wikimedia.org/api/rest_v1/media/math/render/svg/66c26c14421ed860cf2d5330986f51620ba1332b)
^{-1}\cdot f(\mathbf {y} ))}](http://wikimedia.org/api/rest_v1/media/math/render/svg/cd0d1abcf312d4a861cd641b0611c9211e503427)
![{\displaystyle [\mathbf {x} ]\in [\mathbb {R} ]^{n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4f48b41921cf4ac1028e1f4b6a1cd424f7112b82)
![{\displaystyle [\mathbf {x} ]\cap \left(\mathbf {y} -[J_{f}](\mathbf {[x]} )^{-1}\cdot f(\mathbf {y} )\right)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/811b51184ab77e175110c3dca604a23bd717af03)

![{\displaystyle [x]=[-2,2]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a30331d65d35e6c55122b267178db7c1afa32a18)


![{\displaystyle [-2,2]\cap \left(0-{\frac {1}{2\cdot [-2,2]}}(0-2)\right)=[-2,2]\cap {\Big (}[{-\infty },{-0.5}]\cup [{0.5},{\infty }]{\Big )}=[{-2},{-0.5}]\cup [{0.5},{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/566fe56c844d8d2fbb33dadb0aea75df134aa22a)
![{\displaystyle x\in [{-2},{-0.5}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/99ca6eda43cbadbb65c2c95bf929e3b403178a97)
![{\displaystyle [{0.5},{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4ee9bc3d98165fb8bdf7c57bd29b9520ac45d40b)


![{\displaystyle g(x)=x^{2}-[2,3]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/695a37c43d1c8313a314f9f2689621ee0722b34a)
![{\displaystyle \left[-{\sqrt {3}},-{\sqrt {2}}\right]\cup \left[{\sqrt {2}},{\sqrt {3}}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/5417440767bf98c32b27e887a62b9f3dfc67ab6f)
![{\displaystyle [\mathbf {x} _{1}],\ldots ,[\mathbf {x} _{k}],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/538327562a1faec8c7e91bfa7705da0920a4de03)
![{\displaystyle [\mathbf {x} ]=\bigcup _{i=1}^{k}[\mathbf {x} _{i}],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3cf281da36a3c05ca33225499026f77fc1e32b5d)
![{\displaystyle f([\mathbf {x} ])=\bigcup _{i=1}^{k}f([\mathbf {x} _{i}]).}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f561c0b96273987d899af9fb2fca7e9b181ef94d)
\supseteq \bigcup _{i=1}^{k}[f]([\mathbf {x} _{i}]).}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ae9507525f6c188afb9ea8472380c29ee884f6ac)
}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2717077a8567f5422b647457dfbc437086e71181)
![{\displaystyle [x_{i1},x_{i2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/28fe01c53877dab323e3092dc3d145a35dc1f0cc)
![{\displaystyle [\mathbf {x} ]=([x_{11},x_{12}],\ldots ,[x_{n1},x_{n2}])}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2eaa75773cc7dc57642c627a28d380b65c76688d)
![{\displaystyle \left[x_{i1},{\tfrac {1}{2}}(x_{i1}+x_{i2})\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/75845cf5dbb00cb738216fa987cfc6205996eb1a)
![{\displaystyle \left[{\tfrac {1}{2}}(x_{i1}+x_{i2}),x_{i2}\right].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fb1faf5f9cdda3facf48392ad3ab41c1021876da)



![{\displaystyle \mathbf {p} \in [\mathbf {p} ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/49aa561cc72488b607c3fdf1e6f6a252da45ae69)
![{\displaystyle \{\mathbf {x} \,|\,\exists \mathbf {p} \in [\mathbf {p} ],f(\mathbf {x} ,\mathbf {p} )=0\}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/ca71015c6d47c7c3da1b6a17c2d75fdec0c59595)
![{\displaystyle x\in [x]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/171880f55704b7119665c4bf008a08c02f00e9da)
![{\displaystyle x\not \in [x]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/861a9d3eb363c42c1a42db4c37dcc983ef3ccd75)
![{\displaystyle \mu \in [0,1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/030ca0eebf53f89d13f475805d065c80355c9390)


![{\displaystyle \mu _{i}\in [0,1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/3d3f326c7768d7b92160ef76d925edd252c33b29)
![{\displaystyle \left[x^{(1)}\right]\supset \left[x^{(2)}\right]\supset \cdots \supset \left[x^{(k)}\right].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/45047c9b40d1ae4544d88a12838e008833fb534c)
![{\displaystyle \left[x^{(i)}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/a570fb736d5deff47052dc0ed38054cd81f4718c)



![{\displaystyle \left[x_{1}^{(1)}\right]\supset \cdots \supset \left[x_{1}^{(k)}\right],\ldots ,\left[x_{n}^{(1)}\right]\supset \cdots \supset \left[x_{n}^{(k)}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/aae168f056639f5bd2c99050e080dcf13d3bf1e1)
![{\displaystyle \left[y^{(1)}\right]\supset \cdots \supset \left[y^{(k)}\right],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/f547b2e02814ab784165fe59900169e2758b98e2)
![{\displaystyle \left[y^{(i)}\right]=f\left(\left[x_{1}^{(i)}\right],\ldots \left[x_{n}^{(i)}\right]\right)}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d44624dcc497f00d054f5f36cc2f894be102c30a)
![{\displaystyle \left[y^{(1)}\right]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/24652293bf2290386ca6256ebdb6399c49099a04)