Top Qs
Timeline
Chat
Perspective
Law of large numbers
Averages of repeated trials converge to the expected value From Wikipedia, the free encyclopedia
Remove ads
In probability theory, the law of large numbers is a mathematical law that states that the average of the results obtained from a large number of independent random samples converges to the true value, if it exists.[1] More formally, the law of large numbers states that given a sample of independent and identically distributed values, the sample mean converges to the true mean.
The law of large numbers is important because it guarantees stable long-term results for the averages of some random events.[1][2] For example, while a casino may lose money in a single spin of the roulette wheel, its earnings will tend towards a predictable percentage over a large number of spins. Any winning streak by a player will eventually be overcome by the parameters of the game. Importantly, the law applies (as the name indicates) only when a large number of observations are considered. There is no principle that a small number of observations will coincide with the expected value or that a streak of one value will immediately be "balanced" by the others (see the gambler's fallacy).
The law of large numbers only applies to the average of the results obtained from repeated trials and claims that this average converges to the expected value; it does not claim that the sum of n results gets close to the expected value times n as n increases.
Throughout its history, many mathematicians have refined this law. Today, the law of large numbers is used in many fields including statistics, probability theory, economics, and insurance.[3]
Remove ads
Examples
Summarize
Perspective
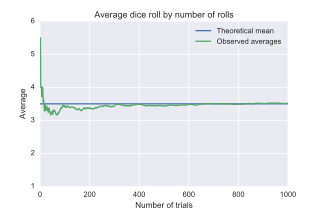
For example, a single roll of a six-sided dice produces one of the numbers 1, 2, 3, 4, 5, or 6, each with equal probability. Therefore, the expected value of the roll is:
According to the law of large numbers, if a large number of six-sided dice are rolled, the average of their values (sometimes called the sample mean) will approach 3.5, with the precision increasing as more dice are rolled.
It follows from the law of large numbers that the empirical probability of success in a series of Bernoulli trials will converge to the theoretical probability. For a Bernoulli random variable, the expected value is the theoretical probability of success, and the average of n such variables (assuming they are independent and identically distributed (i.i.d.)) is precisely the relative frequency.

For example, a fair coin toss is a Bernoulli trial. When a fair coin is flipped once, the theoretical probability that the outcome will be heads is equal to 1⁄2. Therefore, according to the law of large numbers, the proportion of heads in a "large" number of coin flips "should be" roughly 1⁄2. In particular, the proportion of heads after n flips will almost surely converge to 1⁄2 as n approaches infinity.
Although the proportion of heads (and tails) approaches 1⁄2, almost surely the absolute difference in the number of heads and tails will become large as the number of flips becomes large. That is, the probability that the absolute difference is a small number approaches zero as the number of flips becomes large. Also, almost surely the ratio of the absolute difference to the number of flips will approach zero. Intuitively, the expected difference grows, but at a slower rate than the number of flips.
Another good example of the law of large numbers is the Monte Carlo method. These methods are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The larger the number of repetitions, the better the approximation tends to be. The reason that this method is important is mainly that, sometimes, it is difficult or impossible to use other approaches.[4]
Remove ads
Limitation
The average of the results obtained from a large number of trials may fail to converge in some cases. For instance, the average of n results taken from the Cauchy distribution or some Pareto distributions (α<1) will not converge as n becomes larger; the reason is heavy tails.[5] The Cauchy distribution and the Pareto distribution represent two cases: the Cauchy distribution does not have an expectation,[6] whereas the expectation of the Pareto distribution (α<1) is infinite.[7] One way to generate the Cauchy-distributed example is where the random numbers equal the tangent of an angle uniformly distributed between −90° and +90°.[8] The median is zero, but the expected value does not exist, and indeed the average of n such variables have the same distribution as one such variable. It does not converge in probability toward zero (or any other value) as n goes to infinity.
If the trials embed a selection bias, typical in human economic/rational behaviour, the law of large numbers does not help in solving the bias, even if the number of trials is increased the selection bias remains.
Remove ads
History
Summarize
Perspective

- Top: With a single molecule, the motion appears to be quite random.
- Middle: With more molecules, there is clearly a trend where the solute fills the container more and more uniformly, but there are also random fluctuations.
- Bottom: With an enormous number of solute molecules (too many to see), the randomness is essentially gone: The solute appears to move smoothly and systematically from high-concentration areas to low-concentration areas. In realistic situations, chemists can describe diffusion as a deterministic macroscopic phenomenon (see Fick's laws), despite its underlying random nature.
The Italian mathematician Gerolamo Cardano (1501–1576) stated without proof that the accuracies of empirical statistics tend to improve with the number of trials.[9][3] This was then formalized as a law of large numbers. A special form of the law of large numbers (for a binary random variable) was first proved by Jacob Bernoulli.[10][3] It took him over 20 years to develop a sufficiently rigorous mathematical proof which was published in his Ars Conjectandi (The Art of Conjecturing) in 1713. He named this his "golden theorem" but it became generally known as "Bernoulli's theorem". This should not be confused with Bernoulli's principle, named after Jacob Bernoulli's nephew Daniel Bernoulli. In 1837, S. D. Poisson further described it under the name "la loi des grands nombres" ("the law of large numbers").[11][12][3] Thereafter, it was known under both names, but the "law of large numbers" is most frequently used.
After Bernoulli and Poisson published their efforts, other mathematicians also contributed to refinement of the law, including Chebyshev,[13] Markov, Borel, Cantelli, Kolmogorov and Khinchin.[3] Markov showed that the law can apply to a random variable that does not have a finite variance under some other weaker assumption, and Khinchin showed in 1929 that if the series consists of independent identically distributed random variables, it suffices that the expected value exists for the weak law of large numbers to be true.[14][15] These further studies have given rise to two prominent forms of the law of large numbers. One is called the "weak" law and the other the "strong" law, in reference to two different modes of convergence of the cumulative sample means to the expected value; in particular, as explained below, the strong form implies the weak.[14]
Remove ads
Forms
Summarize
Perspective
There are two different versions of the law of large numbers that are described below. They are called the strong law of large numbers and the weak law of large numbers.[16][1] Stated for the case where X1, X2, ... is an infinite sequence of independent and identically distributed (i.i.d.) Lebesgue integrable random variables with expected value E(X1) = E(X2) = ... = μ, both versions of the law state that the sample average
converges to the expected value:
| 1 |
(Lebesgue integrability of Xj means that the expected value E(Xj) exists according to Lebesgue integration and is finite. It does not mean that the associated probability measure is absolutely continuous with respect to Lebesgue measure.)
Introductory probability texts often additionally assume identical finite variance (for all ) and no correlation between random variables. In that case, the variance of the average of n random variables is
which can be used to shorten and simplify the proofs. This assumption of finite variance is not necessary. Large or infinite variance will make the convergence slower, but the law of large numbers holds anyway.[17]
Mutual independence of the random variables can be replaced by pairwise independence[18] or exchangeability[19] in both versions of the law.
The difference between the strong and the weak version is concerned with the mode of convergence being asserted. For interpretation of these modes, see Convergence of random variables.
Weak law
Simulation illustrating the law of large numbers. Each frame, a coin that is red on one side and blue on the other is flipped, and a dot is added in the corresponding column. A pie chart shows the proportion of red and blue so far. Notice that while the proportion varies significantly at first, it approaches 50% as the number of trials increases.
The weak law of large numbers (also called Khinchin's law) states that given a collection of independent and identically distributed (iid) samples from a random variable with finite mean, the sample mean converges in probability to the expected value[20]
| 2 |
That is, for any positive number ε,
Interpreting this result, the weak law states that for any nonzero margin specified (ε), no matter how small, with a sufficiently large sample there will be a very high probability that the average of the observations will be close to the expected value; that is, within the margin.
As mentioned earlier, the weak law applies in the case of i.i.d. random variables, but it also applies in some other cases. For example, the variance may be different for each random variable in the series, keeping the expected value constant. If the variances are bounded, then the law applies, as shown by Chebyshev as early as 1867. (If the expected values change during the series, then we can simply apply the law to the average deviation from the respective expected values. The law then states that this converges in probability to zero.) In fact, Chebyshev's proof works so long as the variance of the average of the first n values goes to zero as n goes to infinity.[15] As an example, assume that each random variable in the series follows a Gaussian distribution (normal distribution) with mean zero, but with variance equal to , which is not bounded. At each stage, the average will be normally distributed (as the average of a set of normally distributed variables). The variance of the sum is equal to the sum of the variances, which is asymptotic to . The variance of the average is therefore asymptotic to and goes to zero.
There are also examples of the weak law applying even though the expected value does not exist.
Strong law
The strong law of large numbers (also called Kolmogorov's law) states that the sample average converges almost surely to the expected value[21]
| 3 |
That is,
What this means is that, as the number of trials n goes to infinity, the probability that the average of the observations converges to the expected value, is equal to one. The modern proof of the strong law is more complex than that of the weak law, and relies on passing to an appropriate sub-sequence.[17]
The strong law of large numbers can itself be seen as a special case of the pointwise ergodic theorem. This view justifies the intuitive interpretation of the expected value (for Lebesgue integration only) of a random variable when sampled repeatedly as the "long-term average".
Law 3 is called the strong law because random variables which converge strongly (almost surely) are guaranteed to converge weakly (in probability). However the weak law is known to hold in certain conditions where the strong law does not hold and then the convergence is only weak (in probability). See Differences between the weak law and the strong law.
The strong law applies to independent identically distributed random variables having an expected value (like the weak law). This was proved by Kolmogorov in 1930. It can also apply in other cases. Kolmogorov also showed, in 1933, that if the variables are independent and identically distributed, then for the average to converge almost surely on something (this can be considered another statement of the strong law), it is necessary that they have an expected value (and then of course the average will converge almost surely on that).[22]
If the summands are independent but not identically distributed, then
| 2 |
provided that each Xk has a finite second moment and
This statement is known as Kolmogorov's strong law, see e.g. Sen & Singer (1993, Theorem 2.3.10).
Differences between the weak law and the strong law
The weak law states that for a specified large n, the average is likely to be near μ.[23] Thus, it leaves open the possibility that happens an infinite number of times, although at infrequent intervals. (Not necessarily for all n).
The strong law shows that this almost surely will not occur. I.e., with probability 1 for any ε > 0 the inequality holds for all large enough n.[24]
The strong law does not hold in the following cases, but the weak law does.[25][26]
- Let X be an exponentially distributed random variable with parameter 1. The random variable has no expected value according to Lebesgue integration, but using conditional convergence and interpreting the integral as a Dirichlet integral, which is an improper Riemann integral, we can say:
- Let X be a geometrically distributed random variable with probability 0.5. The random variable does not have an expected value in the conventional sense because the infinite series is not absolutely convergent, but using conditional convergence, we can say:
- If the cumulative distribution function of a random variable is then it has no expected value, but the weak law is true.[27][28]
- Let Xk be plus or minus (starting at sufficiently large k so that the denominator is positive) with probability 1⁄2 for each.[22] The variance of Xk is then Kolmogorov's strong law does not apply because the partial sum in his criterion up to k = n is asymptotic to and this is unbounded. If we replace the random variables with Gaussian variables having the same variances, namely , then the average at any point will also be normally distributed. The width of the distribution of the average will tend toward zero (standard deviation asymptotic to ), but for a given ε, there is probability which does not go to zero with n, while the average sometime after the nth trial will come back up to ε. Since the width of the distribution of the average is not zero, it must have a positive lower bound p(ε), which means there is a probability of at least p(ε) that the average will attain ε after n trials. It will happen with probability p(ε)/2 before some m which depends on n. But even after m, there is still a probability of at least p(ε) that it will happen. (This seems to indicate that p(ε)=1 and the average will attain ε an infinite number of times.)
Uniform laws of large numbers
There are extensions of the law of large numbers to collections of estimators, where the convergence is uniform over the collection; thus the name uniform law of large numbers.
Suppose f(x,θ) is some function defined for θ ∈ Θ, and continuous in θ. Then for any fixed θ, the sequence {f(X1,θ), f(X2,θ), ...} will be a sequence of independent and identically distributed random variables, such that the sample mean of this sequence converges in probability to E[f(X,θ)]. This is the pointwise (in θ) convergence.
A particular example of a uniform law of large numbers states the conditions under which the convergence happens uniformly in θ. If[29][30]
- Θ is compact,
- f(x,θ) is continuous at each θ ∈ Θ for almost all xs, and measurable function of x at each θ.
- there exists a dominating function d(x) such that E[d(X)] < ∞, and
Then E[f(X,θ)] is continuous in θ, and
This result is useful to derive consistency of a large class of estimators (see Extremum estimator).
Borel's law of large numbers
Borel's law of large numbers, named after Émile Borel, states that if an experiment is repeated a large number of times, independently under identical conditions, then the proportion of times that any specified event is expected to occur approximately equals the probability of the event's occurrence on any particular trial; the larger the number of repetitions, the better the approximation tends to be. More precisely, if E denotes the event in question, p its probability of occurrence, and Nn(E) the number of times E occurs in the first n trials, then with probability one,[31]
This theorem makes rigorous the intuitive notion of probability as the expected long-run relative frequency of an event's occurrence. It is a special case of any of several more general laws of large numbers in probability theory.
Remove ads
Proof of the weak law
Summarize
Perspective
Given X1, X2, ... an infinite sequence of i.i.d. random variables with finite expected value , we are interested in the convergence of the sample average
The weak law of large numbers states:
| 2 |
Proof using Chebyshev's inequality assuming finite variance
This proof uses the assumption of finite variance (for all ). The independence of the random variables implies no correlation between them, and we have that
The common mean μ of the sequence is the mean of the sample average:
Using Chebyshev's inequality on results in
This may be used to obtain the following:
As n approaches infinity, the expression approaches 1. And by definition of convergence in probability, we have obtained
| 2 |
Proof using convergence of characteristic functions
By Taylor's theorem for complex functions, the characteristic function of any random variable, X, with finite mean μ, can be written as
All X1, X2, ... have the same characteristic function, so we will simply denote this φX.
Among the basic properties of characteristic functions there are
if X and Y are independent.
These rules can be used to calculate the characteristic function of in terms of φX:
The limit eitμ is the characteristic function of the constant random variable μ, and hence by the Lévy continuity theorem, converges in distribution to μ:
μ is a constant, which implies that convergence in distribution to μ and convergence in probability to μ are equivalent (see Convergence of random variables.) Therefore,
| 2 |
This shows that the sample mean converges in probability to the derivative of the characteristic function at the origin, as long as the latter exists.
Remove ads
Proof of the strong law
We give a relatively simple proof of the strong law under the assumptions that the are iid, , , and .
Let us first note that without loss of generality we can assume that by centering. In this case, the strong law says that
or It is equivalent to show that Note that and thus to prove the strong law we need to show that for every , we have Define the events , and if we can show that then the Borel-Cantelli Lemma implies the result. So let us estimate .
We compute We first claim that every term of the form where all subscripts are distinct, must have zero expectation. This is because by independence, and the last term is zero—and similarly for the other terms. Therefore the only terms in the sum with nonzero expectation are and . Since the are identically distributed, all of these are the same, and moreover .
There are terms of the form and terms of the form , and so Note that the right-hand side is a quadratic polynomial in , and as such there exists a such that for sufficiently large. By Markov, for sufficiently large, and therefore this series is summable. Since this holds for any , we have established the strong law of large numbers.[32] The proof can be strengthened immensely by dropping all finiteness assumptions on the second and fourth moments. It can also be extended for example to discuss partial sums of distributions without any finite moments. Such proofs use more intricate arguments to prove the same Borel-Cantelli predicate, a strategy attributed to Kolmogorov to conceptually bring the limit inside the probability parentheses. [33]
Remove ads
Consequences
Summarize
Perspective
The law of large numbers provides an expectation of an unknown distribution from a realization of the sequence, but also any feature of the probability distribution.[1] By applying Borel's law of large numbers, one could easily obtain the probability mass function. For each event in the objective probability mass function, one could approximate the probability of the event's occurrence with the proportion of times that any specified event occurs. The larger the number of repetitions, the better the approximation. As for the continuous case: , for small positive h. Thus, for large n:
With this method, one can cover the whole x-axis with a grid (with grid size 2h) and obtain a bar graph which is called a histogram.
Remove ads
Applications
Summarize
Perspective
One application of the law of large numbers is an important method of approximation known as the Monte Carlo method,[3] which uses a random sampling of numbers to approximate numerical results. The algorithm to compute an integral of f(x) on an interval [a, b] is as follows:[3]
- Simulate uniform random variables X1, X2, …, Xn which can be done using a software, and use a random number table that gives U1, U2, …, Un independent and identically distributed (i.i.d.) random variables on [0, 1]. Then let Xi = a + (b - a) Ui for i= 1, 2, …, n. Then X1, X2, …, Xn are independent and identically distributed uniform random variables on [a, b].
- Evaluate f(X1), f(X2), …, f(Xn).
- Take the average of f(X1), f(X2), …, f(Xn) by computing , and then by the strong law of large numbers this converges to .
We can find the integral of on [-1, 2]. Using traditional methods to compute this integral is very difficult, so the Monte Carlo method can be used here.[3] Using the above algorithm, we get
when n = 25
and
when n = 250.
We observe that as n increases, the numerical value also increases. When we get the actual results for the integral we get
.
When the LLN was used, the approximation of the integral was closer to its true value, and thus more accurate.[3]
Another example is the integration of over [0, 1].[34] Using the Monte Carlo method and the LLN, we can see that as the number of samples increases, the numerical value gets ever closer to 0.4180233.[34]
Remove ads
See also
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads














![{\displaystyle {\overline {X}}_{n}-\operatorname {E} {\big [}{\overline {X}}_{n}{\big ]}\ {\overset {\text{a.s.}}{\longrightarrow }}\ 0,}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4d78fdcd0502a7beb22812467a91e5e8eb6acc95)
![{\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k^{2}}}\operatorname {Var} [X_{k}]<\infty .}](http://wikimedia.org/api/rest_v1/media/math/render/svg/849940f493b14c4f019c225b494d3afcc1b6ca29)














![{\displaystyle \sup _{\theta \in \Theta }\left\|{\frac {1}{n}}\sum _{i=1}^{n}f(X_{i},\theta )-\operatorname {E} [f(X,\theta )]\right\|{\overset {\mathrm {P} }{\rightarrow }}\ 0.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bb54a1fa254d7f7ed846e6cabc7a8a1f789a92aa)








![{\displaystyle \varphi _{{\overline {X}}_{n}}(t)=\left[\varphi _{X}\left({t \over n}\right)\right]^{n}=\left[1+i\mu {t \over n}+o\left({t \over n}\right)\right]^{n}\,\rightarrow \,e^{it\mu },\quad {\text{as}}\quad n\to \infty .}](http://wikimedia.org/api/rest_v1/media/math/render/svg/244552d66f95379a21ce004941baeb45f7cccc1d)


![{\displaystyle {\mathbb {E} }[X_{i}]=:\mu <\infty }](http://wikimedia.org/api/rest_v1/media/math/render/svg/945172be4f9585c1118ce2188617324caa19fdcd)

![{\displaystyle {\mathbb {E} }[X_{i}^{4}]=:\tau <\infty }](http://wikimedia.org/api/rest_v1/media/math/render/svg/089cf58c0dc1335eb8078f5ea60b0f37e6ba7080)










![{\displaystyle {\mathbb {E} }[S_{n}^{4}]={\mathbb {E} }\left[\left(\sum _{i=1}^{n}X_{i}\right)^{4}\right]={\mathbb {E} }\left[\sum _{1\leq i,j,k,l\leq n}X_{i}X_{j}X_{k}X_{l}\right].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1fed903db3f4b0526dcf5ee44a967bac45eeb9ef)

![{\displaystyle {\mathbb {E} }[X_{i}^{3}X_{j}]={\mathbb {E} }[X_{i}^{3}]{\mathbb {E} }[X_{j}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/45c42392e59a0113c14527a2256b4d2c6864c7ad)
![{\displaystyle {\mathbb {E} }[X_{i}^{4}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d33c75b5a66fea493222d077bb54d98f960bf082)
![{\displaystyle {\mathbb {E} }[X_{i}^{2}X_{j}^{2}]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d22184db5e10e679e4d366aac99b4ca70205d99f)
![{\displaystyle {\mathbb {E} }[X_{i}^{2}X_{j}^{2}]=({\mathbb {E} }[X_{i}^{2}])^{2}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2296e8ef46d13f64a00609c21c838e842d739a69)


![{\displaystyle ({\mathbb {E} }[X_{i}^{2}])^{2}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/95021f2378d75a081aae6398232a2ac38ae0f7a5)
![{\displaystyle {\mathbb {E} }[S_{n}^{4}]=n\tau +3n(n-1)\sigma ^{4}.}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0800261defee5ae3d5e94f20fc83fe231a277fee)

![{\displaystyle {\mathbb {E} }[S_{n}^{4}]\leq Cn^{2}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/93c1f1e646da5df999c4c952025d757291bd2f0b)
![{\displaystyle \Pr(|S_{n}|\geq n\epsilon )\leq {\frac {1}{(n\epsilon )^{4}}}{\mathbb {E} }[S_{n}^{4}]\leq {\frac {C}{\epsilon ^{4}n^{2}}},}](http://wikimedia.org/api/rest_v1/media/math/render/svg/bb57fec48553c08499aded735ca22333704137f2)
![{\displaystyle C=(a-h,a+h]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/fb64a0e36558e4189ac0f21fef2370c4649aa542)







