Top Qs
Timeline
Chat
Perspective
Partial derivative
Derivative of a function with multiple variables From Wikipedia, the free encyclopedia
Remove ads
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry.
The partial derivative of a function with respect to the variable is variously denoted by
, , , , , , or .
It can be thought of as the rate of change of the function in the -direction.
Sometimes, for , the partial derivative of with respect to is denoted as Since a partial derivative generally has the same arguments as the original function, its functional dependence is sometimes explicitly signified by the notation, such as in:
The symbol used to denote partial derivatives is ∂. One of the first known uses of this symbol in mathematics is by Marquis de Condorcet from 1770,[1] who used it for partial differences. The modern partial derivative notation was created by Adrien-Marie Legendre (1786), although he later abandoned it; Carl Gustav Jacob Jacobi reintroduced the symbol in 1841.[2]
Remove ads
Definition
Like ordinary derivatives, the partial derivative is defined as a limit. Let U be an open subset of and a function. The partial derivative of f at the point with respect to the i-th variable xi is defined as
Where is the unit vector of i-th variable xi. Even if all partial derivatives exist at a given point a, the function need not be continuous there. However, if all partial derivatives exist in a neighborhood of a and are continuous there, then f is totally differentiable in that neighborhood and the total derivative is continuous. In this case, it is said that f is a C1 function. This can be used to generalize for vector valued functions, , by carefully using a componentwise argument.
The partial derivative can be seen as another function defined on U and can again be partially differentiated. If the direction of derivative is not repeated, it is called a mixed partial derivative. If all mixed second order partial derivatives are continuous at a point (or on a set), f is termed a C2 function at that point (or on that set); in this case, the partial derivatives can be exchanged by Clairaut's theorem:
Remove ads
Notation
Summarize
Perspective
For the following examples, let f be a function in x, y, and z.
First-order partial derivatives:
Second-order partial derivatives:
Second-order mixed derivatives:
Higher-order partial and mixed derivatives:
When dealing with functions of multiple variables, some of these variables may be related to each other, thus it may be necessary to specify explicitly which variables are being held constant to avoid ambiguity. In fields such as statistical mechanics, the partial derivative of f with respect to x, holding y and z constant, is often expressed as
Conventionally, for clarity and simplicity of notation, the partial derivative function and the value of the function at a specific point are conflated by including the function arguments when the partial derivative symbol (Leibniz notation) is used. Thus, an expression like
is used for the function, while
might be used for the value of the function at the point . However, this convention breaks down when we want to evaluate the partial derivative at a point like . In such a case, evaluation of the function must be expressed in an unwieldy manner as
or
in order to use the Leibniz notation. Thus, in these cases, it may be preferable to use the Euler differential operator notation with as the partial derivative symbol with respect to the i-th variable. For instance, one would write for the example described above, while the expression represents the partial derivative function with respect to the first variable.[3]
For higher order partial derivatives, the partial derivative (function) of with respect to the j-th variable is denoted . That is, , so that the variables are listed in the order in which the derivatives are taken, and thus, in reverse order of how the composition of operators is usually notated. Of course, Clairaut's theorem implies that as long as comparatively mild regularity conditions on f are satisfied.
Remove ads
Gradient
Summarize
Perspective
An important example of a function of several variables is the case of a scalar-valued function on a domain in Euclidean space (e.g., on or ). In this case f has a partial derivative with respect to each variable xj. At the point a, these partial derivatives define the vector
This vector is called the gradient of f at a. If f is differentiable at every point in some domain, then the gradient is a vector-valued function ∇f which takes the point a to the vector ∇f(a). Consequently, the gradient produces a vector field.
A common abuse of notation is to define the del operator (∇) as follows in three-dimensional Euclidean space with unit vectors :
Or, more generally, for n-dimensional Euclidean space with coordinates and unit vectors :
Remove ads
Directional derivative
Summarize
Perspective

The directional derivative of a scalar function along a vector is the function defined by the limit[4]
This definition is valid in a broad range of contexts, for example, where the norm of a vector (and hence a unit vector) is defined.[5]
Remove ads
Example
Summarize
Perspective
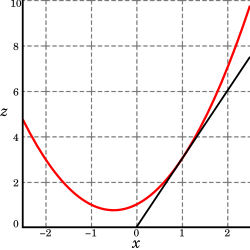
Suppose that f is a function of more than one variable. For instance,
A graph of z = x2 + xy + y2. For the partial derivative at (1, 1) that leaves y constant, the corresponding tangent line is parallel to the xz-plane.
The graph of this function defines a surface in Euclidean space. To every point on this surface, there are an infinite number of tangent lines. Partial differentiation is the act of choosing one of these lines and finding its slope. Usually, the lines of most interest are those that are parallel to the xz-plane, and those that are parallel to the yz-plane (which result from holding either y or x constant, respectively).
To find the slope of the line tangent to the function at P(1, 1) and parallel to the xz-plane, we treat y as a constant. The graph and this plane are shown on the right. Below, we see how the function looks on the plane y = 1. By finding the derivative of the equation while assuming that y is a constant, we find that the slope of f at the point (x, y) is:
So at (1, 1), by substitution, the slope is 3. Therefore,
at the point (1, 1). That is, the partial derivative of z with respect to x at (1, 1) is 3, as shown in the graph.
The function f can be reinterpreted as a family of functions of one variable indexed by the other variables:
In other words, every value of y defines a function, denoted fy, which is a function of one variable x.[6] That is,
In this section the subscript notation fy denotes a function contingent on a fixed value of y, and not a partial derivative.
Once a value of y is chosen, say a, then f(x,y) determines a function fa which traces a curve x2 + ax + a2 on the xz-plane:
In this expression, a is a constant, not a variable, so fa is a function of only one real variable, that being x. Consequently, the definition of the derivative for a function of one variable applies:
The above procedure can be performed for any choice of a. Assembling the derivatives together into a function gives a function which describes the variation of f in the x direction:
This is the partial derivative of f with respect to x. Here '∂' is a rounded 'd' called the partial derivative symbol; to distinguish it from the letter 'd', '∂' is sometimes pronounced "partial".
Remove ads
Higher order partial derivatives
Summarize
Perspective
Second and higher order partial derivatives are defined analogously to the higher order derivatives of univariate functions. For the function the "own" second partial derivative with respect to x is simply the partial derivative of the partial derivative (both with respect to x):[7]: 316–318
The cross partial derivative with respect to x and y is obtained by taking the partial derivative of f with respect to x, and then taking the partial derivative of the result with respect to y, to obtain
Schwarz's theorem states that if the second derivatives are continuous, the expression for the cross partial derivative is unaffected by which variable the partial derivative is taken with respect to first and which is taken second. That is,
or equivalently
Own and cross partial derivatives appear in the Hessian matrix which is used in the second order conditions in optimization problems. The higher order partial derivatives can be obtained by successive differentiation
Remove ads
Antiderivative analogue
Summarize
Perspective
There is a concept for partial derivatives that is analogous to antiderivatives for regular derivatives. Given a partial derivative, it allows for the partial recovery of the original function.
Consider the example of
The so-called partial integral can be taken with respect to x (treating y as constant, in a similar manner to partial differentiation):
Here, the constant of integration is no longer a constant, but instead a function of all the variables of the original function except x. The reason for this is that all the other variables are treated as constant when taking the partial derivative, so any function which does not involve x will disappear when taking the partial derivative, and we have to account for this when we take the antiderivative. The most general way to represent this is to have the constant represent an unknown function of all the other variables.
Thus the set of functions , where g is any one-argument function, represents the entire set of functions in variables x, y that could have produced the x-partial derivative .
If all the partial derivatives of a function are known (for example, with the gradient), then the antiderivatives can be matched via the above process to reconstruct the original function up to a constant. Unlike in the single-variable case, however, not every set of functions can be the set of all (first) partial derivatives of a single function. In other words, not every vector field is conservative.
Remove ads
Applications
Summarize
Perspective
Geometry
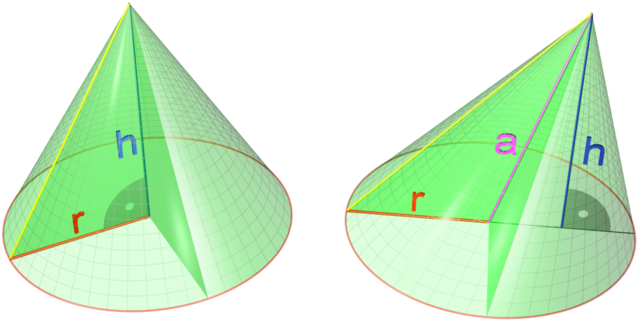
The volume V of a cone depends on the cone's height h and its radius r according to the formula
The partial derivative of V with respect to r is
which represents the rate with which a cone's volume changes if its radius is varied and its height is kept constant. The partial derivative with respect to h equals , which represents the rate with which the volume changes if its height is varied and its radius is kept constant.
By contrast, the total derivative of V with respect to r and h are respectively
The difference between the total and partial derivative is the elimination of indirect dependencies between variables in partial derivatives.
If (for some arbitrary reason) the cone's proportions have to stay the same, and the height and radius are in a fixed ratio k,
This gives the total derivative with respect to r,
which simplifies to
Similarly, the total derivative with respect to h is
The total derivative with respect to both r and h of the volume intended as scalar function of these two variables is given by the gradient vector
Optimization
Partial derivatives appear in any calculus-based optimization problem with more than one choice variable. For example, in economics a firm may wish to maximize profit π(x, y) with respect to the choice of the quantities x and y of two different types of output. The first order conditions for this optimization are πx = 0 = πy. Since both partial derivatives πx and πy will generally themselves be functions of both arguments x and y, these two first order conditions form a system of two equations in two unknowns.
Thermodynamics, quantum mechanics and mathematical physics
Partial derivatives appear in thermodynamic equations like Gibbs-Duhem equation, in quantum mechanics as in Schrödinger wave equation, as well as in other equations from mathematical physics. The variables being held constant in partial derivatives here can be ratios of simple variables like mole fractions xi in the following example involving the Gibbs energies in a ternary mixture system:
Express mole fractions of a component as functions of other components' mole fraction and binary mole ratios:
Differential quotients can be formed at constant ratios like those above:
Ratios X, Y, Z of mole fractions can be written for ternary and multicomponent systems:
which can be used for solving partial differential equations like:
This equality can be rearranged to have differential quotient of mole fractions on one side.
Image resizing
Partial derivatives are key to target-aware image resizing algorithms. Widely known as seam carving, these algorithms require each pixel in an image to be assigned a numerical 'energy' to describe their dissimilarity against orthogonal adjacent pixels. The algorithm then progressively removes rows or columns with the lowest energy. The formula established to determine a pixel's energy (magnitude of gradient at a pixel) depends heavily on the constructs of partial derivatives.
Economics
Partial derivatives play a prominent role in economics, in which most functions describing economic behaviour posit that the behaviour depends on more than one variable. For example, a societal consumption function may describe the amount spent on consumer goods as depending on both income and wealth; the marginal propensity to consume is then the partial derivative of the consumption function with respect to income.
Remove ads
See also
Notes
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads













































![{\displaystyle \nabla =\left[{\frac {\partial }{\partial x}}\right]{\hat {\mathbf {i} }}+\left[{\frac {\partial }{\partial y}}\right]{\hat {\mathbf {j} }}+\left[{\frac {\partial }{\partial z}}\right]{\hat {\mathbf {k} }}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/b7c70b5bce4676294a2be68361d333b3f44ce478)


![{\displaystyle \nabla =\sum _{j=1}^{n}\left[{\frac {\partial }{\partial x_{j}}}\right]{\hat {\mathbf {e} }}_{j}=\left[{\frac {\partial }{\partial x_{1}}}\right]{\hat {\mathbf {e} }}_{1}+\left[{\frac {\partial }{\partial x_{2}}}\right]{\hat {\mathbf {e} }}_{2}+\dots +\left[{\frac {\partial }{\partial x_{n}}}\right]{\hat {\mathbf {e} }}_{n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4449e767ec489248b3a285415bf722bd550932c7)