Top Qs
Timeline
Chat
Perspective
Pythagorean theorem
Relation between sides of a right triangle From Wikipedia, the free encyclopedia
Remove ads
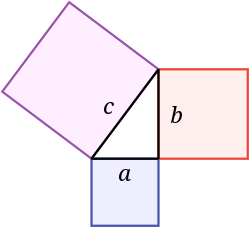
In mathematics, the Pythagorean theorem or Pythagoras's theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides.[1]
The theorem can be written as an equation relating the lengths of the sides a, b and the hypotenuse c, sometimes called the Pythagorean equation:[2] The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years.
When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared distance between two points equals the sum of squares of the difference in each coordinate between the points.
The theorem can be generalized in various ways: to higher-dimensional spaces, to spaces that are not Euclidean, to objects that are not right triangles, and to objects that are not triangles at all but n-dimensional solids.
Remove ads
Proofs using constructed squares
Summarize
Perspective

(The area of the white space remains constant throughout the translation rearrangement of the triangles. At all moments in time, the area is always c2. And likewise, at all moments in time, the area is always a2 + b2.)
Rearrangement proofs
In one rearrangement proof, two squares are used whose sides have a measure of and which contain four right triangles whose sides are a, b and c, with the hypotenuse being c. In the square on the right side, the triangles are placed such that the corners of the square correspond to the corners of the right angle in the triangles, forming a square in the center whose sides are length c. Each outer square has an area of (a + b)2 as well as 2ab + c2, with 2ab representing the total area of the four triangles. Within the big square on the left side, the four triangles are moved to form two similar rectangles with sides of length a and b. These rectangles in their new position have now delineated two new squares, one having side length a is formed in the bottom-left corner, and another square of side length b formed in the top-right corner. In this new position, this left side now has a square of area (a + b)2 as well as 2ab + a2 + b2. Since both squares have the area of (a + b)2 it follows that the other measure of the square area also equal each other such that 2ab + c2 = ab + a2 + b2. With the area of the four triangles removed from both side of the equation what remains is a2 + b2 = c2.[3]
In another proof rectangles in the second box can also be placed such that both have one corner that correspond to consecutive corners of the square. In this way they also form two boxes, this time in consecutive corners, with areas a2 and b2 which will again lead to a second square of with the area 2ab + a2 + b2.
English mathematician Sir Thomas Heath gives this proof in his commentary on Proposition I.47 in Euclid's Elements, and mentions the proposals of German mathematicians Carl Anton Bretschneider and Hermann Hankel that Pythagoras may have known this proof. Heath himself favors a different proposal for a Pythagorean proof, but acknowledges from the outset of his discussion "that the Greek literature which we possess belonging to the first five centuries after Pythagoras contains no statement specifying this or any other particular great geometric discovery to him."[4] Recent scholarship has cast increasing doubt on any sort of role for Pythagoras as a creator of mathematics, although debate about this continues.[5]
Algebraic proofs

The theorem can be proved algebraically using four copies of the same triangle arranged symmetrically around a square with side c, as shown in the lower part of the diagram.[6] This results in a larger square, with side a + b and area (a + b)2. The four triangles and the square side c must have the same area as the larger square, giving
A similar proof uses four copies of a right triangle with sides a, b and c, arranged inside a square with side c as in the top half of the diagram.[7] The triangles are similar with area 1/2ab, while the small square has side b − a and area (b − a)2. The area of the large square is therefore
But this is a square with side c and area c2, so
Remove ads
Other proofs of the theorem
Summarize
Perspective
This theorem may have more known proofs than any other (the law of quadratic reciprocity being another contender for that distinction); the book The Pythagorean Proposition contains 370 proofs.[8]
Proof using similar triangles

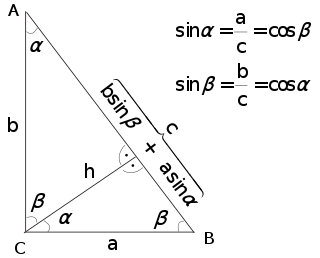
This proof is based on the proportionality of the sides of three similar triangles, that is, upon the fact that the ratio of any two corresponding sides of similar triangles is the same regardless of the size of the triangles.
Let ABC represent a right triangle, with the right angle located at C, as shown on the figure. Draw the altitude from point C, and call H its intersection with the side AB. Point H divides the length of the hypotenuse c into parts d and e. The new triangle, ACH, is similar to triangle ABC, because they both have a right angle (by definition of the altitude), and they share the angle at A, meaning that the third angle will be the same in both triangles as well, marked as θ in the figure. By a similar reasoning, the triangle CBH is also similar to ABC. The proof of similarity of the triangles requires the triangle postulate: The sum of the angles in a triangle is two right angles, and is equivalent to the parallel postulate. Similarity of the triangles leads to the equality of ratios of corresponding sides:
The first result equates the cosines of the angles θ, whereas the second result equates their sines.
These ratios can be written as Summing these two equalities results in which, after simplification, demonstrates the Pythagorean theorem:
The role of this proof in history is the subject of much speculation. The underlying question is why Euclid did not use this proof, but invented another. One conjecture is that the proof by similar triangles involved a theory of proportions, a topic not discussed until later in the Elements, and that the theory of proportions needed further development at that time.[9]
Einstein's proof by dissection without rearrangement
Albert Einstein gave a proof by dissection in which the pieces do not need to be moved.[10] Instead of using a square on the hypotenuse and two squares on the legs, one can use any other shape that includes the hypotenuse, and two similar shapes that each include one of two legs instead of the hypotenuse (see Similar figures on the three sides). In Einstein's proof, the shape that includes the hypotenuse is the right triangle itself. The dissection consists of dropping a perpendicular from the vertex of the right angle of the triangle to the hypotenuse, thus splitting the whole triangle into two parts. Those two parts have the same shape as the original right triangle,and have the legs of the original triangle as their hypotenuses, and the sum of their areas is that of the original triangle. Because the ratio of the area of a right triangle to the square of its hypotenuse is the same for similar triangles, the relationship between the areas of the three triangles holds for the squares of the sides of the large triangle as well.
Euclid's proof

In outline, here is how the proof in Euclid's Elements proceeds. The large square is divided into a left and right rectangle. A triangle is constructed that has half the area of the left rectangle. Then another triangle is constructed that has half the area of the square on the left-most side. These two triangles are shown to be congruent, proving this square has the same area as the left rectangle. This argument is followed by a similar version for the right rectangle and the remaining square. Putting the two rectangles together to reform the square on the hypotenuse, its area is the same as the sum of the area of the other two squares. The details follow.
Let A, B, C be the vertices of a right triangle, with a right angle at A. Drop a perpendicular from A to the side opposite the hypotenuse in the square on the hypotenuse. That line divides the square on the hypotenuse into two rectangles, each having the same area as one of the two squares on the legs.
For the formal proof, we require four elementary lemmata:
- If two triangles have two sides of the one equal to two sides of the other, each to each, and the angles included by those sides equal, then the triangles are congruent (side-angle-side).
- The area of a triangle is half the area of any parallelogram on the same base and having the same altitude.
- The area of a rectangle is equal to the product of two adjacent sides.
- The area of a square is equal to the product of two of its sides (follows from 3).
Next, each top square is related to a triangle congruent with another triangle related in turn to one of two rectangles making up the lower square.[11]


The proof is as follows:
- Let ACB be a right-angled triangle with right angle CAB.
- On each of the sides BC, AB, and CA, squares are drawn, CBDE, BAGF, and ACIH, in that order. The construction of squares requires the immediately preceding theorems in Euclid, and depends upon the parallel postulate.[12]
- From A, draw a line parallel to BD and CE. It will perpendicularly intersect BC and DE at K and L, respectively.
- Join CF and AD, to form the triangles BCF and BDA.
- Angles CAB and BAG are both right angles; therefore C, A, and G are collinear.
- Angles CBD and FBA are both right angles; therefore angle ABD equals angle FBC, since both are the sum of a right angle and angle ABC.
- Since AB is equal to FB, BD is equal to BC and angle ABD equals angle FBC, triangle ABD must be congruent to triangle FBC.
- Since A-K-L is a straight line, parallel to BD, then rectangle BDLK has twice the area of triangle ABD because they share the base BD and have the same altitude BK, i.e., a line normal to their common base, connecting the parallel lines BD and AL. (lemma 2)
- Since C is collinear with A and G, and this line is parallel to FB, then square BAGF must be twice in area to triangle FBC.
- Therefore, rectangle BDLK must have the same area as square BAGF = AB2.
- By applying steps 3 to 10 to the other side of the figure, it can be similarly shown that rectangle CKLE must have the same area as square ACIH = AC2.
- Adding these two results, AB2 + AC2 = BD × BK + KL × KC
- Since BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
- Therefore, AB2 + AC2 = BC2, since CBDE is a square (BD × BC = BC2).
This proof, which appears in Euclid's Elements as that of Proposition 47 in Book 1, demonstrates that the area of the square on the hypotenuse is the sum of the areas of the other two squares.[13][14] This is quite distinct from the proof by similarity of triangles, which is conjectured to be the proof that Pythagoras used.[15][a]
Proofs by dissection and rearrangement
Another by rearrangement is given by the middle animation. A large square is formed with area c2, from four identical right triangles with sides a, b and c, fitted around a small central square. Then two rectangles are formed with sides a and b by moving the triangles. Combining the smaller square with these rectangles produces two squares of areas a2 and b2, which must have the same area as the initial large square.[16]
The third, rightmost image also gives a proof. The upper two squares are divided as shown by the blue and green shading, into pieces that when rearranged can be made to fit in the lower square on the hypotenuse – or conversely the large square can be divided as shown into pieces that fill the other two. This way of cutting one figure into pieces and rearranging them to get another figure is called dissection. This shows the area of the large square equals that of the two smaller ones.[17]
 |
 |
 |
Proof by area-preserving shearing

As shown in the accompanying animation, area-preserving shear mappings and translations can transform the squares on the sides adjacent to the right-angle onto the square on the hypotenuse, together covering it exactly.[18] Each shear leaves the base and height unchanged, thus leaving the area unchanged too. The translations also leave the area unchanged, as they do not alter the shapes at all. Each square is first sheared into a parallelogram, and then into a rectangle which can be translated onto one section of the square on the hypotenuse.
Other algebraic proofs
A related proof by U.S. president James A. Garfield was published before he was elected president; while he was a U.S. representative.[19][20][21] Instead of a square it uses a trapezoid, which can be constructed from the square in the second of the above proofs by bisecting along a diagonal of the inner square, to give the trapezoid as shown in the diagram. The area of the trapezoid can be calculated to be half the area of the square, that is
The inner square is similarly halved, and there are only two triangles so the proof proceeds as above except for a factor of , which is removed by multiplying by two to give the result.
Proof using differentials
One can arrive at the Pythagorean theorem by studying how changes in a side produce a change in the hypotenuse and employing calculus.[22][23][24]
The triangle ABC is a right triangle, as shown in the upper part of the diagram, with BC the hypotenuse. At the same time the triangle lengths are measured as shown, with the hypotenuse of length y, the side AC of length x and the side AB of length a, as seen in the lower diagram part.
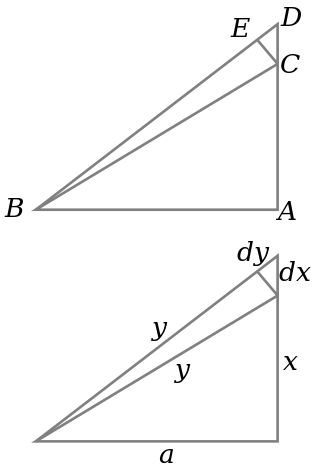
If x is increased by a small amount dx by extending the side AC slightly to D, then y also increases by dy. These form two sides of a triangle, CDE, which (with E chosen so CE is perpendicular to the hypotenuse) is a right triangle approximately similar to ABC. Therefore, the ratios of their sides must be the same, that is: This can be rewritten as y dy = x dx, which is a differential equation that can be solved by direct integration: giving The constant can be deduced from x = 0, y = a to give the equation This is more of an intuitive proof than a formal one: it can be made more rigorous if proper limits are used in place of dx and dy.
Remove ads
Converse
Summarize
Perspective
The converse of the theorem is also true:[25]
Given a triangle with sides of length a, b, and c, if a2 + b2 = c2, then the angle between sides a and b is a right angle.
For any three positive real numbers a, b, and c such that a2 + b2 = c2, there exists a triangle with sides a, b and c as a consequence of the converse of the triangle inequality.
This converse appears in Euclid's Elements (Book I, Proposition 48): "If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right."[26]
It can be proved using the law of cosines or as follows:
Let ABC be a triangle with side lengths a, b, and c, with a2 + b2 = c2. Construct a second triangle with sides of length a and b containing a right angle. By the Pythagorean theorem, it follows that the hypotenuse of this triangle has length , the same as the hypotenuse of the first triangle. Since both triangles' sides are the same lengths a, b and c, the triangles are congruent and must have the same angles. Therefore, the angle between the side of lengths a and b in the original triangle is a right angle.
The above proof of the converse makes use of the Pythagorean theorem itself. The converse can also be proved without assuming the Pythagorean theorem.[27][28]
A corollary of the Pythagorean theorem's converse is a simple means of determining whether a triangle is right, obtuse, or acute, as follows. Let c be chosen to be the longest of the three sides and a + b > c (otherwise there is no triangle according to the triangle inequality). The following statements apply:[29]
- If a2 + b2 = c2, then the triangle is right.
- If a2 + b2 > c2, then the triangle is acute.
- If a2 + b2 < c2, then the triangle is obtuse.
Edsger W. Dijkstra has stated this proposition about acute, right, and obtuse triangles in this language: where α is the angle opposite to side a, β is the angle opposite to side b, γ is the angle opposite to side c, and sgn is the sign function.[30]
Remove ads
Consequences and uses of the theorem
Summarize
Perspective
Pythagorean triples
A Pythagorean triple has three positive integers a, b, and c, such that a2 + b2 = c2. In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths.[2] Such a triple is commonly written (a, b, c). Some well-known examples are (3, 4, 5) and (5, 12, 13).
A primitive Pythagorean triple is one in which a, b and c are coprime (the greatest common divisor of a, b, and c is 1).
The following is a list of primitive Pythagorean triples with values less than 100:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
There are many formulas for generating Pythagorean triples. Of these, Euclid's formula is the most well-known: given arbitrary positive integers m and n, the formula states that the integers forms a Pythagorean triple.
Inverse Pythagorean theorem
Given a right triangle with sides and altitude d (a line from the right angle and perpendicular to the hypotenuse c). The Pythagorean theorem has, while the inverse Pythagorean theorem relates the two legs a, b to the altitude d,[31] The equation can be transformed to, where x2 + y2 = z2 for any non-zero real x, y , z. If the a, b, d are to be integers, the smallest solution a > b > d is then using the smallest Pythagorean triple 3, 4, 5. The reciprocal Pythagorean theorem is a special case of the optic equation where the denominators are squares and also for a heptagonal triangle whose sides p, q, r are square numbers.
Incommensurable lengths

One of the consequences of the Pythagorean theorem is that line segments whose lengths are incommensurable (so the ratio of which is not a rational number) can be constructed using a straightedge and compass. Pythagoras's theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides by the square root operation.
The figure on the right shows how to construct line segments whose lengths are in the ratio of the square root of any positive integer.[32] Each triangle has a side (labeled "1") that is the chosen unit for measurement. In each right triangle, Pythagoras's theorem establishes the length of the hypotenuse in terms of this unit. If a hypotenuse is related to the unit by the square root of a positive integer that is not a perfect square, it is a realization of a length incommensurable with the unit, such as , , . For more detail, see Quadratic irrational.
Incommensurable lengths conflicted with the Pythagorean school's concept of numbers as only whole numbers. The Pythagorean school dealt with proportions by comparison of integer multiples of a common subunit.[33] According to one legend, Hippasus of Metapontum (c. 470 BC) was drowned at sea for making known the existence of the irrational or incommensurable.[34] Kurt von Fritz wrote a careful discussion of Hippasus's contributions.[35]
Complex numbers

For any complex number the absolute value or modulus is given by So the three quantities, r, x and y are related by the Pythagorean equation, Note that r is defined to be a positive number or zero but x and y can be negative as well as positive. Geometrically r is the distance of the z from zero or the origin O in the complex plane.
This can be generalised to find the distance between two points, z1 and z2 say. The required distance is given by so again they are related by a version of the Pythagorean equation,
Euclidean distance
The distance formula in Cartesian coordinates is derived from the Pythagorean theorem.[36] If (x1, y1) and (x2, y2) are points in the plane, then the distance between them, also called the Euclidean distance, is given by
More generally, in Euclidean n-space, the Euclidean distance between two points, and , is defined, by generalization of the Pythagorean theorem, as:
If instead of Euclidean distance, the square of this value (the squared Euclidean distance, or SED) is used, the resulting equation avoids square roots and is simply a sum of the SED of the coordinates:
The squared form is a smooth, convex function of both points, and is widely used in optimization theory and statistics, forming the basis of least squares.
Euclidean distance in other coordinate systems
If Cartesian coordinates are not used, for example, if polar coordinates are used in two dimensions or, in more general terms, if curvilinear coordinates are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the applications of Legendre polynomials in physics. The formulas can be discovered by using Pythagoras's theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates (r, θ) can be introduced as:
Then two points with locations (r1, θ1) and (r2, θ2) are separated by a distance s:
Performing the squares and combining terms, the Pythagorean formula for distance in Cartesian coordinates produces the separation in polar coordinates as: using the trigonometric product-to-sum formulas. This formula is the law of cosines, sometimes called the generalized Pythagorean theorem.[37] From this result, for the case where the radii to the two locations are at right angles, the enclosed angle Δθ = π/2, and the form corresponding to Pythagoras's theorem is regained: The Pythagorean theorem, valid for right triangles, therefore is a special case of the more general law of cosines, valid for arbitrary triangles.
Pythagorean trigonometric identity

In a right triangle with sides a, b and hypotenuse c, trigonometry determines the sine and cosine of the angle θ between side a and the hypotenuse as:
From that it follows: where the last step applies Pythagoras's theorem. This relation between sine and cosine is sometimes called the fundamental Pythagorean trigonometric identity.[38] In similar triangles, the ratios of the sides are the same regardless of the size of the triangles, and depend upon the angles. Consequently, in the figure, the triangle with hypotenuse of unit size has opposite side of size sin θ and adjacent side of size cos θ in units of the hypotenuse.
Relation to the cross product

The Pythagorean theorem relates the cross product and dot product in a similar way:[39]
This can be seen from the definitions of the cross product and dot product, as with n a unit vector normal to both a and b. The relationship follows from these definitions and the Pythagorean trigonometric identity.
This can also be used to define the cross product. By rearranging the following equation is obtained
This can be considered as a condition on the cross product and so part of its definition, for example in seven dimensions.[40][41]
As an axiom
If the first four of the Euclidean geometry axioms are assumed to be true then the Pythagorean theorem is equivalent to the fifth. That is, Euclid's fifth postulate implies the Pythagorean theorem and vice-versa.
Remove ads
Generalizations
Summarize
Perspective
Similar figures on the three sides
The Pythagorean theorem generalizes beyond the areas of squares on the three sides to any similar figures. This was known by Hippocrates of Chios in the 5th century BC,[42] and was included by Euclid in his Elements:[43]
If one erects similar figures (see Euclidean geometry) with corresponding sides on the sides of a right triangle, then the sum of the areas of the ones on the two smaller sides equals the area of the one on the larger side.
This extension assumes that the sides of the original triangle are the corresponding sides of the three congruent figures (so the common ratios of sides between the similar figures are a : b : c).[44] While Euclid's proof only applied to convex polygons, the theorem also applies to concave polygons and even to similar figures that have curved boundaries (but still with part of a figure's boundary being the side of the original triangle).[44]
The basic idea behind this generalization is that the area of a plane figure is proportional to the square of any linear dimension, and in particular is proportional to the square of the length of any side. Thus, if similar figures with areas A, B and C are erected on sides with corresponding lengths a, b and c then:
But, by the Pythagorean theorem, a2 + b2 = c2, so A + B = C.
Conversely, if we can prove that A + B = C for three similar figures without using the Pythagorean theorem, then we can work backwards to construct a proof of the theorem. For example, the starting center triangle can be replicated and used as a triangle C on its hypotenuse, and two similar right triangles (A and B ) constructed on the other two sides, formed by dividing the central triangle by its altitude. The sum of the areas of the two smaller triangles therefore is that of the third, thus A + B = C and reversing the above logic leads to the Pythagorean theorem a2 + b2 = c2. (See also Einstein's proof by dissection without rearrangement)
 green area A + B = blue area C |
 |
 |
Law of cosines

The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines, which states that where is the angle between sides and .[45]
When is radians or 90°, then , and the formula reduces to the usual Pythagorean theorem.
Arbitrary triangle

At any selected angle of a general triangle of sides a, b, c, inscribe an isosceles triangle such that the equal angles at its base θ are the same as the selected angle. Suppose the selected angle θ is opposite the side labeled c. Inscribing the isosceles triangle forms triangle CAD with angle θ opposite side b and with side r along c. A second triangle is formed with angle θ opposite side a and a side with length s along c, as shown in the figure. Thābit ibn Qurra stated that the sides of the three triangles were related as:[47][48] As the angle θ approaches π/2, the base of the isosceles triangle narrows, and lengths r and s overlap less and less. When θ = π/2, ADB becomes a right triangle, r + s = c, and the original Pythagorean theorem is regained.
One proof observes that triangle ABC has the same angles as triangle CAD, but in opposite order. (The two triangles share the angle at vertex A, both contain the angle θ, and so also have the same third angle by the triangle postulate.) Consequently, ABC is similar to the reflection of CAD, the triangle DAC in the lower panel. Taking the ratio of sides opposite and adjacent to θ, Likewise, for the reflection of the other triangle, Clearing fractions and adding these two relations: the required result.
The theorem remains valid if the angle θ is obtuse so the lengths r and s are non-overlapping.
General triangles using parallelograms

green area = blue area

Pappus's area theorem is a further generalization, that applies to triangles that are not right triangles, using parallelograms on the three sides in place of squares (squares are a special case, of course). The upper figure shows that for a scalene triangle, the area of the parallelogram on the longest side is the sum of the areas of the parallelograms on the other two sides, provided the parallelogram on the long side is constructed as indicated (the dimensions labeled with arrows are the same, and determine the sides of the bottom parallelogram). This replacement of squares with parallelograms bears a clear resemblance to the original Pythagoras's theorem, and was considered a generalization by Pappus of Alexandria in 4 AD[49][50]
The lower figure shows the elements of the proof. Focus on the left side of the figure. The left green parallelogram has the same area as the left, blue portion of the bottom parallelogram because both have the same base b and height h. However, the left green parallelogram also has the same area as the left green parallelogram of the upper figure, because they have the same base (the upper left side of the triangle) and the same height normal to that side of the triangle. Repeating the argument for the right side of the figure, the bottom parallelogram has the same area as the sum of the two green parallelograms.
Solid geometry


In terms of solid geometry, Pythagoras's theorem can be applied to three dimensions as follows. Consider the cuboid shown in the figure. The length of face diagonal AC is found from Pythagoras's theorem as:
where these three sides form a right triangle. Using diagonal AC and the horizontal edge CD, the length of body diagonal AD then is found by a second application of Pythagoras's theorem as: or, doing it all in one step:
This result is the three-dimensional expression for the magnitude of a vector v (the diagonal AD) in terms of its orthogonal components {vk} (the three mutually perpendicular sides):
This one-step formulation may be viewed as a generalization of Pythagoras's theorem to higher dimensions. However, this result is really just the repeated application of the original Pythagoras's theorem to a succession of right triangles in a sequence of orthogonal planes.
A substantial generalization of the Pythagorean theorem to three dimensions is de Gua's theorem, named for Jean Paul de Gua de Malves: If a tetrahedron has a right angle corner (like a corner of a cube), then the square of the area of the face opposite the right angle corner is the sum of the squares of the areas of the other three faces. This result can be generalized as in the "n-dimensional Pythagorean theorem":[51]
Let be orthogonal vectors in Rn. Consider the n-dimensional simplex S with vertices . (Think of the (n − 1)-dimensional simplex with vertices not including the origin as the "hypotenuse" of S and the remaining (n − 1)-dimensional faces of S as its "legs".) Then the square of the volume of the hypotenuse of S is the sum of the squares of the volumes of the n legs.
This statement is illustrated in three dimensions by the tetrahedron in the figure. The "hypotenuse" is the base of the tetrahedron at the back of the figure, and the "legs" are the three sides emanating from the vertex in the foreground. As the depth of the base from the vertex increases, the area of the "legs" increases, while that of the base is fixed. The theorem suggests that when this depth is at the value creating a right vertex, the generalization of Pythagoras's theorem applies. In a different wording:[52]
Given an n-rectangular n-dimensional simplex, the square of the (n − 1)-content of the facet opposing the right vertex will equal the sum of the squares of the (n − 1)-contents of the remaining facets.
Inner product spaces

The Pythagorean theorem can be generalized to inner product spaces,[53] which are generalizations of the familiar 2-dimensional and 3-dimensional Euclidean spaces. For example, a function may be considered as a vector with infinitely many components in an inner product space, as in functional analysis.[54]
In an inner product space, the concept of perpendicularity is replaced by the concept of orthogonality: two vectors v and w are orthogonal if their inner product is zero. The inner product is a generalization of the dot product of vectors. The dot product is called the standard inner product or the Euclidean inner product. However, other inner products are possible.[55]
The concept of length is replaced by the concept of the norm ‖v‖ of a vector v, defined as:[56]
In an inner-product space, the Pythagorean theorem states that for any two orthogonal vectors v and w we have Here the vectors v and w are akin to the sides of a right triangle with hypotenuse given by the vector sum v + w. This form of the Pythagorean theorem is a consequence of the properties of the inner product: where because of orthogonality.
A further generalization of the Pythagorean theorem in an inner product space to non-orthogonal vectors is the parallelogram law:[56]
which says that twice the sum of the squares of the lengths of the sides of a parallelogram is the sum of the squares of the lengths of the diagonals. Any norm that satisfies this equality is ipso facto a norm corresponding to an inner product.[56]
The Pythagorean identity can be extended to sums of more than two orthogonal vectors. If v1, v2, ..., vn are pairwise-orthogonal vectors in an inner-product space, then application of the Pythagorean theorem to successive pairs of these vectors (as described for 3-dimensions in the section on solid geometry) results in the equation[57]
Sets of m-dimensional objects in n-dimensional space
Another generalization of the Pythagorean theorem applies to Lebesgue-measurable sets of objects in any number of dimensions. Specifically, the square of the measure of an m-dimensional set of objects in one or more parallel m-dimensional flats in n-dimensional Euclidean space is equal to the sum of the squares of the measures of the orthogonal projections of the object(s) onto all m-dimensional coordinate subspaces.[58]
In mathematical terms: where:
- is a measure in m-dimensions (a length in one dimension, an area in two dimensions, a volume in three dimensions, etc.).
- is a set of one or more non-overlapping m-dimensional objects in one or more parallel m-dimensional flats in n-dimensional Euclidean space.
- is the total measure (sum) of the set of m-dimensional objects.
- represents an m-dimensional projection of the original set onto an orthogonal coordinate subspace.
- is the measure of the m-dimensional set projection onto m-dimensional coordinate subspace i. Because object projections can overlap on a coordinate subspace, the measure of each object projection in the set must be calculated individually, then measures of all projections added together to provide the total measure for the set of projections on the given coordinate subspace.
- is the number of orthogonal, m-dimensional coordinate subspaces in n-dimensional space (Rn) onto which the m-dimensional objects are projected (m ≤ n):
Non-Euclidean geometry
The Pythagorean theorem is derived from the axioms of Euclidean geometry, and in fact, were the Pythagorean theorem to fail for some right triangle, then the plane in which this triangle is contained cannot be Euclidean. More precisely, the Pythagorean theorem implies, and is implied by, Euclid's Parallel (Fifth) Postulate.[59][60] Thus, right triangles in a non-Euclidean geometry[61] do not satisfy the Pythagorean theorem. For example, in spherical geometry, all three sides of the right triangle (say a, b, and c) bounding an octant of the unit sphere have length equal to π/2, and all its angles are right angles, which violates the Pythagorean theorem because a2 + b2 = 2c2 > c2.
Here two cases of non-Euclidean geometry are considered—spherical geometry and hyperbolic plane geometry; in each case, as in the Euclidean case for non-right triangles, the result replacing the Pythagorean theorem follows from the appropriate law of cosines.
However, the Pythagorean theorem remains true in hyperbolic geometry and elliptic geometry if the condition that the triangle be right is replaced with the condition that two of the angles sum to the third, say A + B = C. The sides are then related as follows: the sum of the areas of the circles with diameters a and b equals the area of the circle with diameter c.[62]
Spherical geometry

For any right triangle on a sphere of radius R (for example, if γ in the figure is a right angle), with sides a, b, and c, the relation between the sides takes the form:[63]
This equation can be derived as a special case of the spherical law of cosines that applies to all spherical triangles:
For infinitesimal triangles on the sphere (or equivalently, for finite spherical triangles on a sphere of infinite radius), the spherical relation between the sides of a right triangle reduces to the Euclidean form of the Pythagorean theorem. To see how, assume we have a spherical triangle of fixed side lengths a, b, and c on a sphere with expanding radius R. As R approaches infinity the quantities a/R, b/R, and c/R tend to zero and the spherical Pythagorean identity reduces to {{{1}}}, so we must look at its asymptotic expansion.
The Maclaurin series for the cosine function can be written as with the remainder term in big O notation. Letting be a side of the triangle, and treating the expression as an asymptotic expansion in terms of R for a fixed c,
and likewise for a and b. Substituting the asymptotic expansion for each of the cosines into the spherical relation for a right triangle yields
Subtracting 1 and then negating each side,
Multiplying through by 2R2, the asymptotic expansion for c in terms of fixed a, b and variable R is
The Euclidean Pythagorean relationship is recovered in the limit, as the remainder vanishes when the radius R approaches infinity.
For practical computation in spherical trigonometry with small right triangles, cosines can be replaced with sines using the double-angle identity to avoid loss of significance. Then the spherical Pythagorean theorem can alternately be written as
Hyperbolic geometry

In a hyperbolic space with uniform Gaussian curvature −1/R2, for a right triangle with legs a, b, and hypotenuse c, the relation between the sides takes the form:[64]
where cosh is the hyperbolic cosine. This formula is a special form of the hyperbolic law of cosines that applies to all hyperbolic triangles:[65] with γ the angle at the vertex opposite the side c.
By using the Maclaurin series for the hyperbolic cosine, cosh x ≈ 1 + x2/2, it can be shown that as a hyperbolic triangle becomes very small (that is, as a, b, and c all approach zero), the hyperbolic relation for a right triangle approaches the form of Pythagoras's theorem.
For small right triangles (a, b ≪ R), the hyperbolic cosines can be eliminated to avoid loss of significance, giving
Very small triangles
For any uniform curvature K (positive, zero, or negative), in very small right triangles (|K|a2, |K|b2 ≪ 1) with hypotenuse c, it can be shown that
Differential geometry

The Pythagorean theorem applies to infinitesimal triangles seen in differential geometry. In three dimensional space, the distance between two infinitesimally separated points satisfies
with ds the element of distance and (dx, dy, dz) the components of the vector separating the two points. Such a space is called a Euclidean space. However, in Riemannian geometry, a generalization of this expression useful for general coordinates (not just Cartesian) and general spaces (not just Euclidean) takes the form:[66]
which is called the metric tensor.[b] It may be a function of position, and often describes curved space. A simple example is Euclidean (flat) space expressed in curvilinear coordinates. For example, in polar coordinates:
Remove ads
History
Summarize
Perspective

There is debate whether the Pythagorean theorem was discovered once, or many times in many places, and the date of first discovery is uncertain, as is the date of the first proof. The history of the theorem can be divided into four parts: knowledge of Pythagorean triples, knowledge of the relationship among the sides of a right triangle, knowledge of the relationships among adjacent angles, and proofs of the theorem within some deductive system.
Written c. 1800 BC, the Egyptian Middle Kingdom Berlin Papyrus 6619 includes a problem whose solution is the Pythagorean triple 6:8:10, but the problem does not mention a triangle. According to Plutarch, the ancient Egyptians did know about the 3:4:5 right triangle, identifying its sides with Osiris, Isis, and Horus respectively.[68]
Historians of Mesopotamian mathematics have concluded that the Pythagorean rule was in widespread use during the Old Babylonian period (20th to 16th centuries BC), over a thousand years before Pythagoras was born.[69][70][71][72] The Mesopotamian tablet Plimpton 322, written near Larsa also c. 1800 BC, contains entries that can be interpreted as the sides and diagonals of 15 different Pythagorean triples.[73] Another tablet from a similar time, YBC 7289, calculates the diagonal of a square or, equivalently, or an isosceles right triangle.[74]
In India, the Baudhayana Shulba Sutra, the dates of which are given variously as between the 8th and 5th century BC,[75] contains a list of Pythagorean triples and a statement of the Pythagorean theorem, both in the special case of the isosceles right triangle and in the general case, as does the Apastamba Shulba Sutra (c. 600 BC).[c]
Byzantine Neoplatonic philosopher and mathematician Proclus, writing in the fifth century AD, states two arithmetic rules, "one of them attributed to Plato, the other to Pythagoras",[77] for generating special Pythagorean triples. The rule attributed to Pythagoras (c. 570 – c. 495 BC) starts from an odd number and produces a triple with leg and hypotenuse differing by one unit; the rule attributed to Plato (428/427 or 424/423 – 348/347 BC) starts from an even number and produces a triple with leg and hypotenuse differing by two units. According to Thomas L. Heath (1861–1940), no specific attribution of the theorem to Pythagoras exists in the surviving Greek literature from the five centuries after Pythagoras lived.[78] However, when authors such as Plutarch and Cicero attributed the theorem to Pythagoras, they did so in a way which suggests that the attribution was widely known and undoubted.[79][80] Classicist Kurt von Fritz wrote, "Whether this formula is rightly attributed to Pythagoras personally ... one can safely assume that it belongs to the very oldest period of Pythagorean mathematics."[81] Around 300 BC, in Euclid's Elements, the oldest extant axiomatic proof of the theorem is presented.[82]
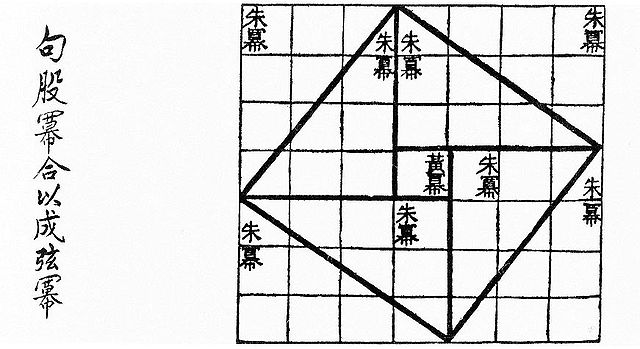
With contents known much earlier, but in surviving texts dating from roughly the 1st century BC, the Chinese text Zhoubi Suanjing (周髀算经), (The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven) gives a reasoning for the Pythagorean theorem for the (3, 4, 5) triangle — in China it is called the "Gougu theorem" (勾股定理).[83][84] During the Han Dynasty (202 BC to 220 AD), Pythagorean triples appear in The Nine Chapters on the Mathematical Art,[85] together with a mention of right triangles.[86] Some believe the theorem arose first in China in the 11th century BC,[87] where it is alternatively known as the "Shang Gao theorem" (商高定理),[88] named after the Duke of Zhou's astronomer and mathematician, whose reasoning composed most of what was in the Zhoubi Suanjing.[89]
Remove ads
See also
- Addition in quadrature
- At Dulcarnon – English phrase – at the end of one's wits
- British flag theorem
- Bride's Chair – Illustration of the Pythagorean theorem
- Fermat's Last Theorem
- Garfield's proof of the Pythagorean theorem
- Hsuan thu – Ancient Chinese diagram using the 3,4,5 right triangle to demonstrate the Pythagorean theorem
- Inverse Pythagorean theorem
- Kepler triangle
- Linear algebra
- List of triangle topics
- Lp space
- Nonhypotenuse number
- Parallelogram law
- Parseval's identity – The energy of a periodic function is the same in the time and frequency domain.
- Ptolemy's theorem – Relates the 4 sides and 2 diagonals of a quadrilateral with vertices on a common circle
- Pythagoras in popular culture
- Pythagorean expectation
- Pythagorean hodograph curve – determined by polynomials that obey the Pythagorean theorem
- Pythagorean tiling
- Rational trigonometry in Pythagoras's theorem
- Thales theorem – On triangles inscribed in a circle with a diameter as an edge
Remove ads
Notes and references
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads





































































![{\displaystyle {\begin{aligned}\left\|\mathbf {v} +\mathbf {w} \right\|^{2}&=\langle \mathbf {v+w} ,\ \mathbf {v+w} \rangle \\[3mu]&=\langle \mathbf {v} ,\,\mathbf {v} \rangle +\langle \mathbf {w} ,\,\mathbf {w} \rangle +\langle \mathbf {v,\,w} \rangle +\langle \mathbf {w,\,v} \rangle \\[3mu]&=\left\|\mathbf {v} \right\|^{2}+\left\|\mathbf {w} \right\|^{2},\end{aligned}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/4a87ac0a2ee01e7540ac5d4409de31fd61466002)




























