Top Qs
Timeline
Chat
Perspective
Riemannian manifold
Smooth manifold with an inner product on each tangent space From Wikipedia, the free encyclopedia
Remove ads
In differential geometry, a Riemannian manifold is a geometric space on which many geometric notions such as distance, angles, length, volume, and curvature are defined. Euclidean space, the -sphere, hyperbolic space, and smooth surfaces in three-dimensional space, such as ellipsoids and paraboloids, are all examples of Riemannian manifolds. Riemannian manifolds are named after German mathematician Bernhard Riemann, who first conceptualized them.

Formally, a Riemannian metric (or just a metric) on a smooth manifold is a smoothly varying choice of inner product for each tangent space of the manifold. A Riemannian manifold is a smooth manifold together with a Riemannian metric. The techniques of differential and integral calculus are used to pull geometric data out of the Riemannian metric. For example, integration leads to the Riemannian distance function, whereas differentiation is used to define curvature and parallel transport.
Any smooth surface in three-dimensional Euclidean space is a Riemannian manifold with a Riemannian metric coming from the way it sits inside the ambient space. The same is true for any submanifold of Euclidean space of any dimension. Although John Nash proved that every Riemannian manifold arises as a submanifold of Euclidean space, and although some Riemannian manifolds are naturally exhibited or defined in that way, the idea of a Riemannian manifold emphasizes the intrinsic point of view, which defines geometric notions directly on the abstract space itself without referencing an ambient space. In many instances, such as for hyperbolic space and projective space, Riemannian metrics are more naturally defined or constructed using the intrinsic point of view. Additionally, many metrics on Lie groups and homogeneous spaces are defined intrinsically by using group actions to transport an inner product on a single tangent space to the entire manifold, and many special metrics such as constant scalar curvature metrics and Kähler–Einstein metrics are constructed intrinsically using tools from partial differential equations.
Riemannian geometry, the study of Riemannian manifolds, has deep connections to other areas of math, including geometric topology, complex geometry, and algebraic geometry. Applications include physics (especially general relativity and gauge theory), computer graphics, machine learning, and cartography. Generalizations of Riemannian manifolds include pseudo-Riemannian manifolds, Finsler manifolds, and sub-Riemannian manifolds.
Remove ads
History
Summarize
Perspective

In 1827, Carl Friedrich Gauss discovered that the Gaussian curvature of a surface embedded in 3-dimensional space only depends on local measurements made within the surface (the first fundamental form).[1] This result is known as the Theorema Egregium ("remarkable theorem" in Latin).
A map that preserves the local measurements of a surface is called a local isometry. A property of a surface is called an intrinsic property if it is preserved by local isometries and it is called an extrinsic property if it is not. In this language, the Theorema Egregium says that the Gaussian curvature is an intrinsic property of surfaces.
Riemannian manifolds and their curvature were first introduced non-rigorously by Bernhard Riemann in 1854.[2] However, they would not be formalized until much later. In fact, the more primitive concept of a smooth manifold was first explicitly defined only in 1913 in a book by Hermann Weyl.[2]
Élie Cartan introduced the Cartan connection, one of the first concepts of a connection. Levi-Civita defined the Levi-Civita connection, a special connection on a Riemannian manifold.
Albert Einstein used the theory of pseudo-Riemannian manifolds (a generalization of Riemannian manifolds) to develop general relativity. Specifically, the Einstein field equations are constraints on the curvature of spacetime, which is a 4-dimensional pseudo-Riemannian manifold.
Remove ads
Definition
Summarize
Perspective
Riemannian metrics and Riemannian manifolds

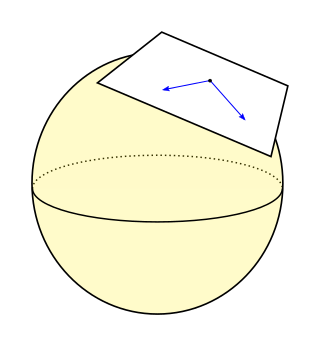
Let be a smooth manifold. For each point , there is an associated vector space called the tangent space of at . Vectors in are thought of as the vectors tangent to at .
However, does not come equipped with an inner product, a "measuring stick" that gives tangent vectors a concept of length and angle. This is an important deficiency because calculus teaches that to calculate the length of a curve, the length of vectors tangent to the curve must be defined. A Riemannian metric puts such a "measuring stick" on every tangent space.
A Riemannian metric on assigns to each a positive-definite symmetric bilinear form (i.e. an inner product) in a smooth way (see the section on regularity below).[3] This induces a norm defined by . A smooth manifold endowed with a Riemannian metric is a Riemannian manifold, denoted .[3] A Riemannian metric is a special case of a metric tensor.
A Riemannian metric is not to be confused with the distance function of a metric space, which is also called a metric.
The Riemannian metric in coordinates
If are smooth local coordinates on , the vectors
form a basis of the vector space for any . Relative to this basis, one can define the Riemannian metric's components at each point by
- .[4]
These functions can be put together into an matrix-valued function on . The requirement that is a positive-definite inner product then says exactly that this matrix-valued function is a symmetric positive-definite matrix at .
In terms of the tensor algebra, the Riemannian metric can be written in terms of the dual basis of the cotangent bundle as
Regularity of the Riemannian metric
The Riemannian metric is continuous if its components are continuous in any smooth coordinate chart The Riemannian metric is smooth if its components are smooth in any smooth coordinate chart. One can consider many other types of Riemannian metrics in this spirit, such as Lipschitz Riemannian metrics or measurable Riemannian metrics.
There are situations in geometric analysis in which one wants to consider non-smooth Riemannian metrics. See for instance (Gromov 1999) and (Shi and Tam 2002). However, in this article, is assumed to be smooth unless stated otherwise.
Musical isomorphism
In analogy to how an inner product on a vector space induces an isomorphism between a vector space and its dual given by , a Riemannian metric induces an isomorphism of bundles between the tangent bundle and the cotangent bundle. Namely, if is a Riemannian metric, then
is a isomorphism of smooth vector bundles from the tangent bundle to the cotangent bundle .[5]
Isometries
An isometry is a function between Riemannian manifolds which preserves all of the structure of Riemannian manifolds. If two Riemannian manifolds have an isometry between them, they are called isometric, and they are considered to be the same manifold for the purpose of Riemannian geometry.
Specifically, if and are two Riemannian manifolds, a diffeomorphism is called an isometry if ,[6] that is, if
for all and For example, translations and rotations are both isometries from Euclidean space (to be defined soon) to itself.
One says that a smooth map not assumed to be a diffeomorphism, is a local isometry if every has an open neighborhood such that is an isometry (and thus a diffeomorphism).[6]
Volume
An oriented -dimensional Riemannian manifold has a unique -form called the Riemannian volume form.[7] The Riemannian volume form is preserved by orientation-preserving isometries.[8] The volume form gives rise to a measure on which allows measurable functions to be integrated.[citation needed] If is compact, the volume of is .[7]
Remove ads
Examples
Summarize
Perspective
Euclidean space
Let denote the standard coordinates on The (canonical) Euclidean metric is given by[9]
or equivalently
or equivalently by its coordinate functions
- where is the Kronecker delta
which together form the matrix
The Riemannian manifold is called Euclidean space.
Submanifolds

Let be a Riemannian manifold and let be an immersed submanifold or an embedded submanifold of . The pullback of is a Riemannian metric on , and is said to be a Riemannian submanifold of .[10]
In the case where , the map is given by and the metric is just the restriction of to vectors tangent along . In general, the formula for is
where is the pushforward of by
Examples:
- The -sphere
- is a smooth embedded submanifold of Euclidean space .[11] The Riemannian metric this induces on is called the round metric or standard metric.
- Fix real numbers . The ellipsoid
- is a smooth embedded submanifold of Euclidean space .
- The graph of a smooth function is a smooth embedded submanifold of with its standard metric.
- If is not simply connected, there is a covering map , where is the universal cover of . This is an immersion (since it is locally a diffeomorphism), so automatically inherits a Riemannian metric. By the same principle, any smooth covering space of a Riemannian manifold inherits a Riemannian metric.
On the other hand, if already has a Riemannian metric , then the immersion (or embedding) is called an isometric immersion (or isometric embedding) if . Hence isometric immersions and isometric embeddings are Riemannian submanifolds.[10]
Products
A torus naturally carries a Euclidean metric, obtained by identifying opposite sides of a square (left). The resulting Riemannian manifold, called a flat torus, cannot be isometrically embedded in 3-dimensional Euclidean space (right), because it is necessary to bend and stretch the sheet in doing so. Thus the intrinsic geometry of a flat torus is different from that of an embedded torus.
Let and be two Riemannian manifolds, and consider the product manifold . The Riemannian metrics and naturally put a Riemannian metric on which can be described in a few ways.
- Considering the decomposition one may define
- If is a smooth coordinate chart on and is a smooth coordinate chart on , then is a smooth coordinate chart on Let be the representation of in the chart and let be the representation of in the chart . The representation of in the coordinates is
- where [12]
For example, consider the -torus . If each copy of is given the round metric, the product Riemannian manifold is called the flat torus. As another example, the Riemannian product , where each copy of has the Euclidean metric, is isometric to with the Euclidean metric.
Positive combinations of metrics
Let be Riemannian metrics on If are any positive smooth functions on , then is another Riemannian metric on
Remove ads
Every smooth manifold admits a Riemannian metric
Summarize
Perspective
Theorem: Every smooth manifold admits a (non-canonical) Riemannian metric.[13]
This is a fundamental result. Although much of the basic theory of Riemannian metrics can be developed using only that a smooth manifold is a locally Euclidean topological space, for this result it is necessary to use that smooth manifolds are Hausdorff and paracompact. The reason is that the proof makes use of a partition of unity.
An alternative proof uses the Whitney embedding theorem to embed into Euclidean space and then pulls back the metric from Euclidean space to . On the other hand, the Nash embedding theorem states that, given any smooth Riemannian manifold there is an embedding for some such that the pullback by of the standard Riemannian metric on is That is, the entire structure of a smooth Riemannian manifold can be encoded by a diffeomorphism to a certain embedded submanifold of some Euclidean space. Therefore, one could argue that nothing can be gained from the consideration of abstract smooth manifolds and their Riemannian metrics. However, there are many natural smooth Riemannian manifolds, such as the set of rotations of three-dimensional space and hyperbolic space, of which any representation as a submanifold of Euclidean space will fail to represent their remarkable symmetries and properties as clearly as their abstract presentations do.
Remove ads
Metric space structure
Summarize
Perspective
An admissible curve is a piecewise smooth curve whose velocity is nonzero everywhere it is defined. The nonnegative function is defined on the interval except for at finitely many points. The length of an admissible curve is defined as
The integrand is bounded and continuous except at finitely many points, so it is integrable. For a connected Riemannian manifold, define by
Theorem: is a metric space, and the metric topology on coincides with the topology on .[14]
Although the length of a curve is given by an explicit formula, it is generally impossible to write out the distance function by any explicit means. In fact, if is compact, there always exist points where is non-differentiable, and it can be remarkably difficult to even determine the location or nature of these points, even in seemingly simple cases such as when is an ellipsoid.[citation needed]
If one works with Riemannian metrics that are merely continuous but possibly not smooth, the length of an admissible curve and the Riemannian distance function are defined exactly the same, and, as before, is a metric space and the metric topology on coincides with the topology on .[15]
Diameter
The diameter of the metric space is
The Hopf–Rinow theorem shows that if is complete and has finite diameter, it is compact. Conversely, if is compact, then the function has a maximum, since it is a continuous function on a compact metric space. This proves the following.
- If is complete, then it is compact if and only if it has finite diameter.
This is not the case without the completeness assumption; for counterexamples one could consider any open bounded subset of a Euclidean space with the standard Riemannian metric. It is also not true that any complete metric space of finite diameter must be compact; it matters that the metric space came from a Riemannian manifold.
Remove ads
Connections, geodesics, and curvature
Summarize
Perspective
Connections
An (affine) connection is an additional structure on a Riemannian manifold that defines differentiation of one vector field with respect to another. Connections contain geometric data, and two Riemannian manifolds with different connections have different geometry.
Let denote the space of vector fields on . An (affine) connection
on is a bilinear map such that
- For every function ,
- The product rule holds.[16]
The expression is called the covariant derivative of with respect to .
Levi-Civita connection
Two Riemannian manifolds with different connections have different geometry. Thankfully, there is a natural connection associated to a Riemannian manifold called the Levi-Civita connection.
A connection is said to preserve the metric if
A connection is torsion-free if
where is the Lie bracket.
A Levi-Civita connection is a torsion-free connection that preserves the metric. Once a Riemannian metric is fixed, there exists a unique Levi-Civita connection.[17] Note that the definition of preserving the metric uses the regularity of .
Covariant derivative along a curve
If is a smooth curve, a smooth vector field along is a smooth map such that for all . The set of smooth vector fields along is a vector space under pointwise vector addition and scalar multiplication.[18] One can also pointwise multiply a smooth vector field along by a smooth function :
- for
Let be a smooth vector field along . If is a smooth vector field on a neighborhood of the image of such that , then is called an extension of .
Given a fixed connection on and a smooth curve , there is a unique operator , called the covariant derivative along , such that:[19]
- If is an extension of , then .
Geodesics
In Euclidean space (left), the maximal geodesics are straight lines. In the round sphere (right), the maximal geodesics are great circles.
Geodesics are curves with no intrinsic acceleration. Equivalently, geodesics are curves that locally take the shortest path between two points. They are the generalization of straight lines in Euclidean space to arbitrary Riemannian manifolds. An ant living in a Riemannian manifold walking straight ahead without making any effort to accelerate or turn would trace out a geodesic.
Fix a connection on . Let be a smooth curve. The acceleration of is the vector field along . If for all , is called a geodesic.[20]
For every and , there exists a geodesic defined on some open interval containing 0 such that and . Any two such geodesics agree on their common domain.[21] Taking the union over all open intervals containing 0 on which a geodesic satisfying and exists, one obtains a geodesic called a maximal geodesic of which every geodesic satisfying and is a restriction.[22]
Every curve that has the shortest length of any admissible curve with the same endpoints as is a geodesic (in a unit-speed reparameterization).[23]
Examples
- The nonconstant maximal geodesics of the Euclidean plane are exactly the straight lines.[22] This agrees with the fact from Euclidean geometry that the shortest path between two points is a straight line segment.
- The nonconstant maximal geodesics of with the round metric are exactly the great circles.[24] Since the Earth is approximately a sphere, this means that the shortest path a plane can fly between two locations on Earth is a segment of a great circle.
Hopf–Rinow theorem

The Riemannian manifold with its Levi-Civita connection is geodesically complete if the domain of every maximal geodesic is .[25] The plane is geodesically complete. On the other hand, the punctured plane with the restriction of the Riemannian metric from is not geodesically complete as the maximal geodesic with initial conditions , does not have domain .
The Hopf–Rinow theorem characterizes geodesically complete manifolds.
Theorem: Let be a connected Riemannian manifold. The following are equivalent:[26]
- The metric space is complete (every -Cauchy sequence converges),
- All closed and bounded subsets of are compact,
- is geodesically complete.
Parallel transport

In Euclidean space, all tangent spaces are canonically identified with each other via translation, so it is easy to move vectors from one tangent space to another. Parallel transport is a way of moving vectors from one tangent space to another along a curve in the setting of a general Riemannian manifold. Given a fixed connection, there is a unique way to do parallel transport.[27]
Specifically, call a smooth vector field along a smooth curve parallel along if identically.[22] Fix a curve with and . to parallel transport a vector to a vector in along , first extend to a vector field parallel along , and then take the value of this vector field at .
The images below show parallel transport induced by the Levi-Civita connection associated to two different Riemannian metrics on the punctured plane . The curve the parallel transport is done along is the unit circle. In polar coordinates, the metric on the left is the standard Euclidean metric , while the metric on the right is . This second metric has a singularity at the origin, so it does not extend past the puncture, but the first metric extends to the entire plane.
Warning: This is parallel transport on the punctured plane along the unit circle, not parallel transport on the unit circle. Indeed, in the first image, the vectors fall outside of the tangent space to the unit circle.
Riemann curvature tensor
The Riemann curvature tensor measures precisely the extent to which parallel transporting vectors around a small rectangle is not the identity map.[28] The Riemann curvature tensor is 0 at every point if and only if the manifold is locally isometric to Euclidean space.[29]
Fix a connection on . The Riemann curvature tensor is the map defined by
where is the Lie bracket of vector fields. The Riemann curvature tensor is a -tensor field.[30]
Ricci curvature tensor
Fix a connection on . The Ricci curvature tensor is
where is the trace. The Ricci curvature tensor is a covariant 2-tensor field.[31]
Einstein manifolds
The Ricci curvature tensor plays a defining role in the theory of Einstein manifolds, which has applications to the study of gravity. A (pseudo-)Riemannian metric is called an Einstein metric if Einstein's equation
- for some constant
holds, and a (pseudo-)Riemannian manifold whose metric is Einstein is called an Einstein manifold.[32] Examples of Einstein manifolds include Euclidean space, the -sphere, hyperbolic space, and complex projective space with the Fubini-Study metric.
Scalar curvature
Remove ads
Constant curvature and space forms
Summarize
Perspective
A Riemannian manifold is said to have constant curvature κ if every sectional curvature equals the number κ. This is equivalent to the condition that, relative to any coordinate chart, the Riemann curvature tensor can be expressed in terms of the metric tensor as
This implies that the Ricci curvature is given by Rjk = (n − 1)κgjk and the scalar curvature is n(n − 1)κ, where n is the dimension of the manifold. In particular, every Riemannian manifold of constant curvature is an Einstein manifold, thereby having constant scalar curvature. As found by Bernhard Riemann in his 1854 lecture introducing Riemannian geometry, the locally defined Riemannian metric
has constant curvature κ. Any two Riemannian manifolds of the same constant curvature are locally isometric, and so it follows that any Riemannian manifold of constant curvature κ can be covered by coordinate charts relative to which the metric has the above form.[33]
A Riemannian space form is a Riemannian manifold with constant curvature which is additionally connected and geodesically complete. A Riemannian space form is said to be a spherical space form if the curvature is positive, a Euclidean space form if the curvature is zero, and a hyperbolic space form or hyperbolic manifold if the curvature is negative. In any dimension, the sphere with its standard Riemannian metric, Euclidean space, and hyperbolic space are Riemannian space forms of constant curvature 1, 0, and −1 respectively. Furthermore, the Killing–Hopf theorem says that any simply connected spherical space form is homothetic to the sphere, any simply connected Euclidean space form is homothetic to Euclidean space, and any simply connected hyperbolic space form is homothetic to hyperbolic space.[33]
Using the covering manifold construction, any Riemannian space form is isometric to the quotient manifold of a simply connected Riemannian space form, modulo a certain group action of isometries. For example, the isometry group of the n-sphere is the orthogonal group O(n + 1). Given any finite subgroup G thereof in which only the identity matrix possesses 1 as an eigenvalue, the natural group action of the orthogonal group on the n-sphere restricts to a group action of G, with the quotient manifold Sn / G inheriting a geodesically complete Riemannian metric of constant curvature 1. Up to homothety, every spherical space form arises in this way; this largely reduces the study of spherical space forms to problems in group theory. For instance, this can be used to show directly that every even-dimensional spherical space form is homothetic to the standard metric on either the sphere or real projective space. There are many more odd-dimensional spherical space forms, although there are known algorithms for their classification. The list of three-dimensional spherical space forms is infinite but explicitly known, and includes the lens spaces and the Poincaré dodecahedral space.[34]
The case of Euclidean and hyperbolic space forms can likewise be reduced to group theory, based on study of the isometry group of Euclidean space and hyperbolic space. For example, the class of two-dimensional Euclidean space forms includes Riemannian metrics on the Klein bottle, the Möbius strip, the torus, the cylinder S1 × ℝ, along with the Euclidean plane. Unlike the case of two-dimensional spherical space forms, in some cases two space form structures on the same manifold are not homothetic. The case of two-dimensional hyperbolic space forms is even more complicated, having to do with Teichmüller space. In three dimensions, the Euclidean space forms are known, while the geometry of hyperbolic space forms in three and higher dimensions remains an area of active research known as hyperbolic geometry.[35]
Remove ads
Riemannian metrics on Lie groups
Summarize
Perspective
Left-invariant metrics on Lie groups
Let G be a Lie group, such as the group of rotations in three-dimensional space. Using the group structure, any inner product on the tangent space at the identity (or any other particular tangent space) can be transported to all other tangent spaces to define a Riemannian metric. Formally, given an inner product ge on the tangent space at the identity, the inner product on the tangent space at an arbitrary point p is defined by
where for arbitrary x, Lx is the left multiplication map G → G sending a point y to xy. Riemannian metrics constructed this way are left-invariant; right-invariant Riemannian metrics could be constructed likewise using the right multiplication map instead.
The Levi-Civita connection and curvature of a general left-invariant Riemannian metric can be computed explicitly in terms of ge, the adjoint representation of G, and the Lie algebra associated to G.[36] These formulas simplify considerably in the special case of a Riemannian metric which is bi-invariant (that is, simultaneously left- and right-invariant).[37] All left-invariant metrics have constant scalar curvature.
Left- and bi-invariant metrics on Lie groups are an important source of examples of Riemannian manifolds. Berger spheres, constructed as left-invariant metrics on the special unitary group SU(2), are among the simplest examples of the collapsing phenomena, in which a simply connected Riemannian manifold can have small volume without having large curvature.[38] They also give an example of a Riemannian metric which has constant scalar curvature but which is not Einstein, or even of parallel Ricci curvature.[39] Hyperbolic space can be given a Lie group structure relative to which the metric is left-invariant.[40][41] Any bi-invariant Riemannian metric on a Lie group has nonnegative sectional curvature, giving a variety of such metrics: a Lie group can be given a bi-invariant Riemannian metric if and only if it is the product of a compact Lie group with an abelian Lie group.[42]
Homogeneous spaces
A Riemannian manifold (M, g) is said to be homogeneous if for every pair of points x and y in M, there is some isometry f of the Riemannian manifold sending x to y. This can be rephrased in the language of group actions as the requirement that the natural action of the isometry group is transitive. Every homogeneous Riemannian manifold is geodesically complete and has constant scalar curvature.[43]
Up to isometry, all homogeneous Riemannian manifolds arise by the following construction. Given a Lie group G with compact subgroup K which does not contain any nontrivial normal subgroup of G, fix any complemented subspace W of the Lie algebra of K within the Lie algebra of G. If this subspace is invariant under the linear map adG(k): W → W for any element k of K, then G-invariant Riemannian metrics on the coset space G/K are in one-to-one correspondence with those inner products on W which are invariant under adG(k): W → W for every element k of K.[44] Each such Riemannian metric is homogeneous, with G naturally viewed as a subgroup of the full isometry group.
The above example of Lie groups with left-invariant Riemannian metrics arises as a very special case of this construction, namely when K is the trivial subgroup containing only the identity element. The calculations of the Levi-Civita connection and the curvature referenced there can be generalized to this context, where now the computations are formulated in terms of the inner product on W, the Lie algebra of G, and the direct sum decomposition of the Lie algebra of G into the Lie algebra of K and W.[44] This reduces the study of the curvature of homogeneous Riemannian manifolds largely to algebraic problems. This reduction, together with the flexibility of the above construction, makes the class of homogeneous Riemannian manifolds very useful for constructing examples.
Symmetric spaces
A connected Riemannian manifold (M, g) is said to be symmetric if for every point p of M there exists some isometry of the manifold with p as a fixed point and for which the negation of the differential at p is the identity map. Every Riemannian symmetric space is homogeneous, and consequently is geodesically complete and has constant scalar curvature. However, Riemannian symmetric spaces also have a much stronger curvature property not possessed by most homogeneous Riemannian manifolds, namely that the Riemann curvature tensor and Ricci curvature are parallel. Riemannian manifolds with this curvature property, which could loosely be phrased as "constant Riemann curvature tensor" (not to be confused with constant curvature), are said to be locally symmetric. This property nearly characterizes symmetric spaces; Élie Cartan proved in the 1920s that a locally symmetric Riemannian manifold which is geodesically complete and simply-connected must in fact be symmetric.[45]
Many of the fundamental examples of Riemannian manifolds are symmetric. The most basic include the sphere and real projective spaces with their standard metrics, along with hyperbolic space. The complex projective space, quaternionic projective space, and Cayley plane are analogues of the real projective space which are also symmetric, as are complex hyperbolic space, quaternionic hyperbolic space, and Cayley hyperbolic space, which are instead analogues of hyperbolic space. Grassmannian manifolds also carry natural Riemannian metrics making them into symmetric spaces. Among the Lie groups with left-invariant Riemannian metrics, those which are bi-invariant are symmetric.[45]
Based on their algebraic formulation as special kinds of homogeneous spaces, Cartan achieved an explicit classification of symmetric spaces which are irreducible, referring to those which cannot be locally decomposed as product spaces. Every such space is an example of an Einstein manifold; among them only the one-dimensional manifolds have zero scalar curvature. These spaces are important from the perspective of Riemannian holonomy. As found in the 1950s by Marcel Berger, any Riemannian manifold which is simply connected and irreducible is either a symmetric space or has Riemannian holonomy belonging to a list of only seven possibilities. Six of the seven exceptions to symmetric spaces in Berger's classification fall into the fields of Kähler geometry, quaternion-Kähler geometry, G2 geometry, and Spin(7) geometry, each of which study Riemannian manifolds equipped with certain extra structures and symmetries. The seventh exception is the study of 'generic' Riemannian manifolds with no particular symmetry, as reflected by the maximal possible holonomy group.[45]
Remove ads
Infinite-dimensional manifolds
Summarize
Perspective
This section includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (July 2024) |
The statements and theorems above are for finite-dimensional manifolds—manifolds whose charts map to open subsets of These can be extended, to a certain degree, to infinite-dimensional manifolds; that is, manifolds that are modeled after a topological vector space; for example, Fréchet, Banach, and Hilbert manifolds.
Definitions
Riemannian metrics are defined in a way similar to the finite-dimensional case. However, there is a distinction between two types of Riemannian metrics:
- A weak Riemannian metric on is a smooth function such that for any the restriction is an inner product on [citation needed]
- A strong Riemannian metric on is a weak Riemannian metric such that induces the topology on . If is a strong Riemannian metric, then must be a Hilbert manifold.[citation needed]
Examples
- If is a Hilbert space, then for any one can identify with The metric for all is a strong Riemannian metric.[citation needed]
- Let be a compact Riemannian manifold and denote by its diffeomorphism group. The latter is a smooth manifold (see here) and in fact, a Lie group.[citation needed] Its tangent bundle at the identity is the set of smooth vector fields on [citation needed] Let be a volume form on The weak Riemannian metric on , denoted , is defined as follows. Let Then for ,
Metric space structure
Length of curves and the Riemannian distance function are defined in a way similar to the finite-dimensional case. The distance function , called the geodesic distance, is always a pseudometric (a metric that does not separate points), but it may not be a metric.[46] In the finite-dimensional case, the proof that the Riemannian distance function separates points uses the existence of a pre-compact open set around any point. In the infinite case, open sets are no longer pre-compact, so the proof fails.
- If is a strong Riemannian metric on , then separates points (hence is a metric) and induces the original topology.[citation needed]
- If is a weak Riemannian metric, may fail to separate points. In fact, it may even be identically 0.[46] For example, if is a compact Riemannian manifold, then the weak Riemannian metric on induces vanishing geodesic distance.[47]
Hopf–Rinow theorem
In the case of strong Riemannian metrics, one part of the finite-dimensional Hopf–Rinow still holds.
Theorem: Let be a strong Riemannian manifold. Then metric completeness (in the metric ) implies geodesic completeness.[citation needed]
However, a geodesically complete strong Riemannian manifold might not be metrically complete and it might have closed and bounded subsets that are not compact.[citation needed] Further, a strong Riemannian manifold for which all closed and bounded subsets are compact might not be geodesically complete.[citation needed]
If is a weak Riemannian metric, then no notion of completeness implies the other in general.[citation needed]
Remove ads
See also
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads














































































































![{\displaystyle \gamma :[0,1]\to M}](http://wikimedia.org/api/rest_v1/media/math/render/svg/0066953642fb00abb394327531cea098815cd1c8)


![{\displaystyle [0,1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)






















![{\displaystyle [0,\delta ].}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9d2de11de6feb4841f7d0c9fff9241a77e33a258)

















![{\displaystyle \nabla _{X}Y-\nabla _{Y}X=[X,Y],}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2ca63c0cb31ba4d14004adb8d8ec84cced774a8e)
![{\displaystyle [\cdot ,\cdot ]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/28dd4c22d60192519c1c12cf645b040f368db9e9)
![{\displaystyle X:[0,1]\to TM}](http://wikimedia.org/api/rest_v1/media/math/render/svg/11fcfd3cec8c7149af97f02bf8b630cee7d0dee8)

![{\displaystyle t\in [0,1]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)

![{\displaystyle f:[0,1]\to \mathbb {R} }](http://wikimedia.org/api/rest_v1/media/math/render/svg/2de6d0d4c98d4ca7ad937c772dc3e3e914b062f5)





































![{\displaystyle R(X,Y)Z=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X,Y]}Z}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6a30a969d5b599e29c8ef7fc0344b823845e5865)
![{\displaystyle [X,Y]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/94470b44d283fde62130212956058ca6b727da37)



























