Top Qs
Timeline
Chat
Perspective
Short-time Fourier transform
Fourier-related transform suited to signals that change rather quickly in time From Wikipedia, the free encyclopedia
Remove ads
The short-time Fourier transform (STFT) is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time.[1] In practice, the procedure for computing STFTs is to divide a longer time signal into shorter segments of equal length and then compute the Fourier transform separately on each shorter segment. This reveals the Fourier spectrum on each shorter segment. One then usually plots the changing spectra as a function of time, known as a spectrogram or waterfall plot, such as commonly used in software defined radio (SDR) based spectrum displays. Full bandwidth displays covering the whole range of an SDR commonly use fast Fourier transforms (FFTs).
Remove ads
Forward STFT
Summarize
Perspective
Continuous-time STFT
Simply, in the continuous-time case, the function to be transformed is multiplied by a window function which is nonzero for only a short period of time. The Fourier transform (a one-dimensional function) of the resulting signal is taken, then the window is slid along the time axis until the end resulting in a two-dimensional representation of the signal. Mathematically, this is written as:
where is the window function, commonly a Hann window or Gaussian window centered around zero, and is the signal to be transformed (note the difference between the window function and the frequency ). is essentially the Fourier transform of , a complex function representing the phase and magnitude of the signal over time and frequency. Often phase unwrapping is employed along either or both the time axis, , and frequency axis, , to suppress any jump discontinuity of the phase result of the STFT. The time index is normally considered to be "slow" time and usually not expressed in as high resolution as time . Given that the STFT is essentially a Fourier transform times a window function, the STFT is also called windowed Fourier transform or time-dependent Fourier transform.
Discrete-time STFT
In the discrete time case, the data to be transformed could be broken up into chunks or frames (which usually overlap each other, to reduce artifacts at the boundary). Each chunk is Fourier transformed, and the complex result is added to a matrix, which records magnitude and phase for each point in time and frequency. This can be expressed as:
likewise, with signal and window . In this case, m is discrete and ω is continuous, but in most typical applications the STFT is performed on a computer using the fast Fourier transform, so both variables are discrete and quantized.
The magnitude squared of the STFT yields the spectrogram representation of the power spectral density of the function:
See also the modified discrete cosine transform (MDCT), which is also a Fourier-related transform that uses overlapping windows.
Sliding DFT
If only a small number of ω are desired, or if the STFT is desired to be evaluated for every shift m of the window, then the STFT may be more efficiently evaluated using a sliding DFT algorithm.[2]
Remove ads
Inverse STFT
Summarize
Perspective
The STFT is invertible, that is, the original signal can be recovered from the transform by the inverse STFT. The most widely accepted way of inverting the STFT is by using the overlap-add (OLA) method, which also allows for modifications to the STFT complex spectrum. This makes for a versatile signal processing method,[3] referred to as the overlap and add with modifications method.
Continuous-time STFT
Given the width and definition of the window function w(t), we initially require the area of the window function to be scaled so that
It easily follows that
and
The continuous Fourier transform is
Substituting x(t) from above:
Swapping order of integration:
So the Fourier transform can be seen as a sort of phase coherent sum of all of the STFTs of x(t). Since the inverse Fourier transform is
then x(t) can be recovered from X(τ,ω) as
or
It can be seen, comparing to above that windowed "grain" or "wavelet" of x(t) is
the inverse Fourier transform of X(τ,ω) for τ fixed.
An alternative definition that is valid only in the vicinity of τ, the inverse transform is:
In general, the window function has the following properties:
- (a) even symmetry: ;
- (b) non-increasing (for positive time): if ;
- (c) compact support: is equal to zero when |t| is large.
Remove ads
Resolution issues
Summarize
Perspective
One of the pitfalls of the STFT is that it has a fixed resolution. The width of the windowing function relates to how the signal is represented—it determines whether there is good frequency resolution (frequency components close together can be separated) or good time resolution (the time at which frequencies change). A wide window gives better frequency resolution but poor time resolution. A narrower window gives good time resolution but poor frequency resolution. These are called narrowband and wideband transforms, respectively.

This is one of the reasons for the creation of the wavelet transform and multiresolution analysis, which can give good time resolution for high-frequency events and good frequency resolution for low-frequency events, the combination best suited for many real signals.
This property is related to the Heisenberg uncertainty principle, but not directly – see Gabor limit for discussion. The product of the standard deviation in time and frequency is limited. The boundary of the uncertainty principle (best simultaneous resolution of both) is reached with a Gaussian window function (or mask function), as the Gaussian minimizes the Fourier uncertainty principle. This is called the Gabor transform (and with modifications for multiresolution becomes the Morlet wavelet transform).
One can consider the STFT for varying window size as a two-dimensional domain (time and frequency), as illustrated in the example below, which can be calculated by varying the window size. However, this is no longer a strictly time-frequency representation – the kernel is not constant over the entire signal.
Examples
When the original function is:

We can have a simple example:
w(t) = 1 for |t| smaller than or equal B
w(t) = 0 otherwise
B = window
Now the original function of the Short-time Fourier transform can be changed as
Another example:
Using the following sample signal that is composed of a set of four sinusoidal waveforms joined together in sequence. Each waveform is only composed of one of four frequencies (10, 25, 50, 100 Hz). The definition of is:
Then it is sampled at 400 Hz. The following spectrograms were produced:
 |
 |
 |
 |
The 25 ms window allows us to identify a precise time at which the signals change but the precise frequencies are difficult to identify. At the other end of the scale, the 1000 ms window allows the frequencies to be precisely seen but the time between frequency changes is blurred.
Other examples:

Normally we call a Gaussian function or Gabor function. When we use it, the short-time Fourier transform is called the "Gabor transform".
Explanation
It can also be explained with reference to the sampling and Nyquist frequency.
Take a window of N samples from an arbitrary real-valued signal at sampling rate fs . Taking the Fourier transform produces N complex coefficients. Of these coefficients only half are useful (the last N/2 being the complex conjugate of the first N/2 in reverse order, as this is a real valued signal).
These N/2 coefficients represent the frequencies 0 to fs/2 (Nyquist) and two consecutive coefficients are spaced apart by fs/N Hz.
To increase the frequency resolution of the window the frequency spacing of the coefficients needs to be reduced. There are only two variables, but decreasing fs (and keeping N constant) will cause the window size to increase — since there are now fewer samples per unit time. The other alternative is to increase N, but this again causes the window size to increase. So any attempt to increase the frequency resolution causes a larger window size and therefore a reduction in time resolution—and vice versa.
Remove ads
Rayleigh frequency
As the Nyquist frequency is a limitation in the maximum frequency that can be meaningfully analysed, so is the Rayleigh frequency a limitation on the minimum frequency.
The Rayleigh frequency is the minimum frequency that can be resolved by a finite duration time window.[4][5]
Given a time window that is Τ seconds long, the minimum frequency that can be resolved is 1/Τ Hz.
The Rayleigh frequency is an important consideration in applications of the short-time Fourier transform (STFT), as well as any other method of harmonic analysis on a signal of finite record-length.[6][7]
Remove ads
Application

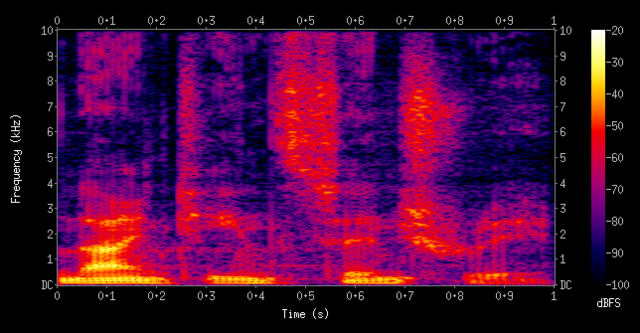
STFTs as well as standard Fourier transforms and other tools are frequently used to analyze music. The spectrogram can, for example, show frequency on the horizontal axis, with the lowest frequencies at left, and the highest at the right. The height of each bar (augmented by color) represents the amplitude of the frequencies within that band. The depth dimension represents time, where each new bar was a separate distinct transform. Audio engineers use this kind of visual to gain information about an audio sample, for example, to locate the frequencies of specific noises (especially when used with greater frequency resolution) or to find frequencies which may be more or less resonant in the space where the signal was recorded. This information can be used for equalization or tuning other audio effects.
Remove ads
Implementation
Summarize
Perspective
Original function
Converting into the discrete form:
Suppose that
Then we can write the original function into
Direct implementation
Constraints
a. Nyquist criterion (avoiding the aliasing effect):
- , where is the bandwidth of
FFT-based method
Constraint
a. , where is an integer
b.
c. Nyquist criterion (avoiding the aliasing effect):
- , is the bandwidth of
Recursive method
Constraint
a. , where is an integer
b.
c. Nyquist criterion (avoiding the aliasing effect):
- , is the bandwidth of
d. Only for implementing the rectangular-STFT
Rectangular window imposes the constraint
Substitution gives:
Change of variable n-1 for n:
Calculate by the N-point FFT:
where
Applying the recursive formula to calculate
Chirp Z transform
Constraint
so
Implementation comparison
Remove ads
See also
- Least-squares spectral analysis
- Spectral density estimation
- Time-frequency analysis
- Time-frequency representation
- Reassignment method
Other time-frequency transforms:
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads










![{\displaystyle \mathbf {STFT} \{x[n]\}(m,\omega )\equiv X(m,\omega )=\sum _{n=0}^{N-1}x[n]w[n-m]e^{-i\omega n}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/024e0023201ee3e35baa6c64c2b3402056f25e0c)
![{\displaystyle x[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/864cbbefbdcb55af4d9390911de1bf70167c4a3d)
![{\displaystyle w[n]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/2a4e3e5afc2a8c6da9020b8c6b21450959101a18)





![{\displaystyle X(\omega )=\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,d\tau \right]\,e^{-i\omega t}\,dt}](http://wikimedia.org/api/rest_v1/media/math/render/svg/339f08d24c67eb1431eab470a47cbf50dc5a882b)


![{\displaystyle =\int _{-\infty }^{\infty }\left[\int _{-\infty }^{\infty }x(t)w(t-\tau )\,e^{-i\omega t}\,dt\right]\,d\tau }](http://wikimedia.org/api/rest_v1/media/math/render/svg/6f5f84afa30959a68d8043288f64cdf358c9368e)



![{\displaystyle x(t)=\int _{-\infty }^{\infty }\left[{\frac {1}{2\pi }}\int _{-\infty }^{\infty }X(\tau ,\omega )e^{+i\omega t}\,d\omega \right]\,d\tau .}](http://wikimedia.org/api/rest_v1/media/math/render/svg/6a28e00f9132204db58dca60c49d0e473398777a)




































 ,
,  ...
...