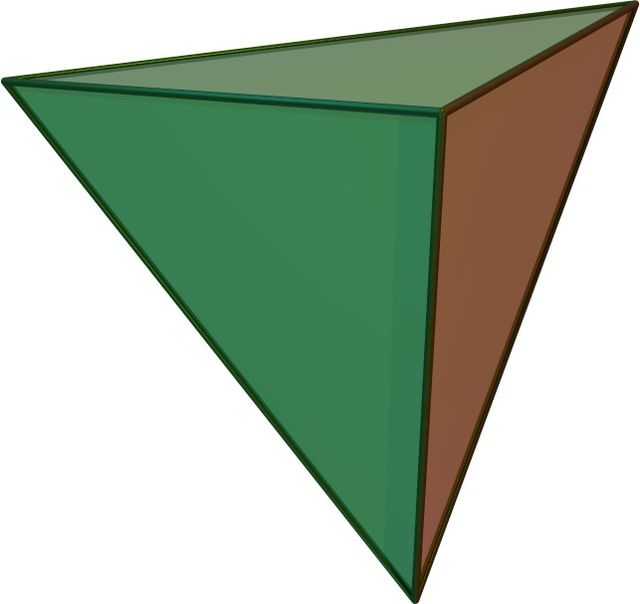
Tetrahedron
Polyhedron with 4 faces / From Wikipedia, the free encyclopedia
Dear Wikiwand AI, let's keep it short by simply answering these key questions:
Can you list the top facts and stats about Tetrahedral?
Summarize this article for a 10 year old
In geometry, a tetrahedron (pl.: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertices. The tetrahedron is the simplest of all the ordinary convex polyhedra.[1]
| Regular tetrahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Platonic solid |
| Elements | F = 4, E = 6 V = 4 (χ = 2) |
| Faces by sides | 4{3} |
| Conway notation | T |
| Schläfli symbols | {3,3} |
| h{4,3}, s{2,4}, sr{2,2} | |
| Face configuration | V3.3.3 |
| Wythoff symbol | 3 | 2 3 | 2 2 2 |
| Coxeter diagram | |
| Symmetry | Td, A3, [3,3], (*332) |
| Rotation group | T, [3,3]+, (332) |
| References | U01, C15, W1 |
| Properties | regular, convexdeltahedron |
| Dihedral angle | 70.528779° = arccos(1⁄3) |
 3.3.3 (Vertex figure) |
 Self-dual (dual polyhedron) |
 Net | |

The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex.
The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid".
Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.[1]
For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere (the insphere) tangent to the tetrahedron's faces.[2]



